O termo recorrência é definido, cientificamente, como:
O caráter do que é recorrente; retorno, repetição.
Oxford Languades
Na computação, recorrências costumam aparecer em procedimento de natureza recursiva, arbitrados por critérios de parada que os impedem de permanecer em looping infinitos de operação. Uma recorrência é uma equação ou desigualdade que descreve uma função em termos de seu valor em entradas menores.
Recursividade
O termo recursividade é definido, cientificamente, como:
A propriedade daquilo que se pode repetir um número indefinido de vezes.
Oxford Languades
Na computação, um procedimento é recursivo quando chama a si mesmo, direta ou indiretamente. A recursividade permite descrever algoritmos de forma mais clara e concisa, especialmente nos problemas recursivos por natureza ou que utilizam estruturas recursivas.
Os problemas de natureza recursiva são modelados computacionalmente através de funções recursivas que representam as recorrências por meio de algoritmos computacionais. Normalmente, as funções recursivas são divididas em duas partes:
- a condição de parada, que evita loops infinitos;
- a chamada recursiva, que pode ser direta ou indireta.
Dado o algoritmo para o cálculo fatorial de um número em sua implementação recursiva em C:
Observa-se que a condição de parada consiste no condicional presente da linha 2 a linha 4. Já a chamada recursiva direta esta presente da linha 5 a linha 7.
Alguns exemplos de problemas que utilizam de estruturas recursivas são apresentados a seguir:
Quando uma chamada de função é feita, um registro de ativação é alocado na pilha de dados de execução do programa na memória do computador. O registro de ativação guarda dois dados:
- os parâmetros e as variáveis locais da função;
- o ponto de retorno da função.
Desta forma, o custo em espaço de memória aumenta a cada chamada recursiva da função. Logo, se deve atentar ao custo de tempo (período de execução) e ao custo de espaço (memória) na análise de algoritmos implementados recursivamente.
Assim, a eficiência de um algoritmo depende do balanço entre os custos de tempo e espaço para a sua execução e os recursos computacionais disponíveis. Estes custos vão depender da implementação adotada pelo algoritmo e da natureza do problema.
Geralmente, o custo de tempo fica mais evidente nos algoritmos em sua implementação recursiva e o custo de espaço em sua implementação iterativa. Contudo, a recursividade nem sempre é a melhor solução, mesmo quando a definição matemática é feita em termos recursivos.
Também é possível observar esta realidade no estudo da sequência de Fibonacci, em que sua definição é a própria implementação do algoritmo que a representa. Seu algoritmo/definição em sua implementação recursiva em C é:
Da implementação recursiva observa-se que o algoritmo não é apropriado para valores de $n$ muito elevado uma vez que sua execução acumula um custo de espaço a cada chamada recursiva e um custo de tempo exponencial para o termino de sua execução:
fibonacci(n-1)+fibonacci(n-2)
fibonacci(n-1)+fibonacci(n-2)+fibonacci(n-1)+fibonacci(n-2)
fibonacci(n-1)+fibonacci(n-2)+fibonacci(n-1)+fibonacci(n-2)+fibonacci(n-1)+fibonacci(n-2)
$\cdot$
$\cdot$
$\cdot$
onde:
- $F(n-1)$ e $F(n-2)$ são computados independentemente e repetidas vezes;
- o número de chamadas recursivas é igual a posição do número na sequência $n$;
- o custo de espaço e tempo para o cálculo de $f(n)$ são de complexidade exponencial $O(c^n)$, $c>1$.
Portanto, o uso incorreto da recursividade na implementação de um algoritmo pode levar a sua ineficiência em relação as outras possibilidades. Assim, apesar da implementação recursiva apresentar o funcionamento de um algoritmo de maneira mais clara, esta clareza pode custar a ineficiência de sua execução, cabendo ao desenvolvedor realizar a análise de sua complexidade antes de adotá-la em suas aplicações.
Seguindo a análise do algoritmo de Fibonacci, temos que sua implementação iterativa em C é:
em que o custo de espaço é $O(1)$ e o custo de tempo é de $O(n)$.
Logo, é recomendável o uso da implementação iterativa do algoritmo de Fibonacci pois sua implementação recursiva tem complexidade exponencial e esta complexidade não é passível de controle de execução para valores grandes de $n$ pelos computadores atuais.
Cabe enfatizar que nem sempre é possível implementar uma forma iterativa de um algoritmo recursivo.
Existem alguns casos em que a recursividade pode ser aplicada. São eles, quando:
- o algoritmo for do tipo dividir para conquistar (quicksort, algoritmos de busca etc);
- o algoritmo for de caminhamento em árvores;
- o algoritmo for do tipo busca exaustiva.
Equações de Recorrência
Equações de recorrência são uma maneira de definir uma função por uma expressão envolvendo a mesma função.
Quando um algoritmo contém uma chamada recursiva, seu tempo de execução pode frequentemente ser descrito por equações de recorrência. A ferramenta principal na análise de algoritmos recursivos não é uma somatória, mas um tipo especial de equação chamada relação de recorrência.
Em uma relação de recorrência cada procedimento recursivo é associado a uma função de complexidade $T(n)$ desconhecida, onde $n$ mede o tamanho dos argumentos para o procedimento.
Dado um algoritmo aleatório que inspeciona os elementos de um vetor implementado em sua forma recursiva em C:
É possível observar que, de alguma forma, o algoritmo permite descartar $2/3$ dos elementos e fazer uma chamada recursiva sobre $1/3$ do vetor original.
Assim, para o caso base da recursão:
- O custo da linha $2$ é $\Theta(1)$;
- O custo da linha $3$ é $\Theta(1)$.
Para o caso geral da recursão:
- O custo da linha $6$ é $\Theta(n)$;
- A linha $7$ é onde a própria função é chamada em um conjunto reduzido $T(n/3)$.
Logo, a relação de recorrência para o algoritmo de inspeção implementado em sua forma recursiva é:
| $ \displaystyle T(n) = \left \{ \begin{matrix} 1 \text{, se } n \leq 1 \qquad\qquad\qquad\,\,\, \\ T(n/3)+n \text{, caso contrário} \end{matrix} \right. $ | (1) |
Métodos de Resolução das Equações de Recorrência
Três métodos para a resolução de equações de recorrência são:
- Método de substituição (ou Expandir, Conjecturar e Verificar): resolve a maioria das equações, exceto aquelas cuja soluções são matematicamente inviáveis;
- Método de expansão da árvore de recorrência: bastante intuitivo, mas pouco formal;
- Teorema mestre: cobre muitos casos, mas não todos.
O Método da Substituição (ou Expandir, Conjecturar e Verificar)
Expandir consiste em tentar imaginar como será a próxima iteração da recorrência, ou seja, usa repetidamente a recorrência para expandir a expressão a partir do n-ésimo termo até o caso base. Como, por exemplo, dada a equação (1), assumindo que $ n > 1 $, temos que:
| $ \displaystyle T(n) = T(n/3)+n $ | (2) |
Assumindo que $ n=n/3 $ na próxima iteração da recorrência e assim sucessivamente, substituindo em (2), temos que:
| $ T(n) = T(n/3)+n $ $ T(n/3) = T( {n/3}/3 )+n/3 $ $ T( {n/3}/3 ) = T( {{n/3}/3}/3 ) + {n/3}/3 $ $ \vdots $ $ T( {n/3}/3 \cdots /3 ) = T( {{n/3}/3}/3 \cdots /3 ) + {n/3}/3 \cdots /3 $ | (3) |
Desta forma, podemos observar que a substituição recursiva de $n$ por $n/3$ implica que, em algum momento, $n \leq 1$, ou seja, a recorrência $(1)$ tenderá ao seu caso base:
|
$ T(n)$ $ T(n/3)$ $ T( {n/3}/3 )$ $ T( {n/3}/3 \cdots /3 )$ $ \vdots $ $T(1)=1$ | (4) |
Assim, podemos representar (3) por:
|
$ T(n)-T(n/3) = n $ $ T(n/3)-T( {n/3}/3 ) = n/3 $ $ T( {n/3}/3 )-T( {{n/3}/3}/3 ) = {n/3}/3 $ $ \vdots $ $ T( {n/3}/3 \cdots /3 )-T( {{n/3}/3}/3 \cdots /3 ) = {n/3}/3 \cdots /3 $ $ T(1) = 1 $ | (5) |
Somando os termos da recorrência (5), temos que:
| $ T(n) = n + n/3 + {n/3}/3 + \cdots + {{n/3}/3}/3 \cdots /3 + 1 $ | (6) |
Isolando $n$, temos que:
| $ T(n) = n \left ( 1 + 1/3 + {1/3}/3 + \cdots + {{1/3}/3}/3 \cdots /3 \right ) + 1 $ | (7) |
Reescrevendo, temos que:
| $ \displaystyle T(n)=n \sum_{i=0}^{\infty}\left ( \frac{1}{3} \right )^i+1 $ | (8) |
Dá somatória, podemos observar que a fórmula resultante representa a soma de uma série geométrica de razão $1/3$ multiplicada por $n$ e adicionada de $T( {{n/3}/3}/3 \cdots /3 )$, que é menor ou igual a 1. Então, aplicando a solução (a.3) na equação (8), temos que:
| $ \displaystyle T(n)=n \left ( \frac{1}{1-1/3} \right ) +1 $ | (9) |
Reescrevendo, temos que:
| $ \displaystyle T(n)=\frac{3n}{2}+1 $ | (10) |
Portanto, a complexidade de $T(n)$ é $\Theta (n) $. Conjecturar a solução, neste caso, consiste no resultado da expansão, ou seja, na obtenção da equação (10) de complexidade $\Theta (n) $. Consequentemente, verificar consiste em provar, por indução, a solução (10) obtida.
Outro exemplo, dada a relação de recorrência (11):
| $ \displaystyle T(n) = \left \{ \begin{matrix} 2 \text{, se } n < 2 \qquad\qquad\qquad\,\,\, \\ 2T(n-1) \text{, caso contrário} \end{matrix} \right. $ | (11) |
Assumindo que $ n \geq 2 $, temos que:
| $ \displaystyle T(n)=2T(n-1) $ | (12) |
Assumindo que $ n=n-1 $ na próxima iteração da recorrência e assim sucessivamente, substituindo em (12), temos que:
|
$ T(n)=2T(n-1) $ $ T(n-1) = 2[2T(n-1-1)] $ $ T(n-1-1) = 2[2[2T(n-1-1-1)]] $ $ \vdots $ $ T( n-1-1 \cdots -1 ) = 2[2[2[\cdots 2T(n-1-1-1 \cdots -1)]]] $ | (13) |
Reescrevendo, temos que:
|
$ T(n)=2T(n-1) $ $ T(n-1) = 2^2T(n-2) $ $ T(n-2) = 2^3T(n-3) $ $ \vdots $ $ T( n-2 \cdots -1 ) = 2^3\cdots 2T(n-3 \cdots -1)]]] $ | (14) |
Analisando o padrão, conjecturamos que, após $k$ expansões, a equação tem a forma:
| $ T(n)=2^iT(n-i) $ | (15) |
A expansão tem que parar quando $n-i=1$, ou seja, quando $k=n-1$. Nesse ponto temos:
| $ T(n)=2^{n-1}T(n-(n-1)) $ | (16) |
Reescrevendo, temos que:
| $ T(n)=2^{n-1}T(1) $ | (17) |
Da recorrência (11), temos que:
| $ T(n)=2^{n-1}2 $ | (18) |
Reescrevendo novamente, temos que:
| $ T(n)=2^n $ | (19) |
Portanto, a complexidade de $T(n)$ é $\Theta (2^n) $. Conjecturar a solução, neste caso, consiste no resultado da expansão, ou seja, na obtenção da equação (19) de complexidade $\Theta (2^n) $. Consequentemente, verificar consiste em provar, por indução, a solução (19) obtida:
i) É possível observar que a base da indução é $T(1)=2^1$ é verdadeira pelo caso base da definição recursiva (11).
ii) Supondo que $T(k)=2^k$, queremos provar que $T(k+1)=2^{k+1}$:
| $ T(k+1)=2T(k) $ | (20) |
| $ T(k+1)=2(2^k) \,\, $ | (21) |
| $ T(k+1)=2^{k+1} \,\,\, $ | (22) |
Portanto, fica provada a relação de recorrência (11).
O Método de Expansão da Árvore de Recorrência
O método da expansão da árvore de recorrência consiste na representação da recorrência por meio do desenho de um diagrama de árvore cujo os nós representam os tamanhos dos problemas como, por exemplo, dada a relação de recorrência (21):
| $ \displaystyle T(n) = \left \{ \begin{matrix} \Theta(1) \qquad\quad\,\, \text{, se } n = 1 \\ 2T(n/2)+n \text{, se } n > 1 \end{matrix} \right. $ | (23) |
No primeiro passo da recursão, temos:
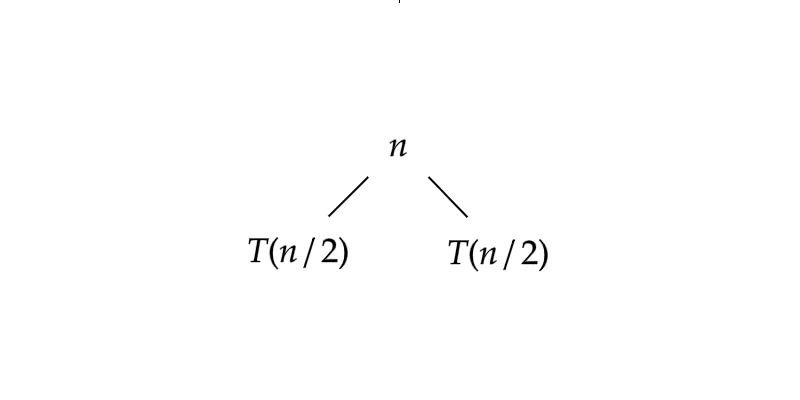
No próximo passo recursivo, temos:
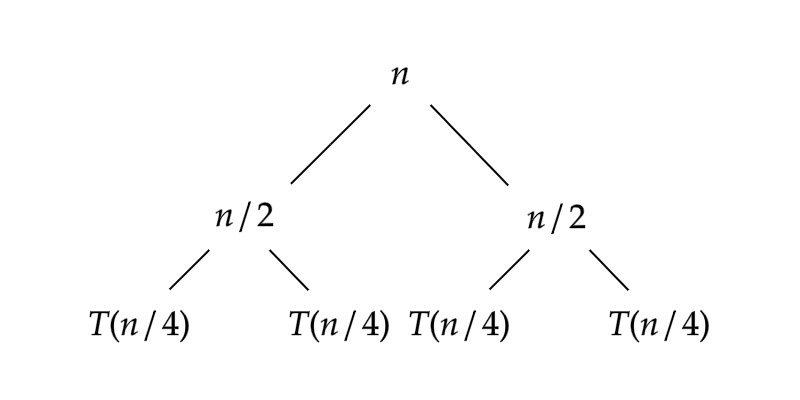
Intuitivamente, na n-ésima recurção, temos:
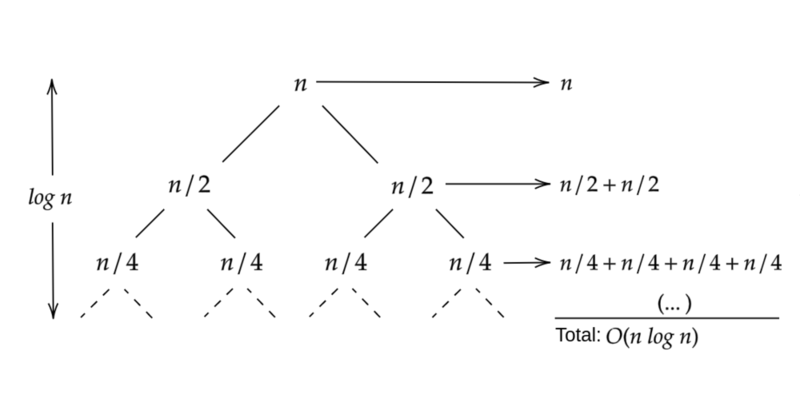
Cada nível $i$ contém todos os subproblemas de profundidade $i$.
No traço do diagrama de árvore dois aspectos importantes são:
- a altura da árvore;
- o número de passos executados.
Sendo a solução da recorrência igual a soma de todos os níveis da árvore.
O Método Mestre
O método mestre fornece uma receita para a solução de equações de recorrências lineares de primeira ordem na forma:
$ T(n)=a \cdot T(n/b)+f(n) $
onde $a \geq 1$ e $b > 1$ são constantes e $f(n)$ é uma função assintoticamente positiva e $n/b$ pode ser $\left \lfloor n/b \right \rfloor$ ou $\left \lceil n/b \right \rceil$.
Nestas circunstâncias, existem três casos de prova da equação de recorrência para a obtenção da solução, dados por:
- Se $f(n)=O \left ( n^{ \displaystyle (\log_b a)-\epsilon } \right ) $ para alguma constante $\epsilon > 0$ então $T(n)=\Theta \left ( n^{\displaystyle \log_b a} \right ) $;
- Se $f(n)=\Theta \left ( n^{ \displaystyle \log_b a } \right ) $ então $T(n)=\Theta \left ( n^{\displaystyle \log_b a} \cdot \log n \right ) $;
- Se $f(n)=\Omega \left ( n^{ \displaystyle (\log_b a)+\epsilon } \right ) $ para alguma constante $\epsilon > 0$, e se $a \cdot f(n/b) \leq c \cdot f(n)$ para alguma constante $c<1$ e $n$ suficientemente grande, então $T(n)=\Theta(f(n))$.
Nos casos 1 e 3, $\epsilon$ é um artificio matemático que consiste em realizar um pequeno ajuste na equação, para sua simplificação. Para isso, é adorado um valor arbitrado $\epsilon$ tal que a equação de recorrência seja simplificada nestes dois casos.
Assim, na aplicação do método mestre a equação de recorrência deve satisfazer uma de suas três condições. Caso contrário será necessário utilizar o método da substituição.
Exemplo 01: Dada a equação de recorrência $T(n)=9T(n/3)+n$.
Pelo caso 1, para $a=9$ e $b=3$ temos:
$f(n)=O \left ( n^{ \displaystyle (\log_b a)-\epsilon } \right )$
$ n \leq c \cdot n^{ \displaystyle (\log_3 9)-\epsilon }$
$ n \leq c \cdot n^{ \displaystyle 2-\epsilon } \qquad\,\,\, $
Adotando $\epsilon=1$:
$ n \leq c \cdot n \qquad\qquad\,\,\, $
A inequação se satisfaz. Portanto, pelo caso 1, a solução da recorrência é dada por:
$T(n)=\Theta(n^2)$
Exemplo 02: Dada a equação de recorrência $T(n)=9T(2n/3)+1$.
Pelo caso 1, para $a=1$ e $b=3/2$ temos:
$f(n)=O \left ( n^{ \displaystyle (\log_b a)-\epsilon } \right )$
$ 1 \leq c \cdot n^{ \displaystyle (\log_{1,5} 1)-\epsilon }$
$ 1 \leq c \cdot n^{ \displaystyle 0-\epsilon } \qquad\quad\, $
Neste caso, a inequação se mostra um absurdo. Portanto, a obtenção da solução da recorrência pelo caso 1 falhou.
Pelo caso 2, para $a=1$ e $b=3/2$ temos:
$f(n)=\Theta \left ( n^{ \displaystyle \log_b a } \right )$
$ 1 = c \cdot n^{ \displaystyle \log_{1,5} 1 }$
$ 1 = c \cdot n^0 \qquad\,\, $
$ 1 = c \cdot 1 \qquad\,\,\,\,\, $
A equação se satisfaz. Portanto, pelo caso 2, a solução da recorrência é dada por:
$T(n)=\Theta(\log n)$
Exemplo 03: Dada a equação de recorrência $T(n)=3T(n/4)+n \log n$.
Pelo caso 1, para $a=3$ e $b=4$ temos:
$f(n)=O \left ( n^{ \displaystyle (\log_b a)-\epsilon } \right )$
$ n \log n \leq c \cdot n^{ \displaystyle (\log_4 3)-\epsilon }$
Adotando $\epsilon=\log_4 3/2$:
$ n \log n \leq c \cdot n^{ \displaystyle \log_4 2 }$
$ n \log n \leq c \cdot n^{ 0,5 } \quad\,\, $
Neste caso, a inequação se mostra um absurdo. Portanto, a obtenção da solução da recorrência pelo caso 1 falhou.
Pelo caso 2, para $a=3$ e $b=4$ temos:
$f(n)=\Theta \left ( n^{ \displaystyle \log_b a } \right )$
$ n \log n = c \cdot n^{ \displaystyle \log_4 3 }$
$ n \log n = c \cdot n^{ 0,79 } \quad $
Neste caso, a inequação se mostra um absurdo. Portanto, a obtenção da solução da recorrência pelo caso 2 falhou.
Pelo caso 3, para $a=3$ e $b=4$ temos:
$f(n)=\Omega \left ( n^{ \displaystyle (\log_b a)+\epsilon } \right ) $
$ n \log n \geq c \cdot n^{ \displaystyle (\log_4 3)+\epsilon } $
Adotando $\epsilon=\log_4 3/4$:
$ n \log n \geq c \cdot n^1 $
e
$ a \cdot f(n/b) \Rightarrow 3 \cdot (n/4) \log (n/4) \leq (3/4) \cdot n \log n $
As inequações se satisfazem. Portanto, pelo caso 3, a solução da recorrência é dada por:
$T(n)=\Theta(n\log n)$
Apêndice: Algumas Séries Úteis
Séries Aritméticas
| $ \displaystyle \sum_{i=0}^{n}i=\frac{n\left ( n+1 \right )}{2}\equiv O\left ( n^2 \right ) \qquad\qquad $ | (a.1) |
| $ \displaystyle \sum_{i=0}^{n}i^2=\frac{n\left ( n+1 \right )\left ( n+2 \right )}{6}\equiv O\left ( \frac{n^3}{3} \right ) $ | (a.2) |
Séries Geométricas
| $ \displaystyle \sum_{i=0}^{\infty} x^i=\frac{1}{1-x} $ | (a.3) |
| $ \displaystyle \sum_{i=0}^{n}\frac{i}{2^i}=2 \qquad\quad\, $ | (a.4) |
Séries Harmônicas
| $ \displaystyle \sum_{i=1}^{n}\frac{1}{i}=\ln n+O(1)\equiv O\left ( \ln n \right ) $ | (a.5) |
Referências
- PIVA JÚNIOR, Dilermando (et al). Estrutura de dados e técnicas de programação. 1. ed. Rio de Janeiro, RJ: Campus, 2014. 399 p. ISBN: 9788535274370.
- CORMEN, Thomas H et al. Algoritmos: teoria e prática. Rio de Janeiro: Elsevier, 926 p. ISBN: 9788535236996.
- TOSCANI, Laira Vieira; VELOSO, Paulo A. S. Complexidade de algoritmos: análise, projeto e métodos. 3. ed. Porto Alegre: Bookman, 2012. 261 p. (Série livros didáticos informática UFRGS, 13) ISBN: 9788540701380.
- ASCENCIO, Ana Fernanda Gomes. Estruturas de dados: algoritmos, análise da complexidade e implementações em Java e C/C++. São Paulo: Pearson, c2010. 432 p. ISBN: 9788576052216, 978857605816.
- BRASSARD, Gilles; BRATLEY, Paul. Fundamentals of algorithmics. Englewood Cliffs: Prentice Hall, c1996. xx, 524 p. ISBN: 0133350681.





