A sequência de Fibonacci é uma sequência de números inteiros de construção peculiar. Embora tenha sido descrita anteriormente na matemática indiana, já em 200 a.C. no trabalho de Pingala (300 a.C) sobre a enumeração de possíveis padrões de poesia sânscrita formados a partir de sílabas de dois comprimentos, a sequência tem este nome em homenagem a Leonardo Fibonacci (1170-1250), que introduziu a sequência na matemática da Europa Ocidental em seu livro Liber Abaci (1202), mas depois de alguns parágrafos sobre coelhos reprodutores, Leonardo de Pisa não tornou a mencionar a sequência. Na verdade, foi esquecido em grande parte até o século XIX, quando os matemáticos trabalharam mais sobre as propriedades matemáticas da sequência. Em 1877, o matemático francês Édouard Lucas (1842-1891) chamou oficialmente o problema do coelho de “a sequência de Fibonacci”. Os onze primeiros elementos desta sequência são:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
onde cada elemento $f_n$ é calculado, sequencialmente, pela soma de seus dois antecessores, tal como:
| Rótulo | Operação | Sequência de Fibonacci |
|---|---|---|
| $f_0$ | – | $0$ |
| $f_1$ | – | $1$ |
| $f_2$ | $0+1$ | $1$ |
| $f_3$ | $1+1$ | $2$ |
| $f_4$ | $1+2$ | $3$ |
| $f_5$ | $2+3$ | $5$ |
| $f_6$ | $3+5$ | $8$ |
| $f_7$ | $5+8$ | $13$ |
| $f_8$ | $8+13$ | $21$ |
| $f_9$ | $13+21$ | $34$ |
| $f_{10}$ | $21+34$ | $55$ |
| $\vdots$ | $\vdots$ | $\vdots$ |
| $f_n$ | $f_{n-2}+f_{n-1}$ | – |
Da observação de seu comportamento a partir do elemento $f_0$ temos que:
$ \left \{ \begin{matrix}
f_0 = 0 \qquad\qquad\,\,\, \\
f_1 = 1 \qquad\qquad\,\,\, \\
f_n=f_{n-1}+f_{n-2}
\end{matrix} \right. $
onde $ n = \{1,2,3,4,…\} $ é o conjunto dos números inteiros não negativos $ \mathbb{Z_+} $ que representa a contagem dos elementos da sequência.
Da observação de seu comportamento a partir do elemento $f_3$ temos que:
$ f_{3}=f_1+f_2 \Rightarrow f_{1+2}=f_1+f_{1+1} \qquad\qquad\qquad\,\,\,\, $
$ f_{2+2}=f_2+f_{2+1} $
$ f_{3+2}=f_3+f_{3+1} $
$ f_{\vdots+2}=f_\vdots+f_{\vdots+1} $
$ f_{n+2}=f_n+f_{n+1} $
Desta forma, a sequência Fibonacci também pode ser definida como:
$ \left \{ \begin{matrix}
f_1 = 1 \qquad\,\,\, \\
f_2 = 1 \qquad\,\,\, \\
f_{n+2}=f_n+f_{n+1}
\end{matrix} \right. $
onde $ n = \{1,2,3,4,…\} $ é o conjunto dos números inteiros positivos $ \mathbb{Z_+} $ que representa a contagem dos elementos da sequência.
Ao representar a sequência de Fibonacci em retângulos com largura e comprimento sendo pares interligados desta sequência e dispô-los de maneira geométrica é possível traçar os retângulos de ouro (Figura 1).
Figura 1 – Retângulos de ouro formado por conjuntos pares da sequência de Fibonacci.
Fonte: Autor.
Ao dividir os retângulos de ouro por quadrados consoantes em largura a sequência e dispô-los de maneira geométrica, é possível traçar uma espiral perfeita pela ligação de seus vértices (Figura 2).
Figura 2 – Espiral logarítmica formada pela sequência de Fibonacci.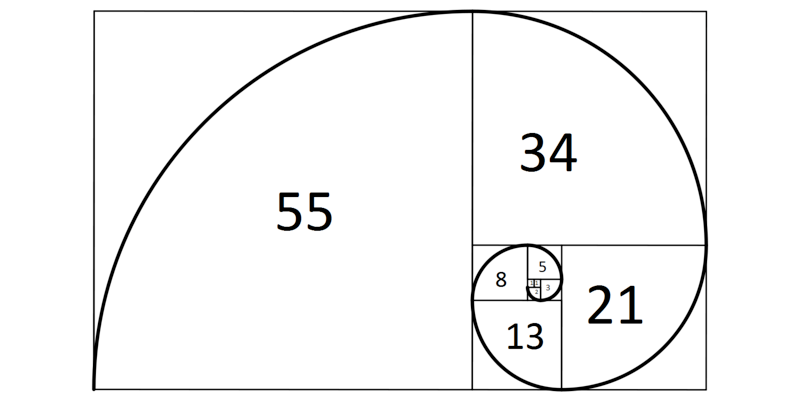 
Fonte: Autor.
Ao desenhar círculos nestes quadrados teremos o esboço do design gráfico das circunferências usadas para a criação de logos de diversas empresas bastante conhecidas como o android, apple, nubank, twitter, ubuntu etc (Figura 3).
Figura 3 – Esboço do design gráfico de diversas logos formada pela sequência de Fibonacci.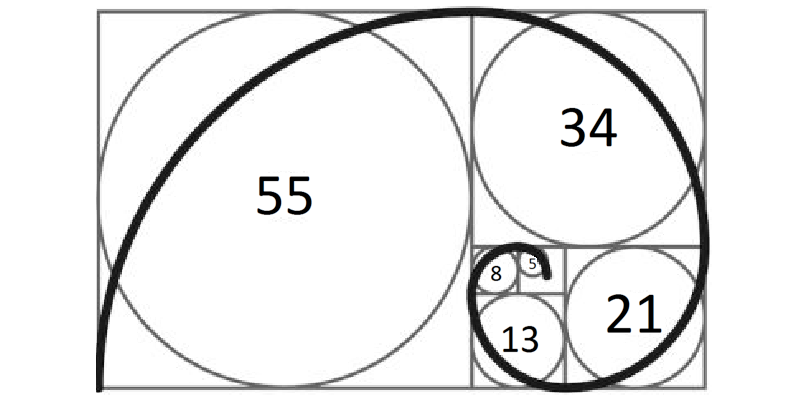
Fonte: Autor.
Esta espiral também aparece em diversos elementos da natureza, independente de sua escala (Figura 6).
A Proporção Áurea
A proporção áurea ou número de ouro é uma constante numérica equivalente ao número 1,618. Em 1753, o matemático escocês Robert Simson (1687-1768) descobriu a divisão entre os elementos da sequência de Fibonacci e os seus antecessores produziam um quocientes que oscilam próximos a 1,618, até a sua convergência. Essa constante é representada pela letra grega $\varphi$. As dez primeiras operações sobre a sequência de Fibonacci são:
$ \frac{1}{1} $, $ \frac{2}{1} $, $ \frac{3}{2} $, $ \frac{5}{3} $, $ \frac{8}{5} $, $ \frac{13}{8} $, $ \frac{21}{13} $, $ \frac{34}{21} $, $ \frac{55}{34} $, $ \cdots $
onde cada elemento $\varphi_n$ é calculado, sequencialmente, tal como:
| Sequência de Fibonacci | Rótulo | Proporção Aurea | Quociente |
|---|---|---|---|
| $0$ | $\varphi_0$ | – | – |
| $1$ | $\varphi_1$ | $1/0$ | – |
| $1$ | $\varphi_2$ | $1/1$ | $1$ |
| $2$ | $\varphi_3$ | $2/1$ | $2$ |
| $3$ | $\varphi_4$ | $3/2$ | $1,5$ |
| $5$ | $\varphi_5$ | $5/3$ | $1,6667$ |
| $8$ | $\varphi_6$ | $8/5$ | $1,6$ |
| $13$ | $\varphi_7$ | $13/8$ | $1,625$ |
| $21$ | $\varphi_8$ | $21/13$ | $1,6154$ |
| $34$ | $\varphi_9$ | $34/21$ | $1,619$ |
| $55$ | $\varphi_{10}$ | $55/34$ | $1,6176$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $f_n$ | $\varphi_n$ | $f_{n} / f_{n-1}$ | – |
Esta proporção também pode ser observada nas diagonais dos quadrados formados pela sequência de Fibonacci (Figura 4).
Figura 4 – Diagonais dos quadrados formadas pela sequência de Fibonacci.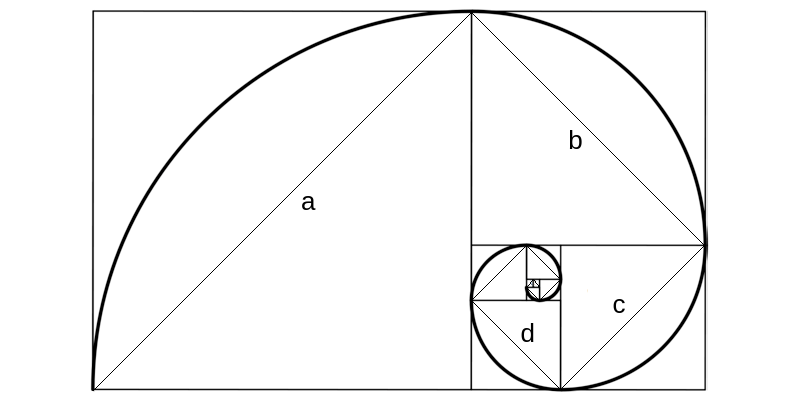
Fonte: Autor.
Matematicamente,
$ \displaystyle \varphi \approx \frac{a+b}{a} \approx \frac{b+c}{b} \approx \frac{c+d}{c} \approx 1,618 $
Refletindo sobre a natureza que nos cerca, o número de ouro não só representa o crescimento da população de coelhos, mas da evolução da natureza. A proporção áurea, sua funcionalidade e onipresença surpreendente na natureza continuou a intrigar a humanidade sobre sua importância como uma das características fundamentais do universo séculos após os estudos de Fibonacci, especialmente quando se fala em crescimento e proporção, conferindo um resultado mais harmonioso.
O ser humano tende a reproduzir uma aproximação da proporção áurea ou uma aproximação dela, mesmo quando não propositalmente, o que a faz presente na criação de modelagens computacionais, artefatos visuais e inventos esteticamente admiráveis. A prova disso é sua utilização recorrente na arte, desde as pinturas renascentistas, quando se buscava o ideal de perfeição, como na “Mona Lisa” de Leonardo da Vinci (1452-1519), “O Nascimento de Vênus” de Sandro Botticelli (1445-1510) até as obras modernas, como o “O Sacramento da Última Ceia” de Salvador Dalí (1904-1989) e as artes modernas como nos algoritmos computacionais, nas animações, na arquitetura, nos designs, no mercado financeiro, no tamanho dos outdoors, no tamanho dos cartões de créditos, entre outros (Figura 5).
Figura 5 – Proporção áurea presente na atividade humana.
(a) O nascimento de Vênus, de Botticelli.
(b) Monalisa, de Leonardo Da Vinci.
(c) Templo de Partenon, Grécia.
(d) Logomarcas.
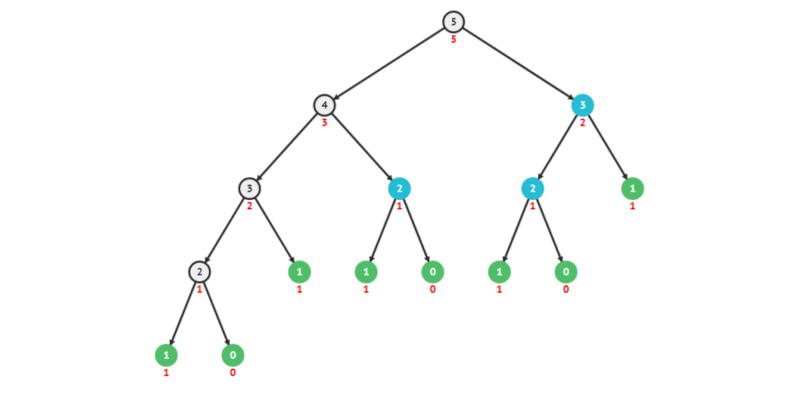(e) Grafo das chamadas recursivas da função de Fibonacci.
(f) Cartões de crédito.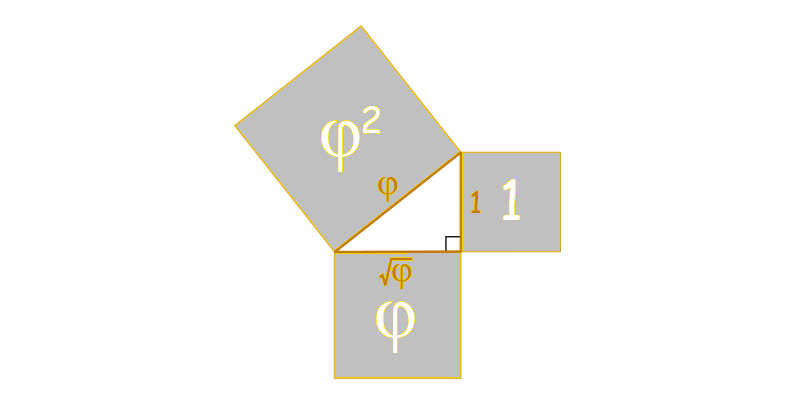
(g) Triângulo de Pitágoras.
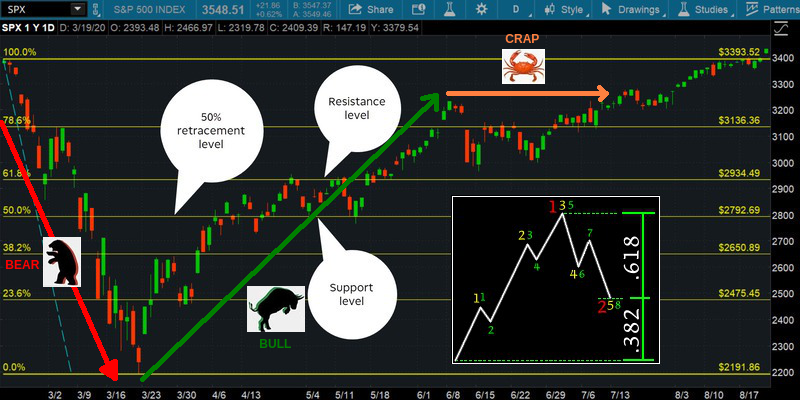
(h) Gama de níveis de retrocesso de Fibonacci. Fonte: thinkorswim® platform from TD Ameritrade.
Fonte: Autor.
Contudo, esse número não se restringe somente à sequência de Fibonacci e a engenhosidade humana. Ela também está nas espirais da natureza, nas galáxias, nos furações, nas ondas do oceano, nas conchas do mar, no crescimento da população de animais, no crescimento de plantas, nas partes do corpo humano, independente de sua escala (Figura 6).
Figura 6 – Proporção áurea presente na natureza.
(a) Braços orbitais da Via Láctea.
(b) Furação Sandy.
(c) Ondas no oceano.
(d) Concha de um molusco chamado Náutilus.
(e) Reprodução de coelhos.
(f) A quantidade de galhos em diferentes níveis de uma árvore.
(g) A quantidade necessária de folhas a dar uma volta ao caule em grande parte das espécies vegetais.
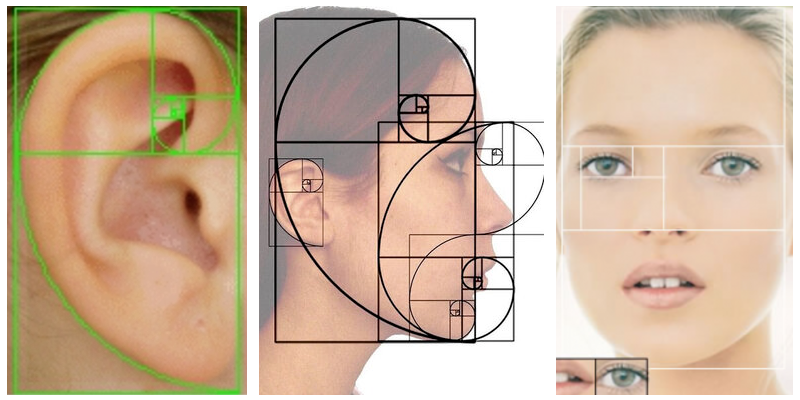
(h) A face humana.
Fonte: Autor.
O algoritmo para a geração da sequência de Fibonacci em sua implementação iterativa em C é:
O algoritmo para a geração da sequência de Fibonacci em sua implementação recursiva em C é:
Soma dos Elementos
A soma dos $n$ elementos da sequência de Fibonacci é calculada por:
$ \displaystyle f_n = \frac{ \displaystyle { \left ( \frac{1+\sqrt{5}}{2} \right ) }^n-{ \left ( \frac{1-\sqrt{5}}{2} \right ) }^n}{\sqrt{5}} $
Prova: Pela hipótese de indução, a fórmula fechada funciona para $n=k$ e também para $n=k+1$, onde $ k $ é o conjunto dos números inteiros positivos $ \mathbb{Z_+^*} $.
$ f_{k+2}=f_k+f_{k+1} $
Substituindo $f_k$ e $f_{k+1}$, temos:
$ \displaystyle f_{k+2} = \frac{ \displaystyle { \left ( \frac{1+\sqrt{5}}{2} \right ) }^k-{ \left ( \frac{1-\sqrt{5}}{2} \right ) }^k}{\sqrt{5}} + \frac{ \displaystyle { \left ( \frac{1+\sqrt{5}}{2} \right ) }^{k+1}-{ \left ( \frac{1-\sqrt{5}}{2} \right ) }^{k+1}}{\sqrt{5}} $
$ \displaystyle f_{k+2} = \frac{ \displaystyle { { \left ( \frac{1+\sqrt{5}}{2} \right ) }^k \cdot \left ( 1 + \frac{1+\sqrt{5}}{2} \right ) }-{ { \left ( \frac{1-\sqrt{5}}{2} \right ) }^k \cdot \left ( 1 + \frac{1-\sqrt{5}}{2} \right ) } }{\sqrt{5}} \,\,\,\, $
$ \displaystyle f_{k+2} = \frac{ \displaystyle { { \left ( \frac{1+\sqrt{5}}{2} \right ) }^k \cdot \left ( \frac{3+\sqrt{5}}{2} \right ) }-{ { \left ( \frac{1-\sqrt{5}}{2} \right ) }^k \cdot \left ( \frac{3-\sqrt{5}}{2} \right ) } }{\sqrt{5}} \qquad\qquad $
Substituindo $f_{k+2}$, temos:
$ \displaystyle \frac{ \displaystyle { { \left ( \frac{1+\sqrt{5}}{2} \right ) }^{k+2} }-{ { \left ( \frac{1-\sqrt{5}}{2} \right ) }^{k+2} } }{\sqrt{5}} = \frac{ \displaystyle { { \left ( \frac{1+\sqrt{5}}{2} \right ) }^k \cdot \left ( \frac{3+\sqrt{5}}{2} \right ) }-{ { \left ( \frac{1-\sqrt{5}}{2} \right ) }^k \cdot \left ( \frac{3-\sqrt{5}}{2} \right ) } }{\sqrt{5}} $
$ \displaystyle \frac{ \displaystyle { { \left ( \frac{1+\sqrt{5}}{2} \right ) }^k \cdot { \left ( \frac{1+\sqrt{5}}{2} \right ) }^2 }-{ { \left ( \frac{1-\sqrt{5}}{2} \right ) }^k \cdot { \left ( \frac{1-\sqrt{5}}{2} \right ) }^2 } }{\sqrt{5}} = \frac{ \displaystyle { { \left ( \frac{1+\sqrt{5}}{2} \right ) }^k \cdot \left ( \frac{3+\sqrt{5}}{2} \right ) }-{ { \left ( \frac{1-\sqrt{5}}{2} \right ) }^k \cdot \left ( \frac{3-\sqrt{5}}{2} \right ) } }{\sqrt{5}} \qquad\qquad\qquad\qquad\qquad\,\,\,\, $
onde se observa que para a igualdade ser verdadeira, temos que:
$ \displaystyle \frac{ 3 \pm \sqrt{5} }{2} = { \left ( \frac{ 1\pm \sqrt{5} }{2} \right ) }^2 \, $
$ \displaystyle \frac{ 3 \pm \sqrt{5} }{2} = \frac{ 1\pm 2\sqrt{5}+5 }{4} $
$ \displaystyle \frac{ 3 \pm \sqrt{5} }{2} = \frac{ 6\pm 2\sqrt{5}}{4} \quad\,\,\,\, $
$ \displaystyle \frac{ 3 \pm \sqrt{5} }{2} = \frac{ 3\pm \sqrt{5}}{2} \qquad\, $
Portanto, a igualdade é verdadeira. Logo está provado, por indução, que a equação é verdadeira para todo $n \in \mathbb{Z_+^*} $.
Fibonacci em Outras Mídias
Referências
- HAZZAN, Samuel. Fundamentos de Matemática Elementar. Combinatória. Probabilidade. Vol. 5. São Paulo: Atual, 1997.
- BRASSARD, Gilles; BRATLEY, Paul. Fundamentals of algorithmics. Englewood Cliffs: Prentice Hall, c1996. xx, 524 p. ISBN: 0133350681.
Livraria
