
Considerando um meio homogêneo, infinito em todas as direções, caracterizado por resistividade $ \rho $, conforme representado esquematicamente na figura abaixo

Consideremos uma fonte pontual de corrente $ I $, num ponto $ Q $, em regime estacionário ou variação muito lenta, tem-se
$ \displaystyle J = \sigma \cdot E $
$ \displaystyle E = \rho \cdot J $
Sendo $ E $ o campo elétrico e $ J $ o vetor densidade de corrente de condução.
Em um ponto genérico $ X $, os vetores $ \vec{E} $ e $ \vec{J} $ estão na mesma direção, $ QX $, sendo $ r $ a distância entre $ Q $ e $ X $.
O vetor densidade de corrente é dado por
$ \displaystyle \vec{J} = \frac{I}{ 4 \pi r^{2} } \cdot \frac{ \vec{r} }{r} $
sendo $ 4 \pi r^{2} $ a área de uma esfera, e o vetor campo elétrico por
$ \displaystyle \vec{E} = \frac{ \rho \cdot I }{ 4 \pi r^{2} } \cdot \frac{ \vec{r} }{r} $
O campo elétrico $ E $ está relacionado com um potencial escalar $ V $, tal que, em regime estacionário ou variações muitas lentas,
$ \displaystyle E = – \nabla \cdot V = – \frac{\partial V}{\partial r} $
sendo
$ \displaystyle V = – \int E \cdot dr = – \frac{ \rho \cdot I }{ 4 \pi } \cdot \int \frac{dr}{r^{2}} = \frac{ \rho \cdot I }{ 4 \pi } \cdot \frac{1}{r} + K $
Sendo $ K = 0 $ assumindo que $ V $ tende para zero em pontos infinitamente afastados.
A resistência mútua entre os pontos $ Q $ e $ X $, em reação a um ponto infinitamente afastado, é a relação entre $ V(x) $ e $ I $, para $ K = 0 $, ou
$ \displaystyle R_{XQ} = \frac{ \rho }{ 4 \pi } \cdot \frac{1}{r} = \frac{V}{I} $
Sendo $ r $ a distancia entre os pontos $ Q $ e $ X $.
Campo de Vetores E e J, e Potencial V para uma Fonte de Corrente em Diferentes Meios
Raciocínio similar pode ser aplicado para a obtenção do campo $ E $ e $ J $, e potencial $ V $, associado a uma fonte pontual num meio delimitado por vários planos.
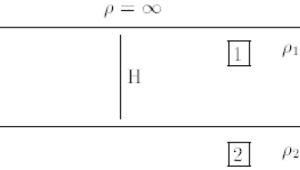
Para uma Fonte Pontual num Solo a duas Camadas

O raciocínio anterior é generalizado a uma fonte pontual de corrente, num meio constituído por regiões homogêneas separadas por planos paralelos, considerando que, em cada plano, uma onda incidente dá origem a uma onda refletida e uma onda transmitida, de acordo com a relação das resistividades das duas regiões separadas pelo plano.
Consideremos, por exemplo, o caso de um solo a três camadas $ 1 $, $ 2 $ e $ 3 $ de resistividades $ \rho_{1} $, $ \rho_{2} $ e $ \rho_{3} $, e uma fonte pontual no meio $ \rho_{1} $, em $ Q $, conforme representado esquematicamente na figura abaixo (sendo $ h < H_{1} $ ).

Considerando a simetria de condição fronteira na superfície do solo, esta condição, abaixo do nível do solo, é equivalente à da figura abaixo.
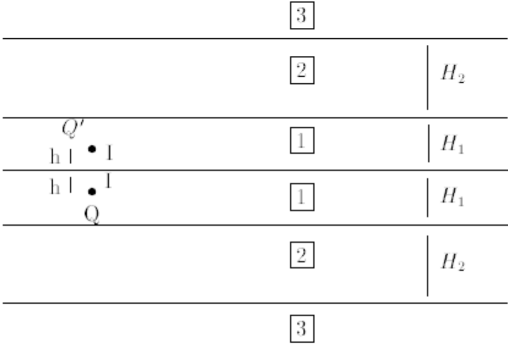
Sejam
$ \displaystyle k_{12} = \frac{ \rho_2-\rho_1 }{ \rho_2+\rho_1 } $
$ \displaystyle k_{12}^{‘} = 1-k_{12} = \frac{ 2 \cdot \rho_1 }{ \rho_2+\rho_1 } $

Referências
- TELLÓ, Marcos (Org), Aterramento elétrico impulsivo, em baixa e alta frequências: com apresentação de casos. Porto Alegre: EdiPUCRS, 2007. 328 p. ISBN: 9788574306230.
- ZANETTA JÚNIOR, Luiz Cera, Transitórios eletromagnéticos em sistemas de potência. São Paulo: EDUSP, 2003. 712 p. (Acadêmica, n.52) ISBN: 8531407559.

