Considerando um meio infinito em todas as direções, caracterizado por resistividades $ \rho_{1} $ e $ \rho_{2} $ em dois domínios $ 1 $ e $ 2 $ separados por um plano P, conforme representado esquematicamente na figura.

Consideremos uma fonte pontual de corrente $ I $, num ponto $ Q $ da região de resistividade $ \rho_{1} $, em regime estacionário ou variação muito lenta, tem-se
$ \displaystyle J = \sigma \cdot E $
$ \displaystyle E = \rho \cdot J $
Na superfície de descontinuidade da região de resistividade $ (P) $ a componente de $ E $ tangencial a $ P $ deve ser contínua e a componente $ J $ normal a $ P $ deve ser contínua (supondo que $ Q $ não está no plano $ P $).
Estas condições podem ser consideradas equivalentes a ondas dos campos $ E $ e $ J $, estacionárias, irradiando de $ Q $ de forma simétrica, que teriam atenuação com o quadrado da distância (para fonte pontual) e se refletem na superfície $ P $. Estas ondas, em $ P $, podem ser consideradas a sobreposição de ondas planas pequenas.
Uma onda plana de vetores $ E $ e $ J $ satisfazendo às condições anteriores é compatibilizada, no plano $ P $, pela sobreposição de três ondas planas, que passamos a designar por incidente, refletida e transmitida, conforme representado esquematicamente na figura.
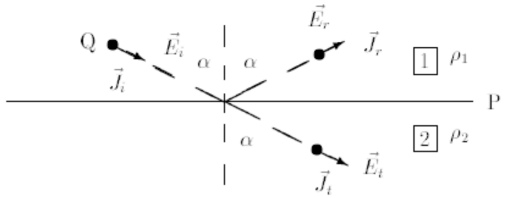
Na superfície $ P $ deve ter-se continuidade da componente $ J $] normal à superfície e continuidade da componente $ E $ tangencial à superfície, o que implica
$ \displaystyle J_{i} \cdot \cos \alpha-J_{r} \cdot \cos \alpha = J_{t} \cdot \cos \alpha $
$ \displaystyle E_{i} \cdot \sin \alpha-E_{r} \cdot \sin \alpha = E_{t} \cdot \sin \alpha $
ou
$ \displaystyle J_{i}-J_{r} = J_{t} $
$ \displaystyle E_{i}-E_{r} = E_{t} $
Tem-se, por outro lado
$ \displaystyle E_{i} = \rho_{1} \cdot J_{i} $
$ \displaystyle E_{r} = \rho_{1} \cdot J_{r} $
$ \displaystyle E_{t} = \rho_{2} \cdot J_{t} $
Donde
$ \displaystyle J_{i}-J_{r} = J_{t} $
$ \displaystyle J_{i}+J_{r} = \frac{\rho_{2}}{\rho_{1}} \cdot J_{t} $
Donde
$ \displaystyle 2 \cdot J_{i} = \left( 1+\frac{\rho_{2}}{\rho_{1}} \right) \cdot J_{t} $
$ \displaystyle J_{t} = \frac{2 \cdot \rho_{1}}{\rho_{2}+\rho_{1}} \cdot J_{i} $
$ \displaystyle J_{r} = J_{i}-J_{t} = \frac{\rho_{2}-\rho_{1}}{\rho_{2}+\rho_{1}} \cdot J_{i} $
logo, para a reflexão, temos
$ \displaystyle J_{r} = k \cdot J_{i} $
$ \displaystyle E_{r} = k \cdot E_{i} $
e para a transmissão
$ \displaystyle J_{t} = \left( 1-k \right) \cdot J_{i} = k^{‘} \cdot J_{i} $
$ \displaystyle E_{t} = \left( 1-k \right) \cdot \frac{\rho_{2}}{\rho_{1}} \cdot E_{i} = k^{”} \cdot E_{i} $
Sendo
$ \displaystyle k = \frac{\rho_{2}-\rho_{1}}{\rho_{2}+\rho_{1}} $
o fator de reflexão, igual à relação entre as amplitudes de $ E $ (ou $ J $) da onda refletida e da incidente, na superfície $ P $, e
$ \displaystyle k^{‘} = 1-k = \frac{2 \cdot \rho_{1}}{\rho_{2}+\rho_{1}} $
o fator de transmissão de $ J $, igual à relação entre as amplitudes de $ J $ da onda transmitida de $ J $ e da onda incidente de $ J $, e
$ \displaystyle k^{”} = \left( 1-k \right) \cdot \frac{\rho_{2}}{\rho_{1}} = \frac{2 \cdot \rho_{2}}{\rho_{2}+\rho_{1}} $
o fator de transmissão de $ E $, igual à relação entre as amplitudes de $ E $ e da onda transmitida de $ E $ e da onda incidente de $ E $.
Por sobreposição de pequenas ondas quase planas, que constituem as ondas esféricas centradas em $ Q $, tem-se que as equações do campo são satisfeitas se considerar, em vez do sistema físico em causa, sistemas físicos equivalentes, que se obtêm por sobreposição de ondas planas de pequeno ângulo divergentes de $ Q $, conforme representado na figura.
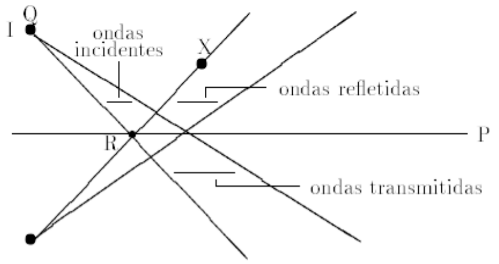
Mais concretamente, o campo no meio $ 1 $, de resistividade $ \rho_{1} $, pode considerar-se a sobreposição do campo criado num meio uniforme, de resistividade $ \rho_{1} $, por uma fonte pontual de corrente $ I $, localizada em $ Q $, e uma fonte pontual de corrente $ I \cdot k $, localizada na imagem, $ Q^{‘} $, de $ Q $ em relação a $ P $, conforme representado esquematicamente na figura.

Num ponto genérico $ X $, o campo criado pela fonte $ I $ em $ Q $ é na direção $ QX $ definido por
$ \displaystyle J_{1} = \frac{I}{4 \pi r^{2}} $
$ \displaystyle E_{1} = \frac{\rho_ {1} \cdot I}{4 \pi r^{2}} $
e o campo criado pela fonte $ I \cdot k $ em $ Q^{‘} $ é na direção $ Q^{‘}X $ e definido por
$ \displaystyle J_{2} = \frac{I \cdot k}{4 \pi {r^{‘}}^{2}} $
$\displaystyle E_{2} = \frac{\rho_ {2} \cdot I \cdot k}{4 \pi {r^{‘}}^{2}} $
O campo $ E_{1} $ está associado a uma função potencial, $ V_{1} $, sendo
$ \displaystyle E_{1} = -\nabla \cdot V_{1} $
$ \displaystyle V_{1}= \frac{\rho_ {1} \cdot I }{4 \pi r}+K_{1} $
Sendo $ K_{1} $ uma constante, que é nula se admitir $ V_{1} = 0 $ em pontos infinitamente afastados.
O campo $ E_{2} $ está associado a uma função potencial, $ V_{2} $, sendo
$ \displaystyle E_{2} = -\nabla \cdot V_{2} $
$ \displaystyle V_{2}= \frac{\rho_ {1} \cdot I \cdot k}{4 \pi r}+K_{2} $
Sendo $ K_{2} $ uma constante, que é nula se admitir $ V_{2} = 0 $ em pontos infinitamente afastados.
O campo resultante, $ \vec{E} $, é tal que
$ \displaystyle \vec{E} = \vec{E}_{1} + \vec{E}_{2} $
$ \displaystyle E = -\nabla \cdot V $
$ \displaystyle V = V_{1}+V_{2} = \frac{\rho_{1} \cdot I}{4 \pi} \left( \frac{1}{r} + \frac{1}{r^{‘}} \right) $
No meio de resistividade $ \rho_{2} $, o campo $ E $ e $ J $, é equivalente à sobreposição de ondas incidentes irradiando de $ Q $, atenuando-se com $ 1/r^{2} $ a partir de $ Q $, e criadas por uma fonte pontual de corrente $ I \cdot k^{‘} = I \cdot \left( 1-k \right) $, conforme representado esquematicamente na figura.
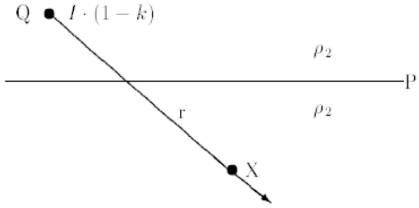
Num ponto genérico $ X $, o campo criado pela fonte $ I \cdot \left( 1-k \right) $ é na direção $ QX $ e definido por
$ \displaystyle J = \frac{I \cdot \left( 1-k \right) }{4 \pi r^{2}} $
$ \displaystyle E = \frac{\rho_ {2} \cdot I \cdot \left( 1-k \right) }{4 \pi r^{2}} $
O campo $ E $ está associado a uma função potencial, $ V $, sendo
$ E = -\nabla \cdot V $
$ \displaystyle V= \frac{\rho_ {2} \cdot I \cdot \left( 1-k \right) }{4 \pi r}+K $
Referências
- TELLÓ, Marcos (Org). Aterramento elétrico impulsivo, em baixa e alta frequências: com apresentação de casos. Porto Alegre: EdiPUCRS, 2007. 328 p. ISBN: 9788574306230.
- ZANETTA JÚNIOR, Luiz Cera. Transitórios eletromagnéticos em sistemas de potência. São Paulo: EDUSP, 2003. 712 p. (Acadêmica, n.52) ISBN: 8531407559.
