Suponhamos o caso de uma fonte pontual, a uma profundidade $ h $, num solo a duas camadas, a superior de profundidade $ H $, conforme representado esquematicamente na figura.
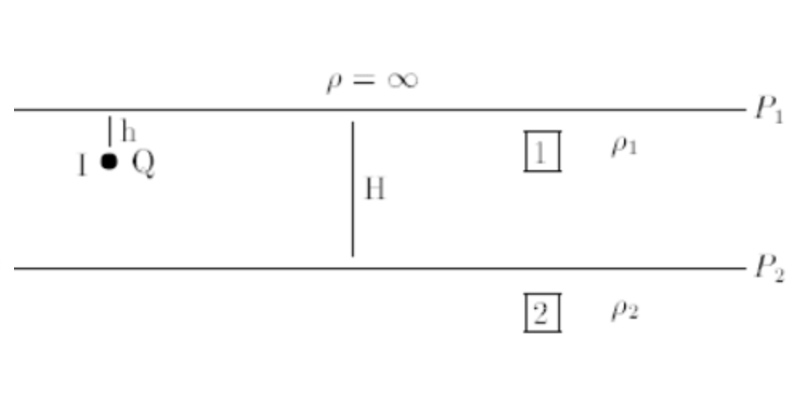
Este campo, como resulta imediatamente da condição de reflexão perfeita $ \left( k=1 \right) $ no solo, e nos meios $ 1 $ e $ 2 $, equivalente ao criado por duas fontes pontuais, nas condições da figura.
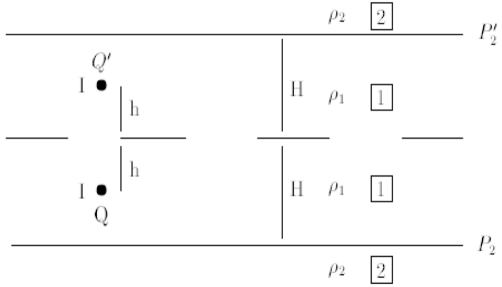
Considerando sucessivas reflexões nos planos $ P_{2} $ e $ P_2^{‘} $ das ondas irradiando de $ Q $ e de $ Q^{‘} $, tem-se que, para efeitos do meio $ 1 $, o potencial $ V $, e os campos $ E $ e $ J $, são idênticos aos criados por uma série de fontes pontuais, num meio uniforme de resistividade $ \rho_{1} $, conforme indicado esquematicamente nas figuras.

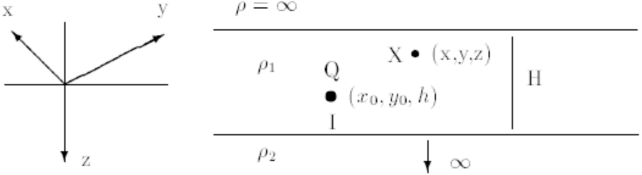
Isto é, o campo no meio $ 1 $ é equivalente ao criado por uma sucessão de fontes de correntes, simétricas em relação ao solo, na vertical de $ Q $, a distância do solo (em sentido algébrico, contadas positivamente a partir do solo, para baixo)
$ \displaystyle \pm h $ ; $ \pm \left( 2H-h \right) $ ; $ \pm \left( 2H+h \right) $ ; $ \pm \left( 4H-h \right) $ ; $ \pm \left( 4H+h \right) $ ; $ \cdots $ $ \pm \left( 2nH-h \right) $ ; $ \pm \left( 2nH+h \right) $ ; $ \cdots $
e com correntes, nessas fontes, da forma $ I \cdot k^{n} $.
O potencial $ V $, num ponto genérico, $ X $, de coordenadas $ x $, $ y $ e $ z $ do meio $ 1 $, associado, à fonte em causa, no ponto $ Q $ de coordenadas $ x_{0} $, $ y_{0} $, $ h $, é
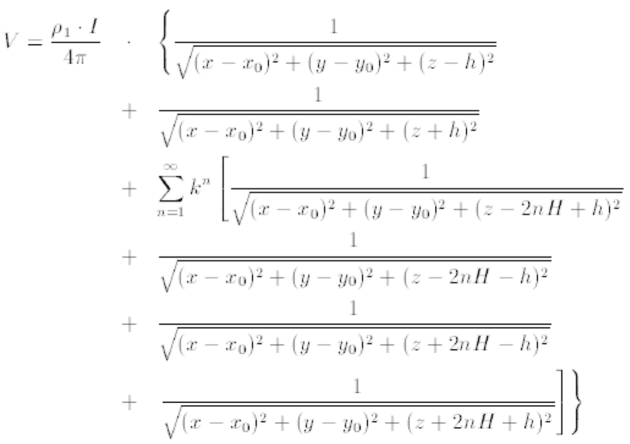
O campo $ E $ e o campo $ J $, num ponto genérico $ X $ do meio $ 1 $, podem ser obtidos a partir de
$ \displaystyle E = -\nabla \cdot V $
$ \displaystyle J = \frac{1}{\rho_{1}} \cdot E $
O campo no meio $ 2 $ é equivalente ao campo criado num meio uniforme de resistividade $ \rho_{2} $, por uma sucessão de fontes pontuais de corrente, na vertical de $ Q $, a distância da superfície do solo (em sentido algébrico)
$ \displaystyle \pm h $ ; $ -\left( 2H-h \right) $ ; $ -\left( 2H+h \right) $ ; $ -\left( 4H-h \right) $ ; $ -\left( 4H+h \right) $ ; $ \cdots $ $ -\left( 2nH-h \right) $ ; $ -\left( 2nH+h \right) $ ; $ \cdots $
e com correntes, nessas fontes, da forma $ I \cdot \left( 1-k^{n} \right) $ conforme representado esquematicamente na figura.

onde
$ \displaystyle E = – \nabla \cdot V $
$ \displaystyle J = \frac{1}{\rho_{2}} \cdot E $
O potencial $ V $, num ponto genérico, $ X $, de coordenadas $ x $, $ y $ e $ z $ do meio $ 2 $, associado, à fonte em causa, no ponto $ Q $ de coordenadas $ x_{0} $, $ y_{0} $, $ h $, é

Acima do solo tem-se $ J = 0 $ e o campo elétrico é idêntico ao que se teria num meio homogêneo de resistividade $ \rho_{1} $ associado a uma sucessão de fontes pontuais de corrente, na vertical de $ Q $, a distância do solo, em sentido algébrico,
$ h $ ; $ 2H-h $ ; $ 2H+h $ ; $ 4H-h $ ; $ 4H+h $ ; $ 6H-h $ ; $ 6H+h $ ; $ \cdots $ $ 2nH-h $ ; $ 2nH+h $ ; $ \cdots $
e com correntes, nessas fontes, da forma $ I \cdot 2 \cdot k^{n} $ conforme representado na figura.
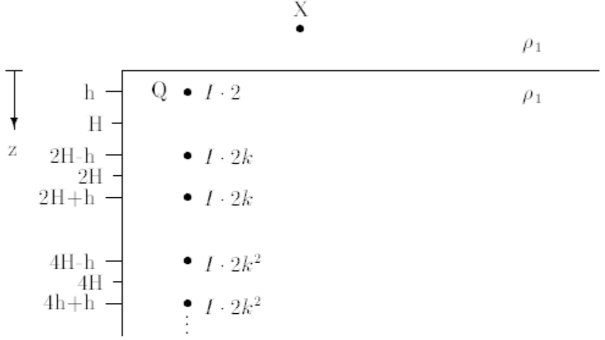
O campo potencial, $ V $, num ponto genérico $ X $ acima do solo, de coordenadas $ x $, $ y $ e $ z $, com $ z \leqslant 0 $, é
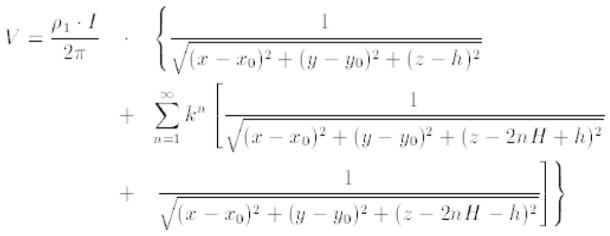
e
$ \displaystyle E = -\nabla \cdot V $
$ \displaystyle J = 0 $
Obviamente, se se dividir $ V $ por $ I $ nas expressões de $ V \left( x \right) $, tem-se a resistência mútua entre o ponto $ Q $ e o ponto $ X $:
$ \displaystyle R_{QX} = \frac{V \left( x \right) }{I} $
Sendo $ R_{QX} $ a relação entre o potencial no ponto $ X $ e a corrente $ I $ injetada no ponto $ Q $ (com a condição de o potencial tender para zero em pontos infinitamente afastados de $ Q $).
Consideremos agora uma fonte pontual de corrente no meio $ 2 $, num ponto $ Q $ de coordenadas $ x_{0} $, $ y_{0} $ e $ h $, conforme representado esquematicamente na figura.

O que é equivalente, no solo, ao campo criado pelas duas fontes pontuais nas condições da figura.

Para efeitos dos campos $ E $ e $ J $, e do potencial $ V $, no meio $ 2 $, as condições da figura acima so equivalentes às da figura abaixo, correspondente a, num meio homogêneo da resistividade $ \rho_{2} $, uma sucessão de fontes de corrente na vertical do ponto $ Q $, de coordenadas $ z $

$ h $ ; $ 2H-h $ ; $ -h $ ; $ -\left( 2H+h \right) $ ; $ -\left( 4H+h \right) $ ; $ \cdots $ ; $ -\left( 2nH-h \right) $ ; $ \cdots $
Para $ n = 0 $; $ 1 $, $ 2 $; $ \cdots $, sendo as correntes destas fontes pontais, respectivamente,

O potencial $ V $ criado por estas fontes de corrente num ponto genérico $ X $ do meio $ 2 $, de coordenadas $ x $, $ y $ e $ z $, é

O campo $ E $, no meio $ 2 $, é
$ \displaystyle E = -\nabla \cdot V $
$ \displaystyle J = \frac{1}{\rho_{2}} \cdot E $
A resistência entre os pontos $ Q $ e $ X $ é
$ \displaystyle R_{QX} = \frac{V}{I} $
A resistência mútua entre o ponto $ Q $ e um ponto genérico do meio $ 1 $ pode ser calculada de maneira similar. Pode demonstrar-se, todavia, que a resistência mútua $ R_{QX} $, sendo $ Q $ um ponto do meio $ 2 $, onde se considera a fonte pontual de corrente, e $ X $ um ponto do meio $ 1 $, é igual à resistência mútua $ R_{QX} $ associada a uma fonte pontual de corrente no meio $ 1 $, no ponto $ X $.
Referências
- TELLÓ, Marcos (Org). Aterramento elétrico impulsivo, em baixa e alta frequências: com apresentação de casos. Porto Alegre: EdiPUCRS, 2007. 328 p. ISBN: 9788574306230.
- ZANETTA JÚNIOR, Luiz Cera. Transitórios eletromagnéticos em sistemas de potência. São Paulo: EDUSP, 2003. 712 p. (Acadêmica, n.52) ISBN: 8531407559.
