Transformação $ \alpha\beta $
Considere as duas estruturas trifásica e bifásica, figura abaixo.
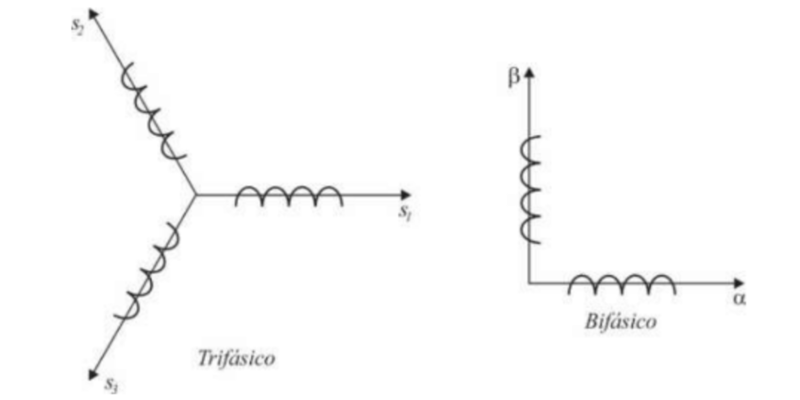
É possível converter uma estrutura trifásica a uma estrutura bifásica equivalente a partir da transformação:
$ \displaystyle \begin{bmatrix}
{x_\alpha} \\
{x_\beta} \\
\end{bmatrix}
= \begin{bmatrix}
1 & {-\frac{1}{2}} & {-\frac{1}{2}} \\
0 & {\frac{\sqrt{3}}{2}} & {-\frac{\sqrt{3}}{2}}
\end{bmatrix}
\begin{bmatrix}
{x_1} \\
{x_2} \\
{x_3}
\end{bmatrix} $
A matriz transformação é formada por termos constantes. Portanto as variáveis $ \alpha \beta $ possuem a mesma natureza das $ 123 $.
Admitindo-se que os sistemas trifásicos e bifásicos são compostos de enrolamentos com $ N_3 $ e $ N_2 $ espiras, figura abaixo.
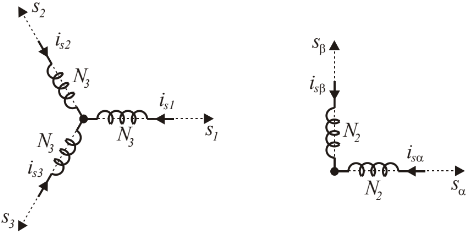
$ \displaystyle \begin{bmatrix}
{x_\alpha} \\
{x_\beta} \\
\end{bmatrix}
=
\frac{N_3}{N_2} \begin{bmatrix}
1 & {-\frac{1}{2}} & {-\frac{1}{2}} \\
0 & {\frac{\sqrt{3}}{2}} & {-\frac{\sqrt{3}}{2}}
\end{bmatrix}
\begin{bmatrix}
{x_1} \\
{x_2} \\
{x_3}
\end{bmatrix} $
A matrix de transformação permite a transformação $ 123 \rightarrow \alpha\beta $. Porém, como ela não tem inversa, a transformação $ \alpha\beta \rightarrow 123 $ não é possível.
Para que se possa inverter a matriz é necessário acrescentar uma linha para que sua dimensão se torne 3×3. Para tal, é inserido um eixo a mais na transformação que não tem conexão com os demais, denominado de homopolar.
$ \displaystyle \begin{bmatrix}
{x_0} \\
{x_\alpha} \\
{x_\beta} \\
\end{bmatrix}
=
\frac{N_3}{N_2} \begin{bmatrix}
a & a & a \\
1 & {-\frac{1}{2}} & {-\frac{1}{2}} \\
0 & {\frac{\sqrt{3}}{2}} & {-\frac{\sqrt{3}}{2}}
\end{bmatrix}
\begin{bmatrix}
{x_1} \\
{x_2} \\
{x_3}
\end{bmatrix} $
A componente homopolar é composta pela contribuição proporcional das três fases e só é representativa quando há assimetrias.
Os valores de $ N_3 $ / $ N_2 $ e $ a $, podem ser definidos de forma que a matriz inversa seja igual a transposta. Assim, a matriz resultante passa a ser:
$ \displaystyle \begin{bmatrix}
x_0 \\
x_\alpha \\
x_\beta \\
\end{bmatrix}
=
\sqrt{\frac{2}{3}} \begin{bmatrix}
{\frac{1}{\sqrt{2}}} & {\frac{1}{\sqrt{2}}} & {\frac{1}{\sqrt{2}}} \\
1 & {-\frac{1}{2}} & {-\frac{1}{2}} \\
0 & {\frac{\sqrt{3}}{2}} & {-\frac{\sqrt{3}}{2}}
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
x_3
\end{bmatrix} $
As variáveis $ 123 $ podem ser: tensões, correntes ou fluxos.
Se as variáveis de entrada $ 123 $ forem senoidais, defasadas entre si de $ 120^\circ $ e simétricas, as variáveis $ \alpha\beta $ será também senoidais, de mesma amplitude e defasadas entre si de $ 90^\circ $.
As variáveis $ \alpha\beta $ podem ser expressas em função de senos e cossenos.
A matriz inversa da transformação $ 123 \rightarrow 0\alpha\beta $ corresponde a sua transposta, ou seja:
$ \displaystyle \begin{bmatrix}
x_1 \\
x_2 \\
x_3
\end{bmatrix}
=
\sqrt{\frac{2}{3}} \begin{bmatrix}
{\frac{1}{\sqrt{2}}} & 1 & 0 \\
{\frac{1}{\sqrt{2}}} & {-\frac{1}{2}} & {\frac{\sqrt{3}}{2}} \\
{\frac{1}{\sqrt{2}}} & {-\frac{1}{2}} & {-\frac{\sqrt{3}}{2}}
\end{bmatrix}
\begin{bmatrix}
x_0 \\
x_\alpha \\
x_\beta
\end{bmatrix} $
Considerando-se que as tensões dadas por:
$ \displaystyle \begin{cases}
v_1(t) = V \cos(\omega_st) \\
v_2(t) = V \cos(\omega_st-120^\circ) \\
v_3(t) = V \cos(\omega_st+120^\circ)
\end{cases}$
As tensões resultantes no sistema bifásico $ \alpha\beta $ são dadas por:
$ \displaystyle \begin{cases}
v_{\alpha}(t) = V^{‘} \cos(\omega_st) \\
v_{\beta}(t) = V^{‘} \sin(\omega_st)
\end{cases}$
As variáveis obtidas são desacopladas entre si. Ou seja, a variável $ \alpha $ não tem influência sobre a variável $ \beta $ e vice-versa.
O seu uso no modelo de máquinas elétricas promove o desacoplamento entre variáveis e eliminam as indutâncias mútuas do mesmo enrolamento.
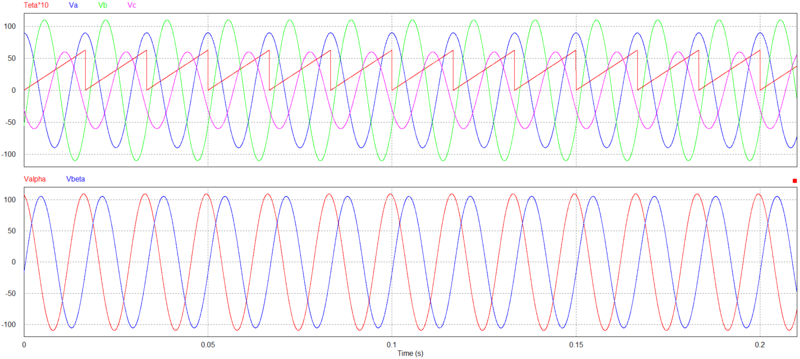
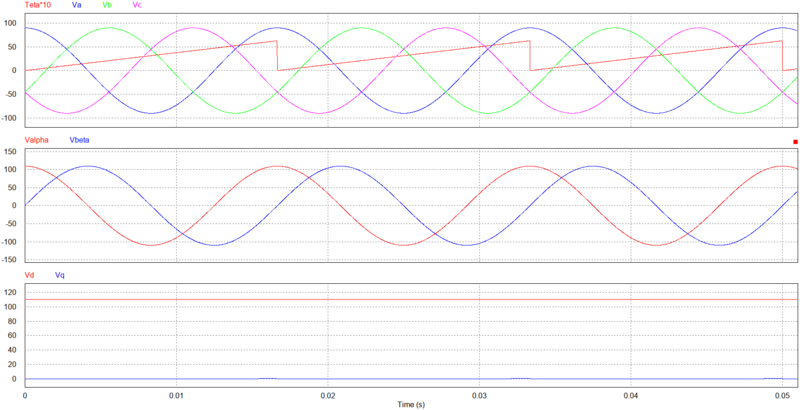
Considere a simulação em que tensões trifásicas $ 123 $ são transformadas em tensões bifásicas $ \alpha\beta $. $ V_{LL} = 110 $V (RMS)
$ \displaystyle \begin{cases}
v_a(t) = 89.81 \cos(\omega_st) \\
v_b(t) = 89.81 \cos(\omega_st-120^\circ) \\
v_c(t) = 89.81 \cos(\omega_st+120^\circ)
\end{cases}$

Considere o seguinte sistema desbalanceado:
$ \displaystyle \begin{cases}
v_a(t) = 89.81 \cos(\omega_st) \\
v_b(t) = 110 \cos(\omega_st-120^\circ) \\
v_c(t) = 60 \cos(\omega_st+120^\circ)
\end{cases}$
Transformação $ 0dq $
Como $ \alpha\beta $ são ortogonais entre si, é possível fazer uma analogia com variáveis complexas.

A partir das variáveis $ \alpha\beta $ definidas por:
$ \displaystyle \begin{cases}
v_{\alpha}(t) = V^{‘} \cos(\omega_st) \\
v_{\beta}(t) = V^{‘} \sin(\omega_st)
\end{cases}$
É possível definir um vetor tensão dado por:
$ \vec{V}=V_\alpha+jV_\beta $
Para um sistema equilibrado, o vetor tensão tem magnitude constante e gira no sentido anti-horário com velocidade $ \omega_s $.
A trajetória do vetor tensão corresponde a um círculo cujo o raio é a sua magnitude.
A transformação $ 123 \rightarrow 0dq $ permite também a obtenção de um sistema bifásico equivalente a partir do sistema trifásico original.

A transformação $ 123 \rightarrow 0dq $ pode ser obtida a partir de:
$ \displaystyle \begin{bmatrix}
{x_0} \\
{x_d} \\
{x_q} \\
\end{bmatrix}
=
\sqrt{\frac{2}{3}} \begin{bmatrix}
1/\sqrt{2} & 1/\sqrt{2} & 1/\sqrt{2} \\
\cos(\theta) & \cos(\theta-2\pi/3) & \cos(\theta-4\pi/3) \\
-\sin(\theta) & -\sin(\theta-2\pi/3) & -\sin(\theta-4\pi/3)
\end{bmatrix}
\begin{bmatrix}
{x_1} \\
{x_2} \\
{x_3}
\end{bmatrix}$
As grandezas em dq podem ser constantes ou possuir frequência diferente do sistema trifásico original.
Elas são defasadas entre si de $ 90^\circ $ e o sistema obtido pode girar segundo o seu alinhamento com o eixo rotacional escolhido.
O seu uso no modelo de máquinas elétricas promove o desacoplamento entre variáveis e eliminam as indutâncias mútuas do mesmo enrolamento.
A transformação $ 0dq \rightarrow 123 $ pode ser obtida a partir de:
$ \displaystyle \begin{bmatrix}
{x_1} \\
{x_2} \\
{x_3} \\
\end{bmatrix}
=
\sqrt{\frac{2}{3}} \begin{bmatrix}
1/\sqrt{2} & \cos(\theta) & -\sin(\theta) \\
1/\sqrt{2} & \cos(\theta-2\pi/3) & -\sin(\theta-2\pi/3) \\
1/\sqrt{2} & \cos(\theta-4\pi/3) & -\sin(\theta-4\pi/3)
\end{bmatrix}
\begin{bmatrix}
{x_0} \\
{x_d} \\
{x_q}
\end{bmatrix} $
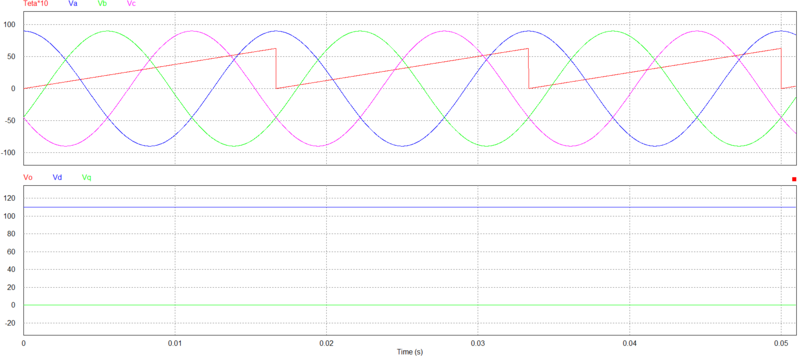
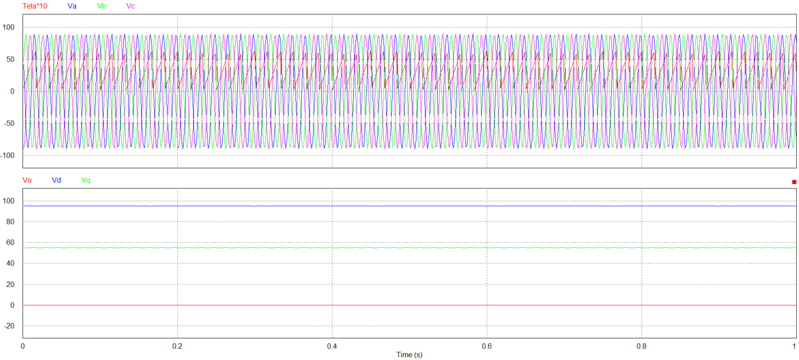
Considere a simulação em que tensões trifásicas $ 123 $ são transformadas em tensões bifásicas $ 0dq $. $ V_{LL} = 110 $V (RMS)
$ \displaystyle \begin{cases}
v_a(t) = 89.81 \cos(\omega_st) \\
v_b(t) = 89.81 \cos(\omega_st-120^\circ) \\
v_c(t) = 89.81 \cos(\omega_st+120^\circ)
\end{cases} $
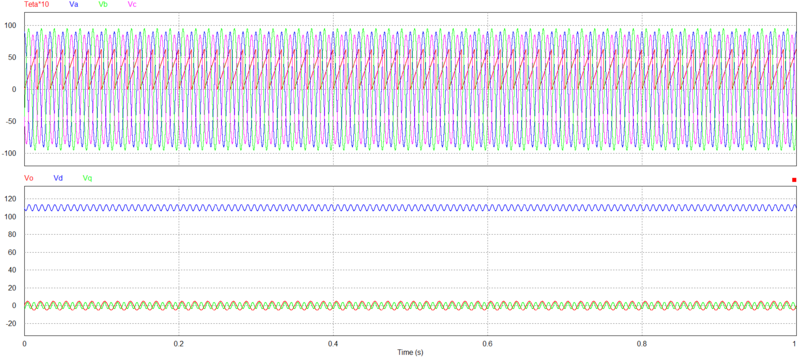
Considere o seguinte sistema com erro de estimação de $ -30^\circ $:
$ \displaystyle \begin{cases}
v_a(t) = 89.81 \sin(\omega_st-30^\circ) \\
v_b(t) = 89.81 \sin(\omega_st-150^\circ) \\
v_c(t) = 89.81 \sin(\omega_st+90^\circ)
\end{cases} $
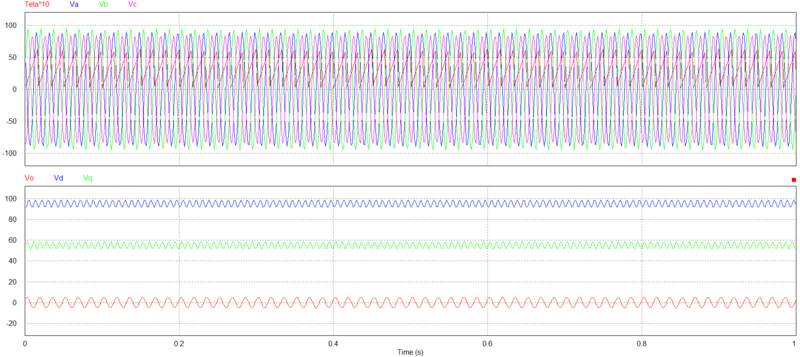
Considere o seguinte sistema desbalanceado:
$ \displaystyle \begin{cases}
v_a(t) = 89.81 \cos(\omega_st) \\
v_b(t) = 95 \cos(\omega_st-120^\circ) \\
v_c(t) = 85 \cos(\omega_st+120^\circ)
\end{cases} $
Considere o seguinte sistema desbalanceado e com erro de estimação de $ -30^\circ $:
$ \displaystyle \begin{cases}
v_a(t) = 89.81 \sin(\omega_st-30^\circ) \\
v_b(t) = 95 \sin(\omega_st-150^\circ) \\
v_c(t) = 85 \sin(\omega_st+90^\circ)
\end{cases} $
Transformação $ \alpha\beta – dq – 0dq $
Na transformação $ \alpha\beta $, o posicionamento do eixo \alpha é alinhado com a fase $ s_1 $ do sistema trifásico e as grandezas obtidas são senoidais.
Outra possibilidade seria o alinhamento do eixo horizontal do sistema bifásico com o vetor tensão, ilustrado na figura abaixo.
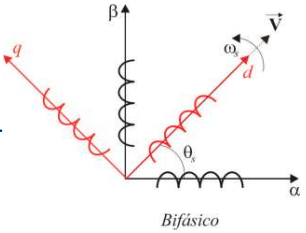
Ou seja, a partir do sistema $ \alpha\beta $ é possível definir um $ dq $ da seguinte forma:
$ \displaystyle \begin{bmatrix}
{x_d} \\
{x_q}
\end{bmatrix}
=
\begin{bmatrix}
\cos \theta_s & \sin \theta_s \\
-\sin \theta_s & \cos \theta_s
\end{bmatrix}
\begin{bmatrix}
{x_\alpha} \\
{x_\beta}
\end{bmatrix} $
A transformação inversa $ dq \rightarrow \alpha\beta $ corresponde a transposta, ou seja:
$ \displaystyle \begin{bmatrix}
{x_\alpha} \\
{x_\beta}
\end{bmatrix}
=
\begin{bmatrix}
\cos \theta_s & -\sin \theta_s \\
\sin \theta_s & \cos \theta_s
\end{bmatrix}
\begin{bmatrix}
{x_d} \\
{x_q}
\end{bmatrix} $
Considerando a simulação em que tensões trifásicas $ 123 $ são transformadas em tensões bifásicas $ \alpha\beta $, temos:
$ \displaystyle \begin{bmatrix}
{v_d} \\
{v_q}
\end{bmatrix}
=
\begin{bmatrix}
\cos \theta_s & \sin \theta_s \\
-\sin \theta_s & \cos \theta_s
\end{bmatrix}
\begin{bmatrix}
{v_\alpha} \\
{x_\beta}
\end{bmatrix}
=
\begin{bmatrix}
{\cos \theta_s V^{‘} \cos \theta_s} & {\sin \theta_s V^{‘} \sin \theta_s} \\
{ -\sin \theta_s V^{‘} \cos \theta_s} & {\cos \theta_s V^{‘} \sin \theta_s}
\end{bmatrix}
=
\begin{bmatrix}
V^{‘} \\
0
\end{bmatrix} $
Para $ V_{LL} = 110 $V (RMS), obtêm-se
$ \displaystyle \begin{cases}
v_a(t) = 89.81 \cos(\omega_st) \\
v_b(t) = 89.81 \cos(\omega_st-120^\circ) \\
v_c(t) = 89.81 \cos(\omega_st+120^\circ)
\end{cases}
\quad
\begin{cases}
v_{\alpha}(t) = 110 \cos(\omega_st) \\
v_{\beta}(t) = 110 \sin(\omega_st)
\end{cases}
\quad
\begin{cases}
v_d = 110 \\
v_d = 0
\end{cases} $
Diretamente a transformação $ 123 \rightarrow 0dq $ sem os procedimentos intermediários pode ser obtida a partir de:
$ \displaystyle \begin{bmatrix}
{x_0} \\
{x_d} \\
{x_q} \\
\end{bmatrix}
=
\sqrt{\frac{2}{3}} \begin{bmatrix}
1/\sqrt{2} & 1/\sqrt{2} & 1/\sqrt{2} \\
\cos(\theta_s) & \cos(\theta_s-2\pi/3) & \cos(\theta_s-4\pi/3) \\
-\sin(\theta_s) & -\sin(\theta_s-2\pi/3) & -\sin(\theta_s-4\pi/3)
\end{bmatrix}
\begin{bmatrix}
{x_1} \\
{x_2} \\
{x_3}
\end{bmatrix} $
com sua inversa dada por:
$ \displaystyle \begin{bmatrix}
{x_1} \\
{x_2} \\
{x_3} \\
\end{bmatrix}
=
\sqrt{\frac{2}{3}} \begin{bmatrix}
1/\sqrt{2} & \cos(\theta_s) & -\sin(\theta_s) \\
1/\sqrt{2} & \cos(\theta_s-2\pi/3) & -\sin(\theta_s-2\pi/3) \\
1/\sqrt{2} & \cos(\theta_s-4\pi/3) & -\sin(\theta_s-4\pi/3)
\end{bmatrix}
\begin{bmatrix}
{x_0} \\
{x_d} \\
{x_q}
\end{bmatrix} $
Potência no Sistema Bifásico $ 0\alpha\beta $
Baseados nas variáveis de tensão e de corrente em $ \alpha\beta $ é possível definir as potências, ativa e reativa.
A potência aparente pode ser dada por:
$ S = VI^* $
Escrevendo a corrente em tensão em termos de variáveis complexas,
$ V = v_\alpha + jv_\beta $
$ I = i_\alpha + ji_\beta $
Desta forma, a potência aparente pode ser calculado como:
$ S = P+jQ = (v_\alpha + jv_\beta)(i_\alpha + ji_\beta) $
Assim a potência ativa pode ser dada por:
$ P = v_\alpha i_\alpha + v_\beta i_\beta $
E a potência reativa:
$ Q = v_\beta i_\alpha – v_\alpha i_\beta $
As potências ativa e reativa são portanto dadas por:
$\begin{cases}
P = v_\alpha i_\alpha + v_\beta i_\beta \\
Q = v_\beta i_\alpha – v_\alpha i_\beta
\end{cases}$
Do ponto de vista analítico, algumas observações são pertinentes:
A transformação $ 0\alpha\beta $ é obtida a partir de uma matriz [T] composta por termos constantes, o que resulta em variáveis $ \alpha\beta $ de mesma natureza das trifásicas $ 123 $ (senoidais).
As grandezas serão também senoidais com termos constantes e senoidais de frequência $ 2 \omega_s t $ (duas vezes a frequência da rede elétrica).
As grandezas senoidais podem ser tratadas para definição de estratégias de controle de fluxo de potência, mas tem complexidade considerável,
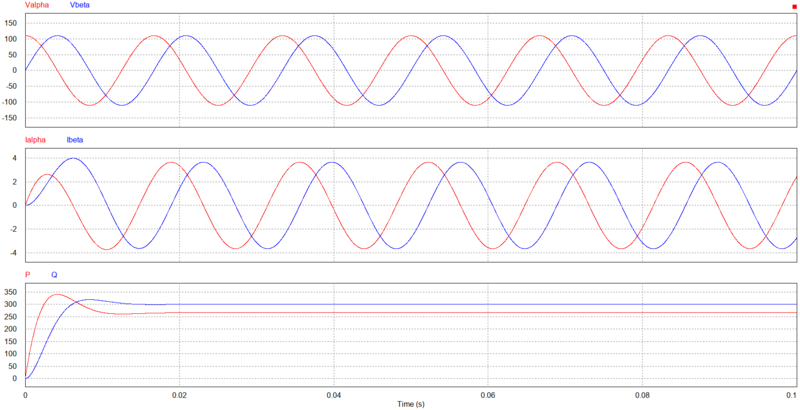
Exemplo: Obter a potência ativa e reativa de uma carga de $ 20 \Omega $ e $ 60mH $ alimentado por uma fonte com tensão de fase $ 63,57 V $ (RMS) a 60Hz.
$ Z = 20 + j(377)(0,06) = 20+j22,62 $ A
$ I = \frac{V}{Z} = 1,39-j1,5755 $ A
$ S = VI^* = 3(63,57)(1,39+j1,5755) = 265,09+j300,46 $ VA
Potência no Sistema Bifásico $ 0dq $
Baseados nas variáveis de tensão e de corrente em $ dq $ é possível definir as potências aparente, ativa e reativa.
A potência aparente pode ser dada por:
$ S = VI^* $
Escrevendo a corrente em tensão em termos de variáveis complexas,
$ V = v_d+jv_q $
$ I = i_d+ji_q $
Desta forma, a potência aparente pode ser calculado como:
$ S = P + jQ = (v_d+jv_q)(i_d-ji_q) $
Assim a potência ativa pode ser dada por:
$ P = v_{d}i_{d}+v_{q}i_{q} $
e a potência reativa:
$ Q = v_{q}i_{d}-v_{d}i_{q} $
Do ponto de vista analítico, algumas observações são pertinentes:
A transformação $ 0dq $ é realizada por uma matriz [T] composta por elementos dependente de $ \theta_s $ (ângulo do vetor tensão) e consequentemente resulta em grandezas constantes.
As grandezas $ dq $ podem ser tratadas para definição de estratégias de controle de fluxo de potência, mas tem complexidades considerável.
Como visto anteriormente, no caso do sistema de alimentação simétrico e equilibrado, a componente do eixo $ q ( v_q = 0 ) $ é nula, ou seja:
$ P = v_di_d $
$ Q = -v_di_q $
A transformação $ 0dq $ permite desacoplar os termos de potência ativa e reativa. Assim, é possível impor a potência ativa regulando-se $ i_d $ e a potência reativa regulando-se $ i_q $.
A conclusão acima permite associar conversores de potência e técnicas de controle para implementação de estratégias de controle de fluxo de potência.
Salienta-se que o tratamento matemático só encontra aplicação prática se o ângulo do vetor tensão $ \theta_s $ for completamente conhecido.
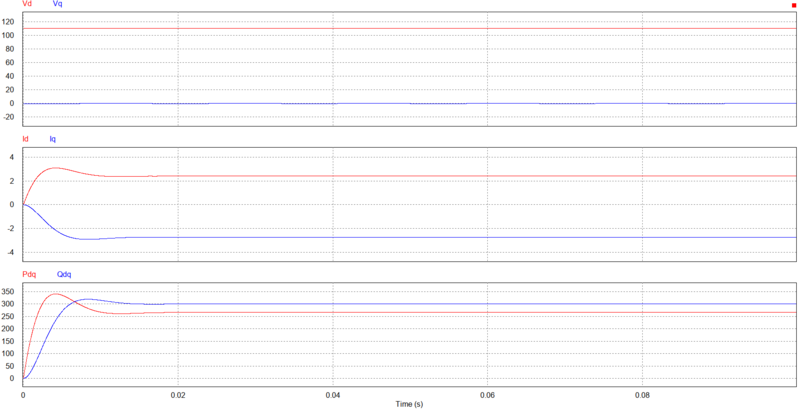
Exemplo: Obter a potência ativa e reativa de uma carga de $ 20 \Omega $ e $ 60mH $ alimentado por uma fonte com tensão de fase $ 63,57 V $ (RMS) a 60Hz.
$ Z = 20 + j(377)(0,06) = 20+j22,62 $ A
$ I = \frac{V}{Z} = 1,39-j1,5755 $ A
$ S = VI^* = 3(63,57)(1,39+j1,5755) = 265,09+j300,46 $ VA
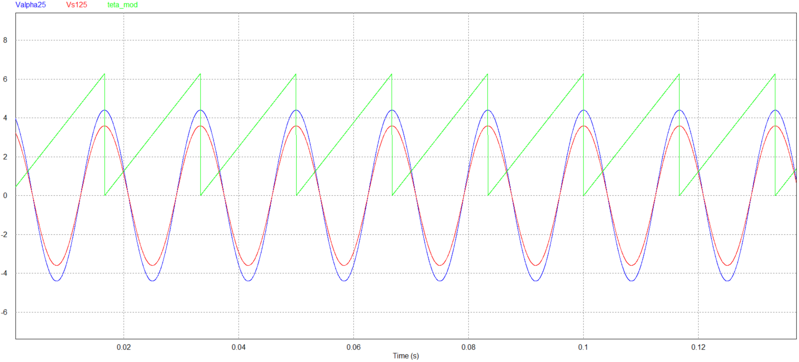
Determinação do $ \theta_s $
O tratamento matemático só encontra aplicação prática se o ângulo do vetor tensão $ \theta_s $ for completamente conhecido.
É possível obter o ângulo do vetor tensão $ \theta_s $ a partir das componentes do sistema bifásico $ \alpha\beta $.
A partir do vetor tensão, as componentes $ \alpha\beta $ podem ser dadas por:
$\begin{cases}
v_\alpha = V\cos \theta_s \\
v_\beta = V\sin \theta_s
\end{cases}$
Em que:
$ V = \sqrt{v_\alpha^2+v_\beta^2} $
Combinando com as definições anteriores, pode-se escrever:
$ \cos \theta_s = \frac{v_\alpha}{\sqrt{v_\alpha^2+v_\beta²}} \quad \sin \theta_s = \frac{v_\beta}{\sqrt{v_\alpha^2+v_\beta²}} \quad \tan \theta_s = \frac{\sin \theta_s}{\cos \theta_s} $

Sincronização com a Rede Elétrica
Destacam-se os esquemas de detecção de passagem por zero da tensão e as técnicas PLL (do inglês, Phase Locked Loop).
Os esquemas de passagem por zero são de simples implementação, mas de pouca eficiência, principalmente quando há distúrbios na forma de onda da tensão.
O princípio de funcionamento do PLL é zerar a diferença entre os ângulos do vetor tensão e do sinal gerado na sua saída.
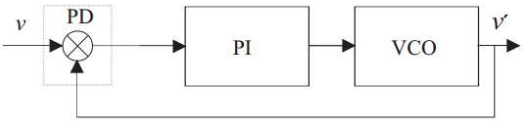
Nesse diagrama, o bloco PD (do inglês, Phase Detector) realiza a detecção da defasagem entre os sinais de entrada v e saída v, do PLL.
Com base nessa defasagem (erro), o PI gera um sinal de controle para o oscilador controlado por tensão VCO (do inglês, Voltage-Controlled-Oscilator), que produz na sua saída um sinal elétrico correspondente ao ângulo do vetor tensão.
Uma alternativa para implementação do PLL é a utilização da detecção de fase baseada na geração de sinais em quadratura.
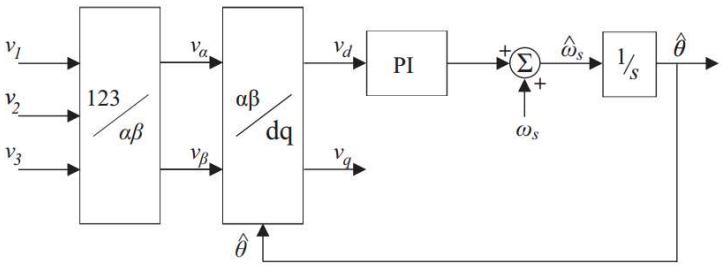
Nesse diagrama de blocos, $ \omega_s $ é a frequência da rede (rad/s) e $ \hat{\omega_s} $ é a frequência instantânea (rad/s).
No caso dos sistemas monofásicos, a transformação do referencial $ 123 $ para $ \alpha\beta $ ou para $ dq $ é realizada utilizando-se a tensão da rede elétrica como a componente $ \alpha $ e a emulação da componente $ \beta $ a partir da defasagem desta em $ 90^\circ $.
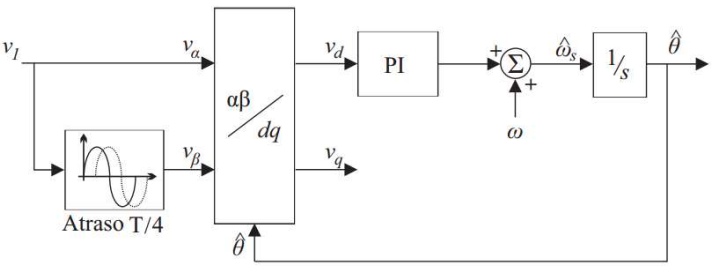
Para isso, utiliza-se um filtro passa baixa com um retardo de $ 1/4 $ do período da fundamental ou um filtro passa tudo.
Synchronous Reference Frame Phase-Locked-Lood. Força-se que o vetor $ v_q $ seja nulo na estimação.

Referências
- Notas de aula do prof. dr. Caio Dorneles Cunha e prof. dr. Thiago de Oliveira Alves Rocha.
- Mohan, Undeland e Robbins, Power Electronics. Willey, 1989.
- W. Leonard, Control of Electrical Drives. Springer, 2001 2Ed.
- M. E. El-Hawary, Modeling and High Performance Control of Electric Machines. John Wiley & Sons, 2005.
- Chen-Mun Ong, Dynamic Simulation of Electric Machinery. Prentice-Hall, 1997.
- R. Krishnan, Eletric Motor Drives, Modeling, Analysis, and Control. Prentice-Hall, 2001.
- Ned Mohan, Máquinas Elétricas e Acionamentos. LTC, 2015.
- Ivo Barbi, Teoria Fundamental do Motor de Indução. Editora da UFSC/ELETROBRÁS, 1985.
