Aqui trataremos das características básicas do funcionamento da máquina CA.
Máquinas CA são construídas de um estator e um rotor que possuem enrolamentos interagindo entre si de tal maneira que se têm dois campos magnéticos girantes. Estas máquinas podem atuar como motores ou geradores de energia, dependendo de sua aplicação.
Os motores CA são classificados geralmente em dois tipos principais: motores síncronos e os motores assíncronos.
Motores Síncronos
O motor síncrono é um alternador funcionando como motor:
No estator dos motores síncronos aplica-se uma tensão alternada nos terminais de suas bobinas que induzem uma corrente alternada (CA) em cada uma delas provocando um campo girante.
No rotor dos motores síncronos aplica-se ao terminal de sua bobina uma tensão contínua por meio de escovas, fazendo com que ele passe a atuar como um ímã permanente.
Motores Assíncronos
O motor assíncrono, aqui chamado de motor de indução difere do motor síncrono por não ter seu rotor ligado a qualquer fonte de alimentação, sendo o seu rotor alimentado por indução magnética. Estas características do motor de indução resultam do fato de ser o rotor uma unidade auto-suficiente que não necessita de conexões externas.
Neste artigo daremos ênfase aos motores assíncronos (ou motores de indução) deixando os motores síncronos para outra oportunidade.
Motor de Indução
O nome “motor de indução” é dado devido ao fato de serem induzidas correntes alternadas no circuito do rotor (ação de transformador), pelo campo magnético girante produzido nas bobinas do estator.
Qual as diferenças do transformador para o motor de indução?! Um motor de indução tem um circuito campo independente. Desta forma seu modelo não contém uma fonte de tensão interna, como no caso da tensão gerada interna $ E_A $ de uma máquina síncrona.
O motor de indução é uma máquina CA que apresenta características bastante apreciadas para acionamentos estáticos a velocidade variável.
Robustez, simplicidade de construção (não tem necessidade de escovas) e baixo custo.
A construção do estator do motor de indução é geralmente semelhante ao do estator do motor síncrono, com uma construção em triângulo delta $ (\Delta) $ ou em estrela $ (Y) $, mas o mesmo não ocorrem em seus rotores. O rotor do motor de indução é um cilindro laminado, com ranhuras na superfície. Os enrolamentos colocados nessas ranhuras podem ser de dois tipos: O tipo rotor de gaiola e rotor bobinado (ou rotor enrolado).
O nome “rotor bobinado” é dado ao fato desta máquina possuir acesso as bobinas do rotor. Já o “gaiola de esquilo” se deve ao fato de os condutores destas máquinas serem semelhantes àquelas rodas nas quais os roedores correm fazendo exercício.
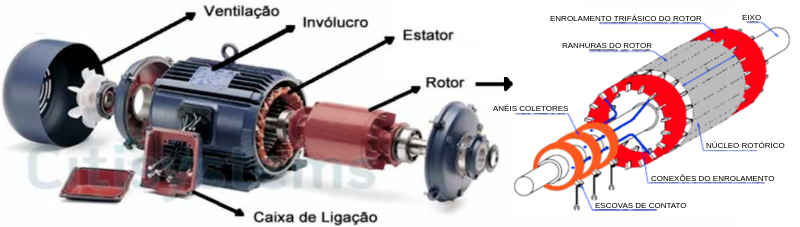
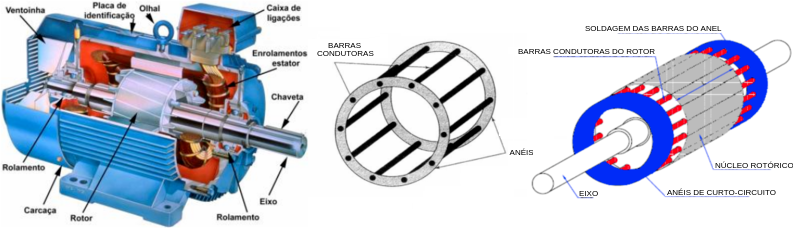
Motores de indução. (a) Rotor bobinado. (b) Gaiola de esquilo.
Rotor bobinado
Um rotor bobinado tem um conjunto completo de enrolamentos trifásicos que são similares aos enrolamentos do estator.
Nos motores de indução de rotor bobinado, as correntes no rotor podem ser acessadas por meio de escovas, nas quais as correntes podem ser examinadas e resistências extras podem ser inseridas no circuito do rotor.
É possível tirar proveito desses atributos para modificar a característica de conjugado versus velocidade do motor.
Um conjunto trifásico de tensões produzem um campo magnético $ B_s $, que está girando em sentido anti-horário. A velocidade de rotação do campo magnético é dada por
$ \displaystyle \eta_{sinc} = \frac{120f_{se}}{P} $
É o movimento relativo do rotor em relação ao campo magnético do estator que produz uma tensão induzida em uma barra do rotor.
Como a estrutura do rotor é indutiva, a corrente de pico do rotor está atrasada em relação à tensão de pico do rotor. O fluxo de corrente do rotor produz um campo magnético de rotor $ B_R $.
Finalmente, como o conjugado induzido na máquina é dado por
$ \displaystyle \tau_{ind} = kB_R \times B_S $
Entretando, há um limite superior finito para a velocidade do motor.
Se o rotor do motor de indução estivesse girando na velocidade síncrona, as barras do rotor estariam estacionárias em relação ao campo magnético $ B_S $ e não haveria tensão induzida.
Se $ e_{ind} $ fosse igual a 0, então não haveria corrente nem campo magnético no rotor.
Observe que, em funcionamento normal, ambos os campos magnéticos do rotor e do estator $ B_{R} $ e $ B_{S} $ giram juntos na velocidade síncrona $ \eta_{sinc} $, ao passo que o próprio rotor gira a uma velocidade menor.
O campo magnético do rotor $ B_R $ gira na mesma velocidade que $ B_S $ apesar da frequência das grandezas elétricas do rotor serem diferentes das grandezas elétricas do estator.
A frequência elétrica das grandezas do rotor é exatamente a diferença entre a frequência das grandezas elétricas do rotor e da frequência de giro (mecânica) do rotor.
A soma da velocidade do rotor com a velocidade produzida pela frequência das grandezas do rotor faz com que a velocidade de $ B_R $ seja a mesma que $ B_S $.
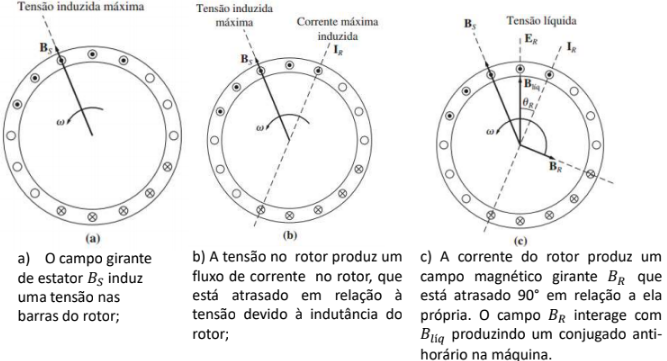
Conceito de escorregamento do rotor
A tensão induzida nas barras do rotor de um motor de indução depende da velocidade do rotor em relação aos campos magnéticos.
Duas variáveis são importantes. Uma delas é a velocidade de escorregamento e a outra o escorregamento.
$ \displaystyle \eta_{esc} = \eta_{sinc}-\eta_m $
$ \displaystyle s = \frac{\omega_{sinc}-\omega_m}{\omega_{sinc}} (\times100\%) \qquad s = \frac{\eta_{sinc}-\eta_m}{\eta_{sinc}} (\times100\%) $
$ \displaystyle \omega_m = (1-s)\,\omega_{sinc} \qquad \eta_m = (1-s)\,\eta_{sinc} $
A frequência elétrica no rotor
Um motor de indução trabalha induzindo tensões e correntes no rotor da máquina (transformador rotativo).
Para $ \eta_m = 0 $ rpm, a frequência do rotor é $ f_{re} = f_{se} $ e o escorregamento é $ s = 1 $. Para $ \eta_m = \eta_{sinc} $, a frequência do rotor é $ f_{re} = 0 $ Hz e o escorregamento é $ s = 0 $.
$ \displaystyle f_{re} = sf_{se} $
$ \displaystyle f_{re} = \frac{\eta_{sinc}-\eta_m}{\eta_{sinc}}f_{se} $
Circuito equivalente
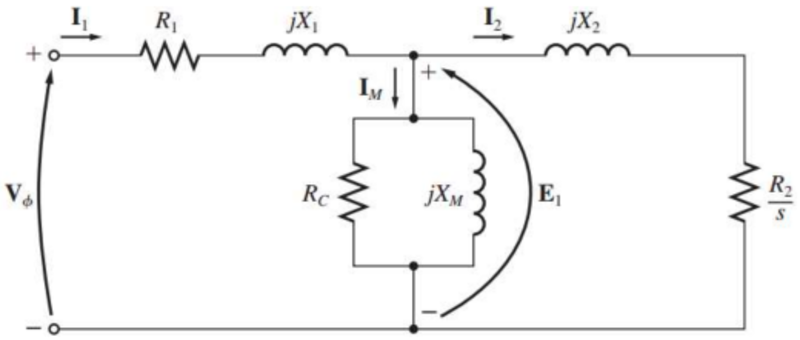
O circuito equivalente de um motor de indução é muito semelhante ao circuito equivalente de um transformador.
O circuito equivalente por fase de um transformador, representando o funcionamento de um motor de indução é apresentado abaixo
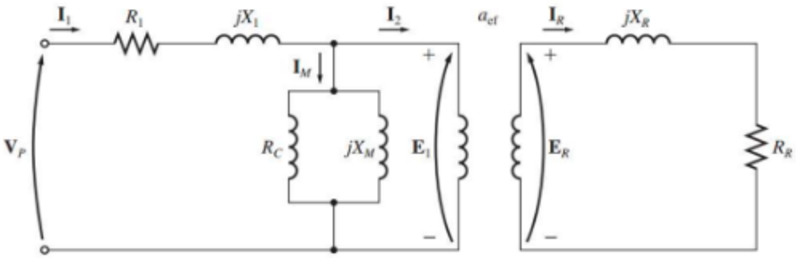
A tensão interna primária $ E_1 $ do estator está acoplada à tensão do secundário $ E_R $ por meio de um transformador ideal com uma relação de espiras efetivas $ a_{ef} $.
No caso de um motor com rotor de gaiola de esquilo, é bem difícil ver claramente $ a_{ef} $, por não há enrolamentos visíveis na gaiola de esquilo do rotor.
A reatância do rotor de um motor de indução depende da indutância do rotor e da frequência da tensão e da corrente do rotor. Com uma indutância de rotor $ L_R $, a reatância do rotor é dada por
$ \displaystyle X_R = \omega_{re}L_R = 2\pi f_{re}L_R = sX_{R0} $
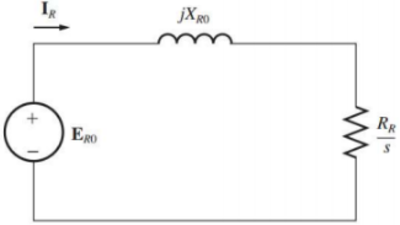
Onde $ X_{R0} $ e $ E_{R0} $ é a reatância e a tensão do rotor bloqueado.
O circuito equivalente resultante do rotor está mostrando abaixo

$ \displaystyle Z_{R,eq} = R_R\frac{1}{s}+jX_{R0} $
$ \displaystyle I_R = \frac{E_R}{R_R+jX_R} = \frac{E_R}{R_R+jsX_{R0}} = \frac{E_R}{R_R / s+jX_{R0}} $
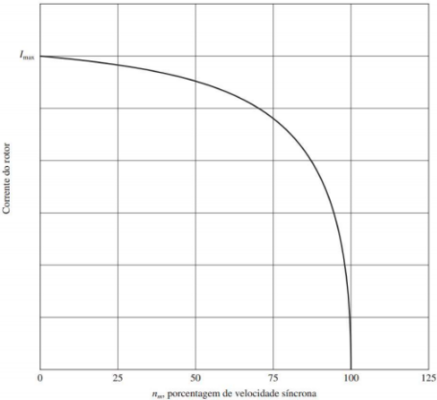
Para um escorregamento muito baixo, observe que o termo resistivo vale a expressão $ R_R / s >> X_{R0} $, de modo que a resistência do rotor predomina e a corrente do rotor varia linearmente com o escorregamento.
Com um escorregamento elevado, $ X_{R0} $ é muito maior do que $ R_R / s $ e a corrente do rotor aproxima-se de um valor de regime permanente à medida que o escorregamento torna-se muito elevado.
A resistência do rotor $ R_R $ e a reatância do rotor $ X_{R0} $, com o rotor bloqueado, são de determinação muito difícil ou impossível em rotores de gaiola de esquilo.
A relação de espiras efetiva $ a_{ef} $ também é de difícil obtenção no caso de rotores de gaiola de esquilo.
Felizmente, contudo, é possível realizar medidas que darão diretamente a resistência e a reatância referidas $ R_2 $ e $ X_2 $, mesmo que $ R_2 $ e $ X_{R0} $ e $ a_{ef} $ não sejam conhecidas separadamente.
$ \displaystyle Z_2 = a_{ef}^2 \left( \frac{R_R}{s}+jX_{R0} \right) $
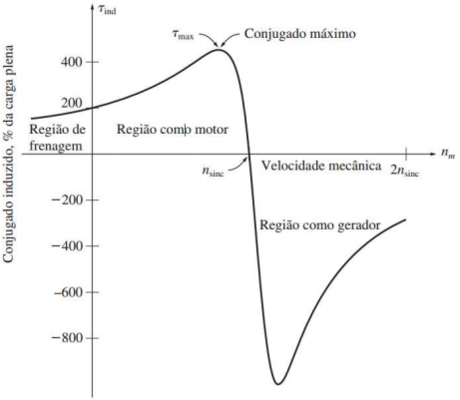
Conjugado versus velocidade
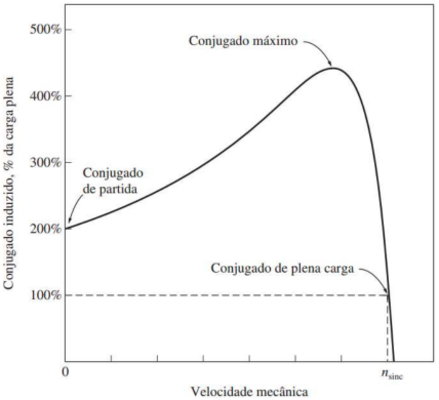
O conjugado induzido do motor é zero na velocidade síncrona.
A curva de conjugado versus velocidade é aproximadamente linear entre carga e vazio plena carga. $ (R_R >> X_R) $
Há um conjugado máximo possível que não pode ser excedido. Esse conjugado, denominado conjugado máximo, é 2 a 3 vezes o conjugado nominal de plena carga do motor.
O conjugado de partida do motor é ligeiramente superior a seu conjugado de plena carga, de modo que esse motor colocará em movimento qualquer carga que ele puder acionar a plena potência.
Observe que o conjugado do motor para um dado escorregamento varia com o quadrado da tensão aplicada (equação do conjugado).
$ \displaystyle \tau_{ind} = \frac{3V_{TH}^2R_2 / s}{\omega_{sinc}[(R_{TH}+R_2 / s)^2 + (X_{TH}+X_2)^2]} $
Se o rotor do motor de indução for acionado mais rapidamente do que a velocidade síncrona, então o sentido do conjugado induzido inverte-se e a máquina torna-se um gerador.
Controle da velocidade da máquina
A velocidade da máquina $ \omega_m $ é dada por
$ \displaystyle \omega_m = \frac{\omega_r}{P} = \omega_S-\omega_R $
onde,
$ \qquad \omega_r \rightarrow $ Velocidade elétrica.
$ \qquad P \rightarrow $ Número de pares de polos.
$ \qquad \omega_S \rightarrow $ Frequência das correntes estatóricas.
$ \qquad \omega_R \rightarrow $ Frequência das correntes rotóricas.
A velocidade mecânica pode ser alterada variando-se a frequência das correntes estatóricas $ \omega_S $ ou a frequência das correntes rotóricas $ \omega_R $.
Na máquina de rotor bobinado há a possibilidade de alterar $ \omega_m $ a partir de $ \omega_R $.
Isto é feito em sistemas de geração eólica com DFIG (Doubly Fed Induction Generator).
A grande maioria dos acionamentos modernos da máquina assíncrona se servem da variação da frequência estatórica para o controle da velocidade da máquina (inversor de frequência).
Para se definir um sistema de controle de velocidade da máquina é necessário analisar o modelo dinâmico da máquina.
Este modelo é complexo e não linear.
Antigamente o controle desse tipo de máquina era feito de forma escalar e considerava os modelos de regime da máquina.
Com o controle vetorial é possível realizar o controle dessa máquina de forma similar ao controle da máquina contínua.
Para que seja possível o controle vetorial da máquina é necessário que a alimentação da máquina seja feita com amplitude e frequência controladas.
Dessa forma o VSI é geralmente utilizado para acionar a máquina de indução sendo comandado por sinais PWM.

Um motor CC adiciona carga mecânica ao motor de indução.
A aquisição das variáveis, o controle e o comando são realizados por dispositivos de controle (DSPs, Dspaces, Arduinos).
Modelos dinâmicos da máquina de indução
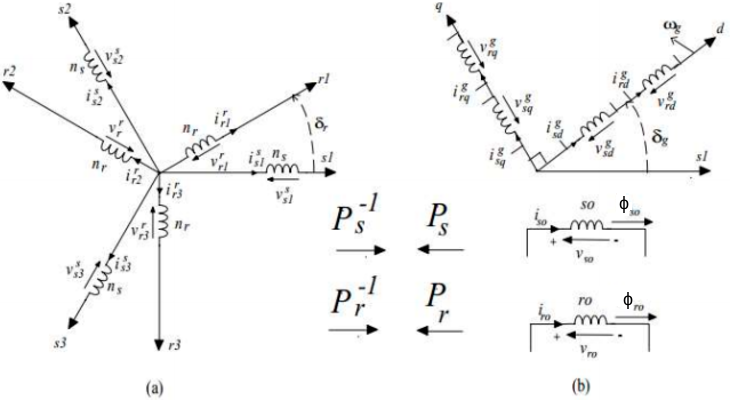
O modelo usualmente usado é obtido a partir de transformação de referencial.
$ \displaystyle \begin{cases} x_{s123} = P(\delta_g)x_{s0dq} \qquad \\ x_{r123} = P(\delta_g-\delta_r)x_{r0dq} \end{cases} $
onde,
$ \qquad x_{s123} \rightarrow $ Grandezas estatóricas no referencial natural.
$ \qquad x_{s0dq} \rightarrow $ Grandezas estatóricas no novo referencial.
$ \qquad x_{r123} \rightarrow $ Grandezas rotóricas no referencial natural.
$ \qquad x_{r0dq} \rightarrow $ Grandezas rotóricas no novo referencial.
$ \qquad P(\delta_g) \rightarrow $ Matriz de transformação para o referencial estator.
$ \qquad P(\delta_g-\delta_r) \rightarrow $ Matriz de transformação para o referencial rotor.
$ \qquad \delta_g \rightarrow $ Ângulo de transformação para o referencial estator.
$ \displaystyle P(\delta_p)
=
\sqrt{\frac{2}{3}}
\begin{bmatrix}
{\frac{1}{\sqrt{2}}} & \cos(\delta_p) & -\sin(\delta_p) \\
{\frac{1}{\sqrt{2}}} & \cos(\delta_p-\frac{2\pi}{3}) & -\sin(\delta_p-\frac{2\pi}{3}) \\
{\frac{1}{\sqrt{2}}} & \cos(\delta_p+\frac{2\pi}{3}) & -\sin(\delta_p+\frac{2\pi}{3})
\end{bmatrix} $
onde,
$ \qquad \delta_p \rightarrow $ Ângulo de transformação genérico.
$ \qquad \delta_p = \delta_g \rightarrow $ Transformação para grandezas estatóricas.
$ \qquad \delta_p = \delta_g-\delta_r \rightarrow $ Transformação para grandezas rotóricas.
Considerando que as bobinas são ligadas em estrela sem conexão com o neutro a componente homopolar pode ser desconsiderada.
Desta forma a máquina pode ser representada pelas variáveis $ dq $.
Com a representação $ 0dq $ os parâmetros da máquina de indução são constantes.
As indutâncias mútuas não dependem da posição rotórica.
No modelo $ dq $ a relação fluxo-corrente é dada por eixos magnéticos independentes e ortogonais.
A ortogonalidade faz com que o fluxo mútuo entre os dois eixos seja nulo.
Apesar dos eixos serem desacoplados existe um acoplamento no modelo da tensão em funçao das correntes e/ou fluxos.
Tal efeito é semelhante ao modelo da máquina CC onde os fluxos da máquina dependem apenas de suas correntes mas a tensão da armadura depende da excitação.
$ \displaystyle v_a = r_ai_a+l_a \frac{di_a}{dt}+e_a $
$ \displaystyle e_a = k_e\,\phi_e\,\omega_r $
Considerando que a máquina de indução é simétrica, livre de saturação e com distribuição senoidal de fluxo, temos o seguinte modelo genérico “$g$”.
| Grandezas estatórica e rotóricas no referencial $ dq $ |
| $ x_s^g = x_{sd}^g+jx_{sq}^g $ $ x_r^g = x_{rd}^g+jx_{rq}^g $ |
| LKM para o estator e o rotor |
| $ v_s^g = r_si_s^g+\frac{d\phi_s^g}{dt}+j\omega_g\phi_s^g \quad\qquad $ $ \,\, 0 = r_ri_r^g+\frac{d\phi_r^g}{dt}+j(\omega_g-\omega_g)\phi_r^g $ |
| Fluxo magnético no estator e no rotor |
| $ \phi_s^g = l_si_s^g+l_mi_r^g $ $ \phi_r^g = l_ri_r^g+l_mi_s^g $ |
| Modelo mecânico |
| $ P(c_e-c_m) = J\frac{d\omega_r}{dt}+F\omega_r $ |
| Conjugado elétrico da máquina |
| $ c_e = P\,i_s\,\phi_s\sin(\delta_i-\delta_a) = P\,\frac{l_m}{l_r}\,i_s\,\phi_r\sin(\delta_i-\delta_b) $ |
Características físicas da máquina
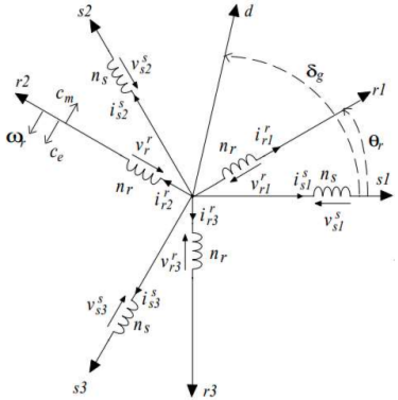
Para compreendermos o modelo anterior, é necessário que as características físicas da máquina, que estão no referencial $ 123 $, sejam definidas.
A resolução analítica de modelos que possuam elementos acoplados é penosa.
Isto se torna mais preocupante quando os coeficientes das equações diferenciais são em função do tempo.
Por este motivo as transformação de referencial são usadas na modelagem na máquina.
Para realizarmos a modelagem da máquina de indução, devemos seguir algumas considerações
- A máquina é simétrica em relação ao estator e ao rotor.
- Ângulos elétricos entre as bobinas de 120 graus.
- Correntes positivas geram fluxos positivos.

- Máquina como receptor.
- $ \theta_r = \frac{P}{2}\theta_m $
- Distribuição senoidal do fluxo magnético.
- Entreferro constante, relutância do entreferro independe de $ \theta_m $ (máquina de polos lisos).
- A máquina não está na sua região de saturação.
$ \phi_t = \sum\phi_i \qquad $ e $ \displaystyle \qquad c_e = \frac{dW}{d\theta_m} $
A notação utilizada na modelagem da máquina é a seguinte
$ \displaystyle X_y^z $
onde,
$ \qquad x \rightarrow $ Variável da máquina (tensão, corrente, fluxo, etc.)
$ \qquad y \rightarrow $ Localização física da variável (rotor, estator, enrolamentos, etc.)
$ \qquad z \rightarrow $ referencial onde a variável será modelada.
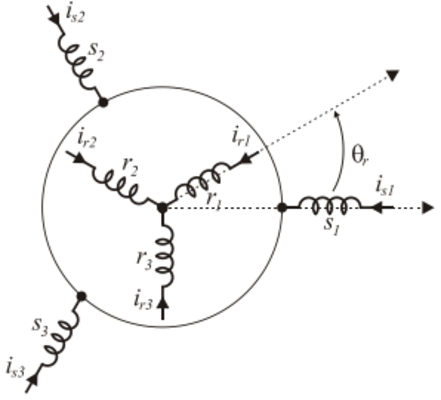
Com base nas hipóteses as grandezas físicas da máquina são representadas por
| Resistência dos enrolamento do estator e do rotor |
| $ R_{s1} = R_{s2} = R_{s3} = R_s $ $ R_{r1} = R_{r2} = R_{r3} = R_r $ |
| Indutâncias dos enrolamentos do estator e do rotor |
| $ L_{s1} = L_{s2} = L_{s3} = L_s $ $ L_{r1} = L_{r2} = L_{r3} = L_r $ |
| Indutâncias mútuas entre dois enrolamentos estatóricos e dois enrolamentos rotóricos |
| $ M_{s12} = M_{s23} = M_{s31} = M_s $ $ M_{r12} = M_{r23} = M_{r31} = M_r $ |
| Indutâncias mútuas entre os enrolamentos estatóricos e rotóricos |
| $ M_{sr}\cos(\theta_{sr}) = M_{rs}\cos(\theta_{rs}) $ |
onde as indutâncias mútuas estator-rotor são obtidas pela projeção da fase estatórica na rotórica, ou seja
| Entre os enrolamentos $ s_1 $ e $ r_{123} $ |
| $ M_{s1r1} = M_{sr}\cos{ \left( \theta_{r} \right) } \qquad\,\, $ $ M_{s1r2} = M_{sr}\cos{ \left( \theta_{r}+\frac{2\pi}{3} \right) } $ $ M_{s1r3} = M_{sr}\cos{ \left( \theta_{r}+\frac{4\pi}{3} \right) } $ |
| Entre os enrolamentos $ s_2 $ e $ r_{123} $ |
| $ M_{s2r1} = M_{sr}\cos{ \left( \theta_{r}+\frac{4\pi}{3} \right) } $ $ M_{s2r2} = M_{sr}\cos{ \left( \theta_{r} \right) } \qquad\,\, $ $ M_{s2r3} = M_{sr}\cos{ \left( \theta_{r}+\frac{2\pi}{3} \right) } $ |
| Entre os enrolamentos $ s_3 $ e $ r_{123} $ |
| $ M_{s3r1} = M_{sr}\cos{ \left( \theta_{r}+\frac{2\pi}{3} \right) } $ $ M_{s3r2} = M_{sr}\cos{ \left( \theta_{r}+\frac{4\pi}{3} \right) } $ $ M_{s3r3} = M_{sr}\cos{ \left( \theta_{r} \right) } \qquad\,\, $ |
Equações dos fluxos
Na forma matricial, as equações dos fluxos estatóricos e rotóricos podem ser escritas como
$ \displaystyle {\phi_{s123}^s}={{\bar{L}_{ss}}{i_{s123}^s}}+{{\bar{L}_{sr}}{i_{r123}^r}} $
$ \displaystyle {\phi_{r123}^r}={{\bar{L}_{rs}}{i_{s123}^s}}+{{\bar{L}_{rr}}{i_{r123}^r}} $
onde,
| Fluxos no estator e no rotor |
| $ \displaystyle \phi_{s123}^s=\begin{bmatrix} \phi_{s1}^s \\ \phi_{s2}^s \\ \phi_{s3}^s \end{bmatrix} \qquad \phi_{r123}^r=\begin{bmatrix} \phi_{r1}^r \\ \phi_{r2}^r \\ \phi_{r3}^r \end{bmatrix} $ |
| Correntes no estator e no rotor |
| $ \displaystyle i_{s123}^s=\begin{bmatrix} i_{s1}^s \\ i_{s2}^s \\ i_{s3}^s \end{bmatrix} \qquad i_{r123}^r=\begin{bmatrix} i_{r1}^r \\ i_{r2}^r \\ i_{r3}^r \end{bmatrix} $ |
| Indutâncias entre as fases do estator |
| $ \displaystyle \bar{L}_{ss} = \begin{bmatrix} L_s & M_s & M_s \\ M_s & L_s & M_r \\ M_s & M_s & L_s \end{bmatrix} $ |
| Indutâncias entre as fases do rotor |
| $ \displaystyle \bar{L}_{rr} = \begin{bmatrix} L_r & M_r & M_r \\ M_r & L_r & M_r \\ M_r & M_r & L_r \end{bmatrix}$ |
| Indutâncias entre as fases do estator e do rotor |
| $ \displaystyle \bar{L}_{sr} = M_{sr}\begin{bmatrix} \cos(\theta_r) & \cos(\theta_r+2\pi / 3) & \cos(\theta_r+4\pi / 3) \\ \cos(\theta_r+4\pi / 3) & \cos(\theta_r) & \cos(\theta_r+2\pi / 3) \\ \cos(\theta_r+2\pi / 3) & \cos(\theta_r+4\pi / 3) & \cos(\theta_r) \end{bmatrix} $ |
| Indutâncias entre as fases do rotor e do estator |
| $ \displaystyle \bar{L}_{rs} = M_{sr}\begin{bmatrix} \cos(\theta_r) & \cos(\theta_r+4\pi / 3) & \cos(\theta_r+2\pi / 3) \\ \cos(\theta_r+2\pi / 3) & \cos(\theta_r) & \cos(\theta_r+4\pi / 3) \\ \cos(\theta_r+4\pi / 3) & \cos(\theta_r+2\pi / 3) & \cos(\theta_r) \end{bmatrix} $ |
As matrizes apresentadas anteriormente possuem as seguintes propriedades
- $ L_{ss} $ e $ L_{rr} $ são matrizes simétricas.
- $ L_{sr}(\theta_r) $ e $ L_{rs}(\theta_r) $ são matrizes circulantes, isto é, $ x_{i,j} = x_{i+1,j+1} $.
- $ L_{sr}(\theta_r) = L_{rs}(\theta_r)^T $ uma matriz é a transposta da outra.
O sistema de equações dado anteriormente pode ainda ser escrito de forma mais compacta,
$ \displaystyle \bar{\phi}=\bar{L}\,\bar{i} $
onde,
$ \displaystyle \bar{\phi}
=
\begin{bmatrix}
\phi_{s123}^s & \phi_{r123}^r
\end{bmatrix}^T $
$ \displaystyle \bar{i}
=
\begin{bmatrix}
i_{s123}^s & i_{r123}^r
\end{bmatrix}^T $
$ \displaystyle \bar{L}
=
\begin{bmatrix}
L_{ss} & L_{sr} \\
L_{rs} & L_{rr}
\end{bmatrix} $
Equações das tensões
As orientações das bobinas são de tal forma que uma corrente positiva cria um fluxo positivo, assim
$ \displaystyle E_{fcem} = \frac{d\phi}{dt} $
onde,
$ \qquad E_{fcem} \rightarrow $ Tensão induzida nos terminais da bobina.
A $ fcem $ nos enrolamentos do estator e do rotor podem ser calculada como
$ \displaystyle \frac{d\phi_{s123}^s}{dt} = \frac{d}{dt}[\bar{L}_{ss}i_{s123}^s+\bar{L}_{sr}(\theta_r)i_{r123}^r] $
$ \displaystyle \frac{d\phi_{r123}^r}{dt} = \frac{d}{dt}[\bar{L}_{rs}i_{s123}^s+\bar{L}_{rr}(\theta_r)i_{r123}^r] $
Utilizando-se a conversão receptor e introduzindo as perdas resistivas,
$ \displaystyle V = Ri+\frac{d\phi}{dt} $
Sabendo determinar os fluxos magnéticos no estator e no rotor $ (\phi_{s123}^s $ e $ \phi_{r123}^r) $ e que
$ \displaystyle \frac{da(t)b(t)}{dt} = a(t)\frac{db(t)}{dt}+b(t)\frac{da(t)}{dt} $
temos,
$ \displaystyle {v_ {s123}^s}= R_si_{s123}^s+\bar{L}_{ss}\frac{di_{s123}^s}{dt}+\bar{L}_{sr}(\theta_r)\frac{di_{r123}^r}{dt}+\omega_r \left[\frac{d\bar{L}_{sr}(\theta_r)}{d\theta_r}\right] i_{r123}^r $
$ \displaystyle {v_ {r123}^r} = R_ri_{r123}^r+\bar{L}_{rr}\frac{di_{r123}^r}{dt}+\bar{L}_{rs}(\theta_r)\frac{di_{s123}^s}{dt}+\omega_r \left[\frac{d\bar{L}_{rs}(\theta_r)}{d\theta_r}\right] i_{s123}^s $
onde,
| Resistência nos enrolamentos do estator |
| $ \displaystyle R_s=\begin{bmatrix} R_s & 0 & 0 \\ 0 & R_s & 0 \\ 0 & 0 & R_s \end{bmatrix} $ |
| Resistência nos enrolamentos do rotor |
| $ \displaystyle R_r=\begin{bmatrix} R_r & 0 & 0 \\ 0 & R_r & 0 \\ 0 & 0 & R_r \end{bmatrix} $ |
| Tensão induzida de transformação no estator |
| $ \displaystyle \bar{L}_{ss}\frac{di_{s123}^s}{dt}+\bar{L}_{sr}(\theta_r)\frac{di_{r123}^r}{dt} $ |
| Tensão induzida de transformação no rotor |
| $ \displaystyle \bar{L}_{rr}\frac{di_{r123}^r}{dt}+\bar{L}_{rs}(\theta_r)\frac{di_{s123}^s}{dt} $ |
| Tensão induzida de rotação do rotor no estator |
| $ \displaystyle \omega_r\left[ \frac{d\bar{L}_{sr}}{d\theta_r} \right]i_{r123}^r $ |
| Tensão induzida de rotação do rotor no rotor |
| $ \displaystyle \omega_r\left[ \frac{d\bar{L}_{rs}}{d\theta_r} \right]i_{s123}^s $ |
| Velocidade rotórica |
| $ \displaystyle \omega_r = \frac{d\theta_r}{dt} $ |
De forma mais compacta
$ \displaystyle \bar{v} = \bar{R}\bar{i}+\bar{L}\frac{d\bar{i}}{dt}+\omega_r\left[\frac{d\bar{L}}{dt}\right]\bar{i} $
onde,
$ \displaystyle \bar{v}
=
\begin{bmatrix}
v_{s123}^s & v_{r123}^r
\end{bmatrix}^T $
$ \displaystyle \bar{R}
=
\begin{bmatrix}
\bar{R}_s & 0 \\ 0 & \bar{R}_r
\end{bmatrix} = \begin{bmatrix}
R_sI_3 & 0 \\ 0 & R_rI_3
\end{bmatrix} $
Equações do conjugado
A expressão geral da energia é dada por
$ \displaystyle W = \frac{1}{2}\bar{i}^T\bar{L}\bar{i} $
O conjugado é obtido derivando-se a expressão da energia, obtém-se que
$ \displaystyle c_e=\frac{dW}{d\theta_m} $
assumindo que,
$ \displaystyle \theta_m = \theta_r/P $
temos,
$ \displaystyle c_e=P\frac{dW}{d\theta_r} $
Assim, derivando-se a expressão da energia, obtém-se que
$ \displaystyle c_e = \frac{P}{2}\bar{i}^T\left[\frac{d\bar{L}}{d\theta_r} \right]\bar{i} $
Como as submatrizes $ L_{ss} $ e $ L_{rr} $ são independentes do ângulo rotórico,
$ \displaystyle c_e = \frac{P}{2} \begin{bmatrix} i_{s123}^s \\ i_{r123}^r \end{bmatrix}^T \begin{bmatrix} 0 & \frac{d\bar{L}_{sr}}{d\theta_r} \\ \frac{d\bar{L}_{rs}}{d\theta_r} & 0 \end{bmatrix} \begin{bmatrix} i_{s123}^s \\ i_{r123}^r \end{bmatrix} $
$ \displaystyle c_e = \frac{P}{2} {i_{s123}^s}^T \left[ \frac{d\bar{L}_{sr}}{d\theta_r} \right] i_{r123}^r + \frac{P}{2} {i_{r123}^r}^T \left[ \frac{d\bar{L}_{rs}}{d\theta_r} \right] i_{s123}^s $
Como $ c_e^T = c_e $, $ (A+B)^T = A^T+B^T $ e $ (ABC)^T = C^TB^TA^T $
$ \displaystyle c_e^T = \frac{P}{2} {i_{r123}^r}^T \left[ \frac{d\bar{L}_{sr}}{d\theta_r} \right]^T i_{s123}^s + \frac{P}{2} {i_{s123}^s}^T \left[ \frac{d\bar{L}_{rs}}{d\theta_r} \right]^T i_{r123}^r $
$ \displaystyle \frac{P}{2} {i_{s123}^s}^T \left[ \frac{d\bar{L}_{sr}}{d\theta_r} \right] i_{r123}^r = \frac{P}{2} {i_{r123}^r}^T \left[ \frac{d\bar{L}_{rs}}{d\theta_r} \right] i_{s123}^s $
como $ \bar{L}_{sr} = \bar{L}_{rs}^T $
$ \displaystyle c_e = P \, {i_{s123}^s}^T \left[ \frac{d\bar{L}_{sr}}{d\theta_r} \right] i_{r123}^r $
ou
$ \displaystyle c_e = P \, {i_{r123}^r}^T \left[ \frac{d\bar{L}_{sr}}{d\theta_r} \right] i_{s123}^s $
Equações da potência instantânea
$ \displaystyle p=\bar{i}^T\bar{v} $
$ \displaystyle p=\bar{R}\bar{i}\bar{R}^T+\bar{i}^T \bar{L}\frac{d\bar{i}}{dt}+\omega_r\bar{i}^T\left[\frac{d\bar{L}}{dt}\right]\bar{i} $
onde,
| Potência de transformação | $ \displaystyle \bar{i}^T \bar{L}\frac{d\bar{i}}{dt} $ |
| Potência de rotação | $ \displaystyle \omega_r\bar{i}^T\left[\frac{d\bar{L}}{dt}\right]\bar{i} $ |
Equações finais da máquina
O modelo dinâmico da máquina trifásica pode então ser representado pelo seguinte conjunto de equações
| Tensões no estator e no rotor |
| $ \displaystyle v_{s123}^s = R_si_{s123}^s+\bar{L}_{ss}\frac{di_{s123}^s}{dt}+\bar{L}_{sr}(\theta_r)\frac{di_{r123}^r}{dt}+\omega_r \left[\frac{d\bar{L}_{sr}(\theta_r)}{d\theta_r}\right] i_{r123}^r $ $ \displaystyle v_{r123}^r = R_ri_{r123}^r+\bar{L}_{rr}\frac{di_{r123}^r}{dt}+\bar{L}_{rs}(\theta_r)\frac{di_{s123}^s}{dt}+\omega_r \left[\frac{d\bar{L}_{rs}(\theta_r)}{d\theta_r}\right] i_{s123}^s $ |
| Fluxos magnéticos no estator e no rotor |
| $ \displaystyle \phi_{s123}^s = \bar{L}_{ss}i_{s123}^s+\bar{L}_{sr}i_{r123}^r $ $ \displaystyle \phi_{r123}^r = \bar{L}_{rs}i_{s123}^s+\bar{L}_{rr}i_{r123}^r $ |
| Conjugado elétrico |
| $ \displaystyle c_e = P \, {i_{s123}^s}^T \left[ \frac{d\bar{L}_{sr}}{d\theta_r} \right] i_{r123}^r $ |
Aplicações das máquinas de indução. (a) Ventilador. (b) Carro Elétrico. (c) Resolver.
Referências
- Notas de aula do prof. dr. Caio Dorneles Cunha e prof. dr. Thiago de Oliveira Alves Rocha.
- Mohan, Undeland e Robbins, Power Electronics. Willey, 1989.
- W. Leonard, Control of Electrical Drives. Springer, 2001 2Ed.
- M. E. El-Hawary, Modeling and High Performance Control of Electric Machines. John Wiley & Sons, 2005.
- Chen-Mun Ong, Dynamic Simulation of Electric Machinery. Prentice-Hall, 1997.
- R. Krishnan, Eletric Motor Drives, Modeling, Analysis, and Control. Prentice-Hall, 2001.
- Ned Mohan, Máquinas Elétricas e Acionamentos. LTC, 2015.
- Ivo Barbi, Teoria Fundamental do Motor de Indução. Editora da UFSC/ELETROBRÁS, 1985.
