A velocidade da máquina $ \omega_m $ é dada por
$ \displaystyle {\omega_m}=\frac{\omega_r}{P}={{\omega_S}-{\omega_R}} $
onde,
$ \qquad \omega_r \rightarrow $ Velocidade elétrica.
$ \qquad P \rightarrow $ Número de pares de polos.
$ \qquad \omega_S \rightarrow $ Frequência das correntes estatóricas.
$ \qquad \omega_R \rightarrow $ Frequência das correntes rotóricas.
A velocidade mecânica pode ser alterada variando-se a frequência das correntes estatóricas $ \omega_S $ ou a frequência das correntes rotóricas $ \omega_R $.
Na máquina de rotor bobinado há a possibilidade de alterar $ \omega_m $ a partir de $ \omega_R $.
Isto é feito em sistemas de geração eólica com DFIG (Doubly Fed Induction Generator).
A grande maioria dos acionamentos modernos da máquina assíncrona se servem da variação da frequência estatórica para o controle da velocidade da máquina (inversor de frequência).
Para se definir um sistema de controle de velocidade da máquina é necessário analisar o modelo dinâmico da máquina.
Este modelo é complexo e não linear.
Antigamente o controle desse tipo de máquina era feito de forma escalar e considerava os modelos de regime da máquina.
Com o controle vetorial é possível realizar o controle dessa máquina de forma similar ao controle da máquina contínua.
Para que seja possível o controle vetorial da máquina é necessário que a alimentação da máquina seja feita com amplitude e frequência controladas.
Dessa forma o VSI é geralmente utilizado para acionar a máquina de indução sendo comandado por sinais PWM.
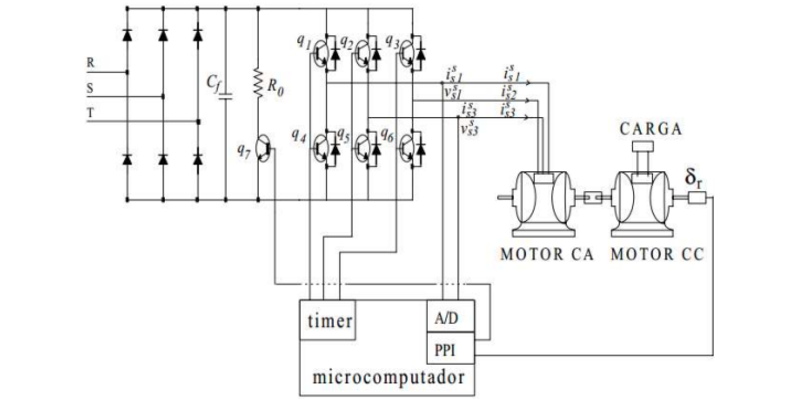
Um motor CC adiciona carga mecânica ao motor de indução.
A aquisição das variáveis, o controle e o comando são realizados por dispositivos de controle (DSPs, Dspaces, Arduinos).
Máquina CA no referencial 0dq
Considerando $ \bar{P}_s $ a matriz de transformação para o estator e $ \bar{P}_r $ para o rotor
$ \displaystyle {x_{s123}^s}={{\bar{P}_s}{x_{s0dq}^g}} $
$ \displaystyle {x_{r123}^r}={\bar{P}_r}{x_{r0dq}^g} $
Estator $ g \rightarrow s $, rotor $ g \rightarrow r $ e campo girante $ \rightarrow e $
$ \bar{P}_s = \sqrt{\frac{2}{3}} \begin{bmatrix}
{\frac{1}{\sqrt{2}}} & \cos(\delta_g) & -\sin(\delta_g) \\
{\frac{1}{\sqrt{2}}} & \cos(\delta_g-\frac{2\pi}{3}) & -\sin(\delta_g-\frac{2\pi}{3}) \\
{\frac{1}{\sqrt{2}}} & \cos(\delta_g+\frac{2\pi}{3}) & -\sin(\delta_g+\frac{2\pi}{3})
\end{bmatrix} \qquad\qquad\, $
$ \bar{P}_r = \sqrt{\frac{2}{3}} \begin{bmatrix}
{\frac{1}{\sqrt{2}}} & \cos(\delta_g-\theta_r) & -\sin(\delta_g-\theta_r) \\
{\frac{1}{\sqrt{2}}} & \cos(\delta_g-\theta_r-\frac{2\pi}{3}) & -\sin(\delta_g-\theta_r-\frac{2\pi}{3}) \\
{\frac{1}{\sqrt{2}}} & \cos(\delta_g-\theta_r+\frac{2\pi}{3}) & -\sin(\delta_g-\theta_r+\frac{2\pi}{3})
\end{bmatrix} $
$ \bar{P}_s^{-1}=\bar{P}_s^T \qquad $ e $ \qquad \bar{P}_r^{-1}=\bar{P}_r^T $
Grandezas elétricas do estator giram com a velocidade $ \omega_g $ e ângulo $ \delta_g $
Grandezas elétricas do rotor giram com a velocidade $ \omega_g-\omega_r $ e ângulo $ \delta_g-\theta_r $
Equação dos fluxos magnéticos em 0dq
No estator
$ {\lambda_{s123}^s}={{{\bar{L}_{ss}}{i_{s123}^s}}+{{\bar{L}_{sr}}{i_{r123}^r}}} $
$ {{\bar{P}_s}{\lambda_{s0dq}^g}}={{{\bar{L}_{ss}}{\bar{P}_s}{i_{s0dq}^g}}+{{\bar{L}_{sr}}{\bar{P}_r}{i_{r0dq}^g}}} $
$ {\lambda_{s0dq}^g}={{\bar{P}_s^{-1}}{\bar{L}_{ss}}{\bar{P}_s}{i_{s0dq}^g}}+{{\bar{P}_s^{-1}}{\bar{L}_{sr}}{\bar{P}_r}{i_{r0dq}^g}} $
$ {\lambda_{s0dq}^g}={{\bar{L}_{ss0dq}}{i_{s0dq}^g}}+{{\bar{L}_{sr0dq}}{i_{r0dq}^g}} $
No rotor
$ {\lambda_{r123}^r}={{\bar{L}_{rs}}{i_{s123}^s}}+{{\bar{L}_{rr}}{i_{r123}^r}} $
$ {{\bar{P}_r}{\lambda_{r0dq}^g}}={{\bar{L}_{rs}}{\bar{P}_s}{i_{s0dq}^g}}+{{\bar{L}_{rr}}{\bar{P}_r}{i_{r0dq}^g}} $
$ {\lambda_{r0dq}^g}={{\bar{P}_r^{-1}}{\bar{L}_{rs}}{\bar{P}_s}{i_{s0dq}^g}}+{{\bar{P}_r^{-1}}{\bar{L}_{rr}}{\bar{P}_r}{i_{r0dq}^g}} $
$ \lambda_{r0dq}^r = \bar{L}_{rs0dq}i_{s0dq}^s+\bar{L}_{rr0dq}i_{r0dq}^r $
onde,
| Indutâncias entre as fases do estator | $ \bar{L}_{ss0dq} = \begin{bmatrix} L_s+2M_s & 0 & 0 \\ 0 & L_s-M_s & 0 \\ 0 & 0 & L_s-M_s \end{bmatrix} = \begin{bmatrix} l_{so} & 0 & 0 \\ 0 & l_s & 0 \\ 0 & 0 & l_s \end{bmatrix} $ |
| Indutâncias entre as fases do rotor | $ \bar{L}_{sr0dq} = \begin{bmatrix} L_r+2M_r & 0 & 0 \\ 0 & L_r-M_r & 0 \\ 0 & 0 & L_r-M_r \end{bmatrix} = \begin{bmatrix} l_{ro} & 0 & 0 \\ 0 & l_r & 0 \\ 0 & 0 & l_r \end{bmatrix} $ |
| Indutâncias entre as fases do estator e do rotor | $ \bar{L}_{sr0dq} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 2/3M_{sr} & 0 \\ 0 & 0 & 3/2L_r-M_r \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & l_m & 0 \\ 0 & 0 & l_m \end{bmatrix} \qquad\, $ |
| Indutâncias entre as fases do rotor e do estator | $ \bar{L}_{rs0dq} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 2/3M_{sr} & 0 \\ 0 & 0 & 3/2L_r-M_r \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & l_m & 0 \\ 0 & 0 & l_m \end{bmatrix} \qquad\, $ |
As matrizes de indutância independem dos ângulos $ \delta_g $ e $ \theta_r $.
$ l_s $, $ l_{so} $, l_r $, $ l_{ro} $ e $ l_m $ são denominados indutâncias cíclicas.
logo,
| Fluxo no estator | $ \phi_{sd}^g = l_si_ {sd}^g+l_mi_{rd}^g $ $ \phi_{sq}^g = l_si_ {sq}^g+l_mi_{rq}^g $ |
| Fluxo no rotor | $ \phi_{rd}^g = l_ri_ {rd}^g+l_mi_{sd}^g $ $ \phi_{rq}^g = l_ri_ {rq}^g+l_mi_{sq}^g $ |
Equação das tensões em 0dq
$ \displaystyle {v_{s123}^s}={{r_s}{i_{s123}^s}}+{\frac{d\lambda_{s123}^s}{dt}} \qquad\qquad\qquad\qquad\quad\, $
$ \displaystyle {v_{s0dq}^g}={{\bar{P}_s^{-1}}{r_s}{\bar{P}_s}{i_{s0dq}^g}}+ {\bar{P}_s^{-1}}{\frac{d\left[{\bar{P}_s}{\lambda_{s0dq}^g}\right]}{dt}} \qquad\, $
$ \displaystyle {v_{s0dq}^g}={{r_s}{i_{s0dq}^g}}+ {\bar{P}_s^{-1}}{\frac{d\left[{\bar{P}_s}{\lambda_{s0dq}^g}\right]}{dt}} \qquad\qquad\quad $
$ \displaystyle {v_{s0dq}^g}={{r_s}{i_{s0dq}^g}}+{\frac{d{\lambda_{s0dq}^g}}{dt}+{\bar{P}_s^{-1}}{\frac{d\bar{P}_s}{dt}}{\lambda_{s0dq}^g}} \qquad $
$ \displaystyle {v_{s0dq}^g}={{r_s}{i_{s0dq}^g}}+ {\frac{d{\lambda_{s0dq}^g}}{dt}}+{{\bar{P}_s^{-1}}}{\frac{d{\delta_g}}{d{\delta_g}}}{\frac{d{\bar{P}_s}}{dt}}{\lambda_{s0dq}^g} $
$ \displaystyle {v_{s0dq}^g}={{r_s}{i_{s0dq}^g}}+{\frac{d{\lambda_{s0dq}^g}}{dt}}+{{\omega_g}{\bar{P}_s^{-1}}}{\frac{d{\bar{P}_s}}{d{\delta_g}}}{\lambda_{s0dq}^g} \,\,\,\, $
$ \displaystyle {v_{s0dq}^g}={{r_s}{i_{s0dq}^g}}+{\frac{d{\lambda_{s0dq}^g}}{dt}}+{\omega_g}{\begin{bmatrix}
0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{bmatrix}}{\lambda_{s0dq}^g} \qquad $
De forma análoga, temos as tensões rotóricas
$ v_{r0dq}^g = r_r i_{r0dq}^g + \frac{d\lambda_{r0dq}^g}{dt}+(\omega_g-\omega_r)\begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0
\end{bmatrix}\lambda_{r0dq}^g $
logo,
| Tensões no estator | $ v_{sd}^g = r_si_{sd}^g + \frac{d\phi_{sd}^g}{dt}-\omega_g\phi_{sq}^g \qquad\quad $ $ v_{sq}^g = r_si_{sq}^g + \frac{d\phi_{sq}^g}{dt}+\omega_g\phi_{sd}^g \qquad\quad $ |
| Tensões no rotor | $ v_{rd}^g = r_ri_{rd}^g+\frac{d\phi_{rd}^g}{dt}-(\omega_g-\omega_r)\phi_{rq}^g $ $ v_{rq}^g = r_ri_{rq}^g + \frac{d\phi_{rq}^g}{dt}+(\omega_g-\omega_r)\phi_{rd}^g $ |
Substituindo as equações de fluxo nas tensões temos
| Tensões em d no estator e no rotor | $ v_{sd}^g = r_si_{sd}^g + l_{\sigma s}\frac{di_{sd}^g}{dt}+l_m\frac{d}{dt}(i_{sd}^g+i_{rd}^g)+\omega_g\phi_{sq}^g \qquad\quad $ $ v_{rd}^g = r_ri_{rd}^g + l_{\sigma r}\frac{di_{rd}^g}{dt}+l_m\frac{d}{dt}(i_{rd}^g+i_{sd}^g)+(\omega_g-\omega_r)\phi_{rq}^g \, $ |
| Tensões em q no estator e no rotor | $ v_{sq}^g = r_si_{sq}^g + l_{\sigma s}\frac{di_{sq}^g}{dt}+l_m\frac{d}{dt}(i_{sq}^g+i_{rq}^g)-\omega_g\phi_{sq}^g \qquad\quad $ $ v_{rq}^g = r_ri_{rq}^g + l_{\sigma r}\frac{di_{rq}^g}{dt}+l_m\frac{d}{dt}(i_{rq}^g+i_{sq}^g)+(\omega_g-\omega_r)\phi_{rd}^g \, $ |
onde,
$ l_{\sigma r} = l_m +l_r $

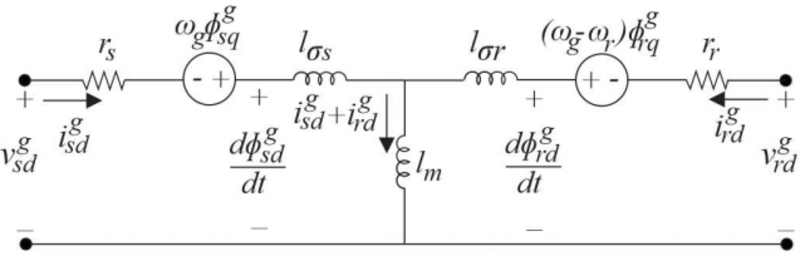
Circuito equivalente da máquina CA. (a) Grandezas em d. (b) Grandezas em q.
Equação do conjugado em 0dq
$ \displaystyle {c_e}={{P}{{i_{s123}^s}^T}{\left[{\frac{d{\bar{L}_{sr}}}{d{\theta_r}}}\right]}{i_{r123}^s}} \qquad\,\,\, $
$ \displaystyle {c_e}={{P}{{i_{s0dq}^g}^T}{\bar{P}_s^T}{\left[{\frac{d\bar{L}_{sr}}{d\theta_r}}\right]}{\bar{P}_r}{i_{r0dq}^g}} $
$ \displaystyle {c_e}={P}{l_m}{\left({{{i_{sq}^g}{i_{rd}^g}}-{{i_{sd}^g}{i_{rq}^g}}}\right)} \qquad\,\,\, $
Equação da potência em 0dq
$ p=\bar{i}^T\bar{v}=p_{s123}+p_{r123}={i_{s123}^s}^Tv_{s123}^s+{i_{r123}^r}^Tv_{r123}^r $
Se $ p_{s0dq} = {i_{s123}^g}^Tv_{s123}^g $, $ p_{s0dq} = p_{s123} $ se $ \bar{P}^T\bar{P} = 1 $
$ p_{s123} = {i_{s0dq}^g}^T\bar{P}^T\bar{P}v_{s0dq}^g $
Como $ \bar{P}^T\bar{P} = 1 $
$ {p_{s123}}={{{i_{sd}^g}{v_{sd}^g}}+{{i_{sq}^g}{v_{sq}^g}}+{{i_{s0}^g}{v_{s0}^g}}} $
Equações finais da máquina em $ 0dq $
Considerando que as componentes homopolares não produzem conjugado, então o modelo dinâmico da máquina equilibrada pode ser dado por
| Tensões no estator e no rotor | $ v_{sdq}^g = r_s i_{sdq}^g + \frac{d\lambda_{sdq}^g}{dt}+\omega_g\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}\lambda_{sdq}^g \qquad\quad $ $ v_{rdq}^g = r_r i_{rdq}^g + \frac{d\lambda_{rdq}^g}{dt}+(\omega_g-\omega_r)\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}\lambda_{rdq}^g $ |
| Fluxos magnéticos no estator e no rotor | $ \lambda_{sdq}^g = l_{s}i_{sdq}^g+l_{m}i_{rdq}^g $ $ \lambda_{rdq}^g = l_{r}i_{rdq}^g+l_{m}i_{sdq}^g $ |
| Conjugado elétrico | $ c_e = P \, l_m(i_{sq}^gi_{rd}^g-i_{sd}^gi_{rq}^g) $ |
Escolha da posição ou referencial para os eixos $ dq $
- No estator, com o eixo $ d $ sobre a fase $ s_1 $, fazendo-se $ \delta_g = 0 \, (\omega_g=0) $. Levando ao regime permanente, variáveis $ dq $ senoidais com mesma frequência das correntes estatóricas.
- No rotor, com o eixo d sobre a fase $ r_1 $, ou seja $ \delta_g = \theta_r(\omega_g=\omega_r) $. Levando ao regime permanente, variáveis $ dq $ senoidais com mesma frequência das correntes rotóricas ( $ \omega_{rs} = \omega_r-\omega_s $, frequência de escorregamento se a máquina for assíncrona e zero se for síncrona).
- No campo girante, fazendo $ \delta_g = \theta_s \, (\delta_g=\delta_s) $. Levando ao regime permanente, variáveis $ dq $ contínuas.


Do modelo natural da máquina CA e considerando que a máquina de indução é simétrica, livre de saturação e com distribuição senoidal de fluxo, temos o seguinte modelo genérico “g”.
| Modelo elétrico | $ v_s^g = r_si_s^g+\frac{d\phi_s^g}{dt}+j\omega_g\phi_s^g \qquad\qquad $ $ 0 = r_ri_r^g+\frac{d\phi_r^g}{dt}+j(\omega_g-\omega_r)\phi_r^g \,\,$ $ \phi_s^g = l_si_s^g+l_mi_r^g $ $ \phi_r^g = l_ri_r^g+l_mi_s^g $ |
| Modelo mecânico | $ P(c_e-c_m) = j\frac{d\omega_r}{dt}+F\omega_r $ |
Onde o conjugado elétrico da máquina é
$ \displaystyle {c_e}={{P}{i_s}{\phi_s}{\sin(\delta_i-\delta_a)}}={P}{\frac{l_m}{l_r}}{i_s}{\phi_r}{\sin(\delta_i-\delta_b)} $
A divisão do modelo em parte elétrica e mecânica é possível porque a dinâmica da parte mecânica tem dinâmica mais lenta que a elétrica.
Esse desacoplamento permite representar a máquina por um modelo linear variante no tempo, onde $ \omega_r $ comporta-se como parâmetro variável.
O modelo elétrico possui 4 variáveis de estado e duas equações.
A substituição das equações dos fluxos nas equações da tensões nos permite obter um sistema determinado.
Modelo dinâmico A: $ \phi_s \,-\, \phi_r $
Neste modelo os fluxos são as variáveis de estado.
Ele é obtido a partir das substituições das seguintes equações.
$ i_s^g = \frac{\phi_s^g-l_mi_r^g}{l_s} $
$ i_r^g = \frac{\phi_r^g-l_mi_s^g}{l_r} $
Nas equações da máquina
$ \displaystyle v_s^g = \frac{r_s}{\sigma l_s}\phi_s^g+\frac{d\phi_s^g}{dt}+j\omega_g\phi_s^g-\frac{l_mr_s}{\sigma l_sl_r}\phi_r^g \quad\qquad $
$ \displaystyle 0 = \frac{r_r}{\sigma l_s}\phi_r^g + \frac{d\phi_r^g}{dt}+j(\omega_g-\omega_r)\phi_r^g-\frac{l_m}{\sigma l_s \tau_r}\phi_s^g $
$ \displaystyle c_e = P\frac{l_m}{\sigma l_sl_r}\phi_s\phi_r\sin(\delta_a-\delta_b) \qquad\qquad\qquad\,\, $
onde,
| constante de tempo rotórica | $ \phi_r = \frac{l_r}{r_r} $ |
| coeficiente de dispersão da máquina | $ \sigma = 1-\frac{l_m^2}{l_sl_r} $ |
Modelo dinâmico B: $ i_s \,-\, \phi_r $
Neste modelo o fluxo rotórico e correntes estatóricas são as variáveis de estado.
Ele é o obtido a partir das substituições das seguintes equações
$ i_s^g = \frac{\phi_s^g-l_mi_r^g}{l_s} $
$ \phi_r^g = l_ri_r^g+l_mi_s^g $
Nas equações da máquina
logo,
$ \displaystyle v_s^g = \left(r_s+\frac{r_rl_m^2}{l_s^2}\right)i_s^g+\sigma l_s \frac{di_s^g}{dt}+j\omega_g\sigma l_si_s^g+\left( j\omega_r-\frac{1}{\tau_r} \right)\frac{l_m}{l_r}\phi_r^g $
$ \displaystyle 0 = \frac{1}{\tau_r}\phi_r^g+\frac{d\phi_r^g}{dt}+j(\omega_g-\omega_r)\phi_r^g-\frac{l_m}{\tau_r}i_s^g \qquad\qquad\qquad\qquad\,\,\, $
$ \displaystyle c_e = P\frac{l_m}{\sigma l_r}i_s\phi_r\sin(\delta_a-\delta_b) \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\, $
Modelo dinâmico C: $ i_s \,-\, i_{rm} $
Neste modelo as correntes estatóricas e a corrente de magnetização rotórica são as variáveis de estado.
Ele é o obtido a partir das substituições das seguintes equações
$ \displaystyle i_s^g = \frac{\phi_s^g-l_mi_r^g}{l_s} $
$ \displaystyle \phi_r = \phi_{rm}^g = l_mi_{rm}^g $
Nas equações da máquina
$ \displaystyle v_s^g = \left(r_s+\frac{l_s-\sigma l_s}{\tau_r}\right)i_s^g+\sigma l_s \frac{di_s^g}{dt}+j\omega_g\sigma l_si_s^g+\left( j\omega_r-\frac{1}{\tau_r} \right)(l_s-\sigma l_s)i_{rm}^g $
$ \displaystyle 0 = \frac{1}{\tau_r}i_{rm}^g+\frac{di_{rm}^g}{dt}+j(\omega_g-\omega_r)i_{rm}^g-\frac{i}{\tau_r}i_s^g \qquad\qquad\qquad\qquad\qquad\qquad $
$ \displaystyle c_e = P(l_s-\sigma l_s)i_si_{rm}\sin(\delta_i-\delta_b) \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad $
Referencial genérico $ \omega_g \, (x_{dq}^g) $
| Estator | $ v_{sd}^g = r_si_{sd}^g + \frac{d\phi_{sd}^g}{dt}-\omega_g\phi_{sq}^g $ $ v_{sq}^g = r_si_{sq}^g + \frac{d\phi_{sq}^g}{dt}+\omega_g\phi_{sd}^g $ $ \phi_{sd}^g = l_si_ {sd}^g+l_mi_{rd}^g $ $ \phi_{sq}^g = l_si_ {sq}^g+l_mi_{rq}^g $ |
| Rotor | $ v_{rd}^g = r_ri_{rd}^g+\frac{d\phi_{rd}^g}{dt}-(\omega_g-\omega_r)\phi_{rq}^g $ $ v_{rq}^g = r_ri_{rq}^g + \frac{d\phi_{rq}^g}{dt}+(\omega_g-\omega_r)\phi_{rd}^g $ $ \phi_{rd}^g = l_ri_ {rd}^g+l_mi_{sd}^g $ $ \phi_{rq}^g = l_ri_ {rq}^g+l_mi_{sq}^g $ |
Referencial estacionário $ \omega_g = 0\, (x_{dq}^g) $
| Estator | $ v_{sd}^g = r_si_{sd}^g + \frac{d\phi_{sd}^g}{dt} $ $ v_{sq}^g = r_si_{sq}^g + \frac{d\phi_{sq}^g}{dt} $ $ \phi_{sd}^g = l_si_ {sd}^g+l_mi_{rd}^g $ $ \phi_{sq}^g = l_si_ {sq}^g+l_mi_{rq}^g $ |
| Rotor | $ v_{rd}^g = r_ri_{rd}^g+\frac{d\phi_{rd}^g}{dt}+\omega_r\phi_{rq}^g $ $ v_{rq}^g = r_ri_{rq}^g + \frac{d\phi_{rq}^g}{dt}-\omega_r\phi_{rd}^g $ $ \phi_{rd}^g = l_ri_ {rd}^g+l_mi_{sd}^g $ $ \phi_{rq}^g = l_ri_ {rq}^g+l_mi_{sq}^g $ |
$ \displaystyle v_{sd}^s = r_si_{sd}^s + \sigma l_s\frac{di_{sd}^s}{dt} + \left[ -\frac{l_m}{l_ r}r_ri_{rd}^s-\omega_rl_mi_{rq}^s+\omega_r\frac{{l_m}^2}{l_r}i_{sq}^s\right] $
$ \displaystyle v_{sq}^s = r_si_{sq}^s + \sigma l_s\frac{di_{sq}^s}{dt} + \left[ -\frac{l_m}{l_ r}r_ri_{rq}^s+\omega_rl_mi_{rd}^s-\omega_r\frac{{l_m}^2}{l_r}i_{sd}^s\right] $
onde,
$ \displaystyle p_d^s = \left[ -\frac{l_m}{l_ r}r_ri_{rd}^s-\omega_rl_mi_{rq}^s+\omega_r\frac{{l_m}^2}{l_r}i_{sq}^s\right] $
$ \displaystyle p_q^s = \left[ -\frac{l_m}{l_ r}r_ri_{rq}^s+\omega_rl_mi_{rd}^s-\omega_r\frac{{l_m}^2}{l_r}i_{sd}^s\right] $
são perturbações a serem compensadas através de
$ \displaystyle v_{sd}^{s’} = v_{sd}^s-p_d^s = r_si_{sd}^s + \sigma l_s\frac{di_{sd}^s}{dt} $
$ \displaystyle v_{sq}^{s’} = v_{sq}^s-p_q^s = r_si_{sq}^s + \sigma l_s\frac{di_{sq}^s}{dt} $
Usando a transformada de Laplace
$ \displaystyle v_{sd}^{s’}(s) = r_sI_{sd}^s(s)+\sigma l_s s I_{sd}^s(s) $
$ \displaystyle \frac{I_{sd}^s(s)}{V_{sd}^{s’}(s)} = \frac{1}{\sigma l_s s + r_s} = \frac{1/\sigma l_s}{s + r_s /\sigma l_s } $
$ \displaystyle v_{sq}^{s’}(s) = r_sI_{sq}^s(s)+\sigma l_s s I_{sq}^s(s) $
$ \displaystyle \frac{I_{sq}^s(s)}{V_{sq}^{s’}(s)} = \frac{1}{\sigma l_s s + r_s} = \frac{1/\sigma l_s}{s + r_s /\sigma l_s } $
Para o sistema de primeira ordem temos
$ \displaystyle k = \frac{1}{\sigma l_s} $
$ \displaystyle \tau = \frac{\sigma l_s}{r_s} $
onde,
$ \displaystyle 0<\sigma<1 $

Para um PMSM com $ r_s = 4.3 \omega $ e $ l_s = 0.067H $ e $ \sigma = 0.5 $
$ \displaystyle k = \frac{1}{0,5 \times 0,067} = 29,850746269 $
$ \displaystyle \tau = \frac{0.5 \times 0,067}{4.3} = 0,007790698 \,\,\, $
Referências
- Notas de aula do prof. dr. Caio Dorneles Cunha e prof. dr. Thiago de Oliveira Alves Rocha.
- Mohan, Undeland e Robbins, Power Electronics. Willey, 1989.
- W. Leonard, Control of Electrical Drives. Springer, 2001 2Ed.
- M. E. El-Hawary, Modeling and High Performance Control of Electric Machines. John Wiley & Sons, 2005.
- Chen-Mun Ong, Dynamic Simulation of Electric Machinery. Prentice-Hall, 1997.
- R. Krishnan, Eletric Motor Drives, Modeling, Analysis, and Control. Prentice-Hall, 2001.
- Ned Mohan, Máquinas Elétricas e Acionamentos. LTC, 2015.
- Ivo Barbi, Teoria Fundamental do Motor de Indução. Editora da UFSC/ELETROBRÁS, 1985.
