
Os valores por unidade (p.u) correspondem a uma mudança de escala nas grandezas principais de Sistemas Elétricos de Potência (SEPs), tais como: tensão, corrente, impedância e potência.
Vantagens
- melhor visão da análise elétrica de sistemas, com vários níveis de tensão distintos;
- resultados numéricos superiores, com parâmetros de rede na mesma ordem de grandeza;
- simplificação no cálculo de circuitos com vários transformadores, pois os valores de tensão, corrente, impedância e potência do transformador em p.u são os mesmos, não importando se estão referidos ao lado primário (alta) ou secundário (baixa).
Valores em p.u para os SEPs monofásicos
Normalmente, definimos a tensão base $ (V_{base}) $ e a potência base $ (S_{base}) $, e depois calculamos as demais grandezas.
| Tensão |
| $ \displaystyle \dot{V}_{p.u} = \frac{\dot{V}}{\dot{V}_{base}} $ |
| Corrente |
| $ \displaystyle \dot{I}_{p.u} = \frac{\dot{I}}{\dot{I}_{base}} = \dot{I} \cdot \left( \frac{V_{base}}{S_{base}} \right) \quad $ ou $ \quad \dot{I}_{p.u} = \frac{S_{p.u}}{V_{p.u}} \qquad\qquad\qquad $ |
| Impedância |
| $ \displaystyle \vec{Z}_{p.u} = \frac{\vec{Z}}{Z_{base}} = \vec{Z} \cdot \left( \frac{I_{base}}{V_{base} } \right) = \vec{Z} \cdot \left( \frac{S_{base}}{V_{base}^2 } \right) $ |
| Resistência |
| $ \displaystyle R_{p.u} = \frac{R}{Z_{base}} = R \cdot \left( \frac{S_{base}}{V_{base}^2 } \right) $ |
| Reatância |
| $ \displaystyle Q_{p.u} = \frac{Q}{Z_{base}} = Q \cdot \left( \frac{S_{base}}{V_{base}^2 } \right) $ |
| Potência aparente |
| $ \displaystyle \dot{S}_{p.u} = \frac{\dot{S}}{S_{base}} $ |
| Potência ativa |
| $ \displaystyle \dot{P}_{p.u} = \frac{\dot{P}}{S_{base}} $ |
| Potência reativa |
| $ \displaystyle \dot{Q}_{p.u} = \frac{\dot{Q}}{S_{base}} $ |
Valores em p.u para os SEPs trifásicos
Normalmente, definimos a potência trifásica base $ (S_{{3 \phi}_{base}}) $ e a tensão de linha base $ (V_{L_{base}}) $ e depois calculamos as demais grandezas.
| Tensão |
| $ \displaystyle \dot{V}_{F_{p.u}} = \frac{\dot{V}}{V_{F_{p.u}}} = \frac{\dot{V}}{\frac{V_{L_{base}}}{\sqrt{3}} } = \dot{V} \cdot \left( \frac{\sqrt{3}}{V_{L_{base}}} \right) $ $ \dot{V}_{L_{p.u}} = \frac{\dot{V}}{V_{L_{base}}} \qquad\qquad\qquad\qquad\quad\,\,\,\, $ |
| Corrente |
| $ \displaystyle \dot{I}_{F_{p.u}} = \dot{I}_{L_{p.u}} = \frac{\dot{I}}{\dot{I}_{L_{base}}} = \frac{\dot{I}}{ \frac{S_{{3 \phi}_{base}}}{\sqrt{3} \cdot V_{L_{base}}} } = \dot{I} \cdot \left( \sqrt{3} \cdot \frac{V_{L_{base}}}{S_{{3 \phi}_{base}}} \right) \quad $ ou $ \quad \dot{I}_{F_{p.u}} = \frac{S_{p.u}}{\sqrt{3} \cdot V_{p.u}} \qquad\qquad\qquad\qquad\qquad\,\,\,\, $ |
| Impedância |
| $ \displaystyle \vec{Z}_{p.u} = \frac{\vec{Z}}{Z_{base}} = \frac{\vec{Z}}{\frac{ V_{L_{base}}}{ \sqrt{3} \cdot I_{L_{base}}}} = \frac{\vec{Z}}{\frac{ V_{L_{base}}^2}{S_{{3 \phi}_{base}}}} = \vec{Z} \cdot \left( \frac{S_{{3 \phi}_{base}}}{V_{L_{base}}^2 } \right) $ |
| Resistência |
| $ \displaystyle R_{p.u} = \frac{R}{Z_{base}} = R \cdot \left( \frac{S_{{3 \phi}_{base}}}{V_{base}^2 } \right) $ |
| Reatância |
| $ \displaystyle Q_{p.u} = \frac{Q}{Z_{base}} = Q \cdot \left( \frac{S_{{3 \phi}_{base}}}{V_{base}^2 } \right) $ |
| Potência aparente |
| $ \displaystyle \dot{S}_{p.u} = \frac{\dot{S}}{S_{{3 \phi}_{base}}} $ |
| Potência ativa |
| $ \displaystyle \dot{P}_{p.u} = \frac{\dot{P}}{S_{{3 \phi}_{base}}} $ |
| Potência reativa |
| $ \displaystyle \dot{Q}_{p.u} = \frac{\dot{Q}}{S_{{3 \phi}_{base}}} $ |
Aplicação em redes complexas
Numa rede complexa, o procedimento a seguir para a definição das fases será o seguinte:
- Definir a base de potência $ S_b $ para todo o sistema;
- Identificar as diferentes zonas de tensão;
- Definir a base de tensão composta $ V_{b1} $ para uma das zonas de tensão (designada arbitrariamente por zona 1);
- Em cada zona $ k $ ainda sem base definida, que esteja ligada a uma zona com base $ V_{bi} $ através de um transformador com razão de transformação (Tap) $ V_i/V_k $ definir como base a tensão $ V_{bk} = (V_k/V_i).V_{bi} $;
- Calcular as bases de impedância e de corrente para cada zona a partir das bases de potência e de tensão.
Mudança de base
Nos SEPs, os valores das características dos elementos de rede são fornecidos em valores p.u, tendo por base as grandezas nominais dos equipamentos fornecidos pelos fabricantes, ou seja, para uma rede elétrica com diversos níveis de tensões, as tensões bases dependem das relações detensão dos transformadores. Desta forma, cada sub-rede terá umatensão base, mas que dependerá da relação de tensão dos transformadores que interligam esta sub-rede às demais sub-redes. Logo, a pluralidade desses equipamentos nos SEPs exige a execução de mudanças de bases cujo o propósito é padronizar os cálculos em p.u. Entretanto, a potência base $ S_{{3 \phi}_{base}}$ será a mesma para todos os SEPs interligados.

Mudança de base para as características de um SEP
| Tensão |
| $ \displaystyle \dot{V}_{{p.u}_1} = \dot{V}_{{p.u}_2} \cdot \left( \frac{V_{base_2}}{V_{base_1}} \right) $ |
| Corrente |
| $ \displaystyle \dot{I}_{{p.u}_1} = \dot{I}_{{p.u}_2} \cdot \left( \frac{V_{base_1}}{V_{base_2}} \right) \cdot \left( \frac{S_{base_2}}{S_{base_1}} \right) $ |
| Impedância |
| $ \displaystyle \vec{Z}_{p.u_1} = \vec{Z}_{p.u_2} \cdot { \left( \frac{V_{base_2}}{V_{base_1}} \right) }^2 \cdot \left( \frac{S_{base_1}}{S_{base_2}} \right) $ |
Os fabricantes fornecem apenas um valor em p.u para a impedância dos transformadores pois o valor referido ao lado de alta tensão é igual ao valor referido ao lado de baixa tensão.
Fonte: https://www.weg.net/catalog/weg/BR/pt/Gera%C3%A7%C3%A3o%2C-Transmiss%C3%A3o-e-Distribui%C3%A7%C3%A3o/Transformadores-a-Seco/c/GTD_TS
Isso ocorre quando as tensões de base $ ( V_{base} ) $ são os valores nominais de alta $ ( V_{N_{AT}} ) $ e baixa tensão $ ( V_{N_{BT}} ) $, a potência base $ ( S_{base} $ ou $ S_{{3 \phi}_{base}} ) $ seja a nominal do transformador $ ( S_N $ ou $ S_{{3\phi}_N} ) $ e a relação de transformação não seja alterada. Portanto, podemos representar a impedância de um transformador referida ao lado de alta ou baixa tensão, dá na mesma!
$ \displaystyle \vec{Z}_{p.u_{BT}}=\vec{Z}_{p.u_{AT}}\cdot\left( \frac{V_{base_{BT}}}{V_{base_{AT}}} \right)^2=\vec{Z}_{p.u_{AT}} \cdot \left( \frac{N_{base_{BT}}}{N_{base_{AT}}} \right)^2 $
$ \displaystyle \vec{Z}_{p.u_{AT}}=\vec{Z}_{p.u_{BT}}\cdot\left( \frac{V_{base_{AT}}}{V_{base_{BT}}} \right)^2=\vec{Z}_{p.u_{BT}} \cdot \left( \frac{N_{base_{AT}}}{N_{base_{BT}}} \right)^2 $
$ \displaystyle \vec{Z}_{p.u_{BT}}=\vec{Z}_{p.u_{AT}} $
Logo, fica provado que a impedância em p.u do transformador tem valor único, qualquer que seja o lado referido, ou seja, o transformador passa a se comportar como se tivesse relação de espiras igual a 1, o que significa que o transformado passa a ser representado como uma carga singular no circuito do SEP.
| Potência |
| $ \displaystyle \dot{S}_{p.u_1}=\dot{S}_{p.u_2} \cdot \left( \frac{S_{base_2}}{S_{base_1}} \right) $ |
Exemplo
Qual é a impedância $ Z_{ab} $ no circuito abaixo?
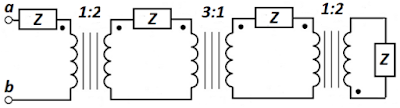
$ \displaystyle \vec{Z}_{p.u_3}=\vec{Z}_{p.u} \cdot \left[ 1+ {\left( \frac{1}{2} \right)}^2 \right] = 1,250 \cdot \vec{Z}_{p.u} \qquad\qquad\qquad\,\,\,\,\, $
$ \displaystyle \vec{Z}_{p.u_2}=\vec{Z}_{p.u} \cdot \left[ 1+ {\left( \frac{3}{1} \right)}^2 \cdot 1,25 \right] = 1,225\times10^1 \cdot \vec{Z}_{p.u} \quad $
$ \displaystyle \vec{Z}_{p.u_{ab}}=\vec{Z}_{p.u} \cdot \left[ 1+ {\left( \frac{1}{2} \right)}^2 \cdot 1,225\times10^1 \right] = 4,063 \cdot \vec{Z}_{p.u} $
Referências
- Notas de aula do prof. Dr. Max Chianca Pimentel Filho.
- MONTICELLI, Alcir. Introdução a Sistemas de Energia Elétrica, UNICAMP, 2Ed, São Paulo-SP, 2011.
- ELGERD, O. I., Introdução à Teoria de Sistemas de Energia Elétrica, McGraw-Hill, São Paulo-SP, 1981.
- J. J. Grainger and W.D. Stevenson Jr. Power Systems Analysis. McGraw-Hill, 1994.
- J. D. Glover, M. S. Sarma and T. J. Overbye. Power Systems Analysis and Design, 4th Edition. Thomson, 2008.
- A. R. Bergen and V. Vittal. Power Systems Analysis, 2nd Edition. Prentice Hall, 2000.
- Prabha Kundur. Power System Stability and Control. McGraw-Hill, 1994.
- GÓMEZ-EXPÓSITO, A., CONJETO, A. J., CAÑIZARES, C., Sistemas de Energia Elétrica – Análise e Operação, LTC, Rio de Janeiro, 2011.
