A maior parte do sistema interligado nacional (SIN) tem a configuração trifásica, que permite o transporte de potência de forma eficiente e com qualidade. Porém, em alguns casos se utiliza a configuração bifásica ou monofásica com retorno pela terra. Geralmente, em pequenas comunidades rurais ou consumidores isolados estes sistemas são utilizado por serem de menor custo. As configurações trifásicas são utilizadas para o acionamento de máquinas elétricas, união de redes de transmissão/distribuição, alimentação de pequenos/médios e grandes consumidores, conexão de diversos tipos de usinas geradoras dentre outros n-ésimos sistemas trifásicos (Figura 01).
Figura 01 – Conexão trifásica de um transformador à rede de alta tensão para alimentação de uma rede de baixa tensão.
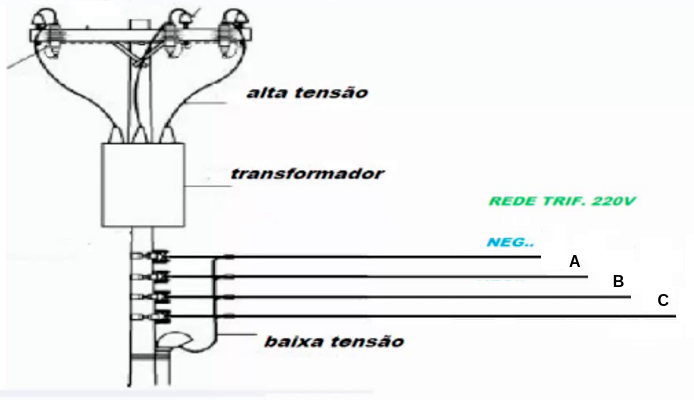
Fonte: Autor.
Ligações Trifásicas ( $Y$ e $ \triangle $ )
Nos sistemas trifásicos, tanto as fontes trifásica (geradores) quanto as cargas trifásica (transformadores, unidades consumidoras, máquinas elétricas) podem estar conectadas em estrela ou em triângulo. Neste cenário, existem dois tipos de ligações ( $Y$ e $ \triangle $ ) e consequentemente diversos tipos de configurações trifásicas e representações fatoriais.
A ligação estrela $Y$ nas configurações trifásicas devido a presença do fio de retorno em seu arranjo que possibilita a identificação de desequilíbrio, e por sua observação ocorrências de curto-circuito.
Escolha de Referencial
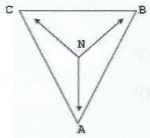
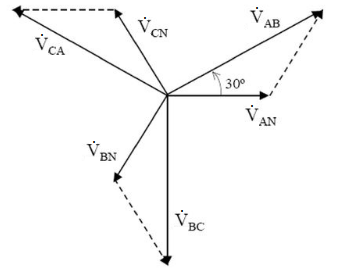
A escolha de uma tensão de referência com ângulos de fase nulo determina os ângulos de fase de todas as demais tensões do sistema, ou seja, a ordem cronológica ao qual as tensões atingem seus valores de pico e, consequentemente, sua representação fasorial. No exemplo a seguir $V_{AB}$ foi escolhida para referência. O triângulo abaixo mostra todas as tensões.
| Sequência ABC ou Sequência Direta ou Sequência Positiva | Sequência ACB ou Sequência Inversa ou Sequência Negativa |
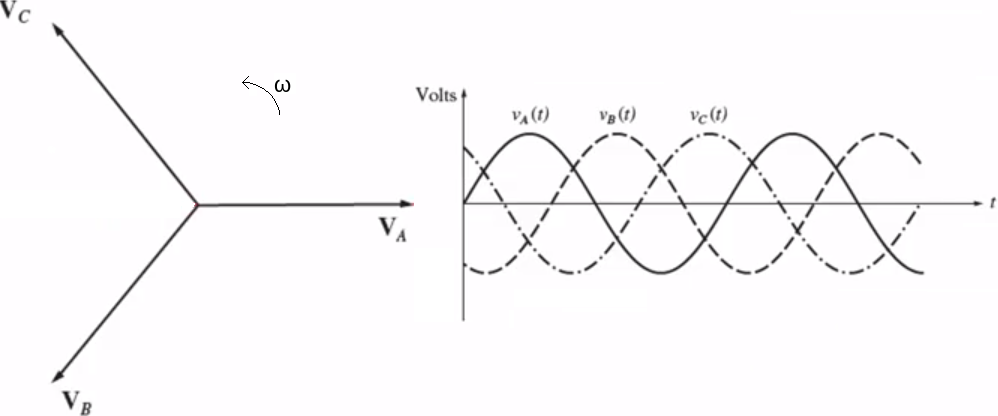 | 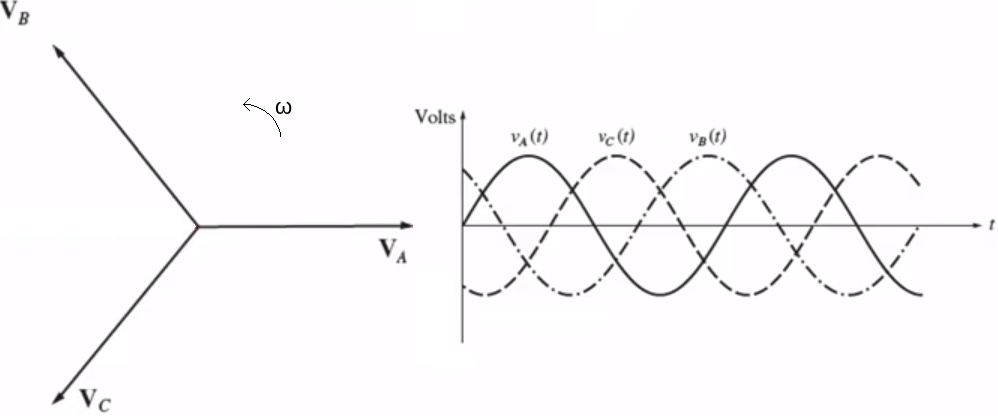 |
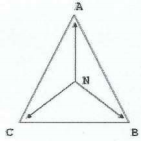 |  |
| $ \begin{cases} \dot{V}_{AB} = V \angle 0^\circ \\ \dot{V}_{BC} = V \angle -120^\circ \\ \dot{V}_{CA} = V \angle +120^\circ \end{cases} $ | $ \begin{cases} \dot{V}_{AB} = V \angle 0^\circ \\ \dot{V}_{BC} = V \angle +120^\circ \\ \dot{V}_{CA} = V \angle -120^\circ \end{cases} $ |
| $ \begin{cases} \dot{V}_{AN} = \frac{V_L}{\sqrt{3}} \angle -30^\circ \\ \dot{V}_{BN} = \frac{V_L}{\sqrt{3}} \angle -150^\circ \\ \dot{V}_{CN} = \frac{V_L}{\sqrt{3}} \angle +90^\circ \end{cases} $ | $ \begin{cases} \dot{V}_{AN} = \frac{V_L}{\sqrt{3}} \angle +30^\circ \\ \dot{V}_{BN} = \frac{V_L}{\sqrt{3}} \angle +150^\circ \\ \dot{V}_{CN} = \frac{V_L}{\sqrt{3}} \angle -90^\circ \end{cases} $ |
Estrela ou $ Y $
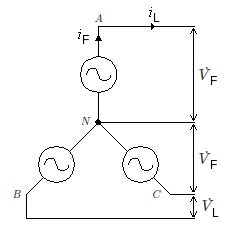
Pela 1ª Lei de Kirchhoff e independente da sequência de fases, as correntes de linha e de fase tem a seguinte relação
$ \dot{I}_L=\dot{I}_F $
A relação entre as tensões de linha e de fase para as sequências de fases são
| Sequência Positiva | Sequência Negativa |
| $\dot{V}_L=\sqrt{3}\dot{V}_F\angle+30^\circ$ | $\dot{V}_L=\sqrt{3}\dot{V}_F\angle-30^\circ$ |
Delta ou $ \triangle $

Pela 2ª Lei de Kirchhoff e independente da sequência de fase, as tensões de linha e de fase tem a seguinte relação
$ \dot{V}_L=\dot{V}_F $
A relação entre as correntes de linhas e de fase para as sequências de fases são
| Sequência Positiva | Sequência Negativa |
| $\dot{I}_L=\sqrt{3}\dot{I}_F\angle-30^\circ$ | $\dot{I}_L=\sqrt{3}\dot{I}_F\angle+30^\circ$ |
Uma carga ligada $\triangle$ consome 3 vezes mais potência que a mesma carga ligada em $Y$, cuja uma das consequências é o conceito da partida $Y-\triangle$ do Motor de Indução.
Modos de operação
As duas ligações de fontes geradoras ( $Y$ e $ \triangle $ ) podem estar conectadas a diversos sistemas trifásicos que poderão operar equilibrado (carga equilibrada, mesma impedância nas três fases), tais como os motores elétricos e outros dispositivos projetados, ou operar desequilibrado (carga desequilibrada, diferentes impedâncias nas três fases e corrente de neutro), tais como os transformadores de distribuição de energia elétrica cuja as cargas (unidades consumidoras) possuem diferentes valores ao longo do dia.
Configuração $ Y-Y $
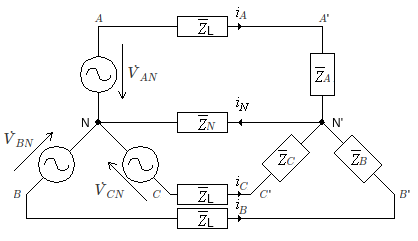
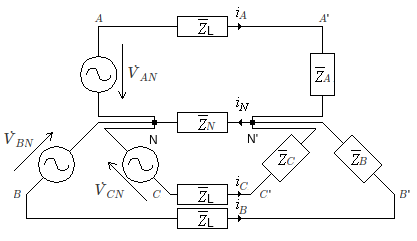
Pela 2ª Lei de Kirchhoff as tensões de fase no gerador são
$
V_{F_G}
=
\begin{cases}
\dot{V}_{AN}=(\vec{Z}_A+\vec{Z}_L) \cdot I_A+\vec{Z}_{N} \cdot \dot{I}_N \\
\dot{V}_{BN}=(\vec{Z}_B+\vec{Z}_L) \cdot I_B+\vec{Z}_{N} \cdot \dot{I}_N \\
\dot{V}_{CN}=(\vec{Z}_C+\vec{Z}_L) \cdot I_C+\vec{Z}_{N} \cdot \dot{I}_N
\end{cases}
$
Isolando as correntes temos
$
I
=
\begin{cases}
\dot{I}_A=\frac{\dot{V}_{AN}}{(\vec{Z}_{A}+\vec{Z}_{L})}-\frac{\vec{Z}_{N}}{(\vec{Z}_{A}+\vec{Z}_{L})}\cdot \dot{I}_N \\
\dot{I}_B=\frac{\dot{V}_{BN}}{(\vec{Z}_{B}+\vec{Z}_{L})}-\frac{\vec{Z}_{N}}{(\vec{Z}_{A}+\vec{Z}_{L})}\cdot \dot{I}_N \\
\dot{I}_C=\frac{\dot{V}_{CN}}{(\vec{Z}_{C}+\vec{Z}_{L})}-\frac{\vec{Z}_{N}}{(\vec{Z}_{A}+\vec{Z}_{L})}\cdot \dot{I}_N
\end{cases}
$
Pela lei de Ohm e pela 2ª Lei de Kirchhoff as tensões de fase e linha na carga são, respectivamente
$
V_{F_C}
=
\begin{cases}
\dot{V}_{A’N’}=\vec{Z}_A \cdot \dot{I}_A \\
\dot{V}_{B’N’}=\vec{Z}_B \cdot \dot{I}_B \\
\dot{V}_{C’N’}=\vec{Z}_C \cdot \dot{I}_C
\end{cases}
\qquad
V_{L_C}
=
\begin{cases}
\dot{V}_{A’B’}=\dot{V}_{A’N’}-\dot{V}_{B’N’} \\
\dot{V}_{B’C’}=\dot{V}_{B’N’}-\dot{V}_{C’N’} \\
\dot{V}_{C’A’}=\dot{V}_{C’N’}-\dot{V}_{A’N’}
\end{cases}
$
Pela 1ª e 2ª Lei de Kirchhoff a corrente e as tensões no neutro são, respectivamente
$ \displaystyle \dot{I}_{N}=\dot{I}_{A}+\dot{I}_{B}+\dot{I}_{C}=\frac{\frac{\dot{V}_{AN}}{(\vec{Z}_{A}+\vec{Z}_{L})}+\frac{\dot{V}_{BN}}{(\vec{Z}_{B}+\vec{Z}_{L})}+\frac{\dot{V}_{CN}}{(\vec{Z}_{C}+\vec{Z}_{L})}}{1+\frac{\vec{Z}_{N}}{(\vec{Z}_{A}+\vec{Z}_{L})}+\frac{\vec{Z}_{N}}{(\vec{Z}_{B}+\vec{Z}_{L})}+\frac{\vec{Z}_{N}}{(\vec{Z}_{C}+\vec{Z}_{L})}} $
$ \displaystyle \dot{V}_{NN’}=-\vec{Z}_N\cdot\dot{I}_{N} \qquad \dot{V}_{N’N}=\vec{Z}_N\cdot\dot{I}_{N} $
$ \displaystyle \dot{I}_{N}= -( \dot{I}_{A} + \dot{I}_{B} + \dot{I}_{C} ) = 0 $
Exemplo
1. Considere uma fonte trifásica equilibrada, ligada em estrela aterrada, alimentando uma carga trifásica desequilibrada, ligada em estrela isolada. As correntes nas fases “A” e “B” são: $ \dot{I}_{A}=j5 \, A $ e $ \dot{I}_{B} = 10 \angle -30^{\circ} \, A $, então, pela 1ª Lei de Kirchhoff, a corrente na fase “C”, $ \dot{I}_{C} $, é
$ \dot{I}_{C} = -\dot{I}_{A}-\dot{I}_{B} = -8,66 A $
2. Observe a conexão trifásica abaixo,
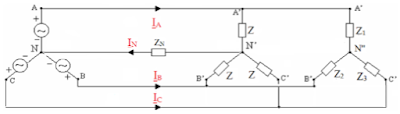
Nesse sistema, os fasores que representam as tensões na fonte são: $ \dot{V}_{AN}=V \angle 0^{\circ} $, $ \dot{V}_{BN}=V \angle -120^{\circ} $ e $ \dot{V}_{CN}=V \angle 120^{\circ} $. A carga 1 é trifásica e apresenta a impedância $ \bar{Z} = Z \angle \theta $. Já a carga 2, também trifásica, é dotada das impedâncias $ \bar{Z}_{1} = Z_{1} \angle \theta_{1} $, $ \bar{Z}_{1} = Z_{2} \angle \theta_{2} $ e $ \bar{Z}_{3} = Z_{3} \angle \theta_{3} $. Por fim, há um fio neutro cuja impedância é $ \bar{Z}_{N} = Z_{N} \angle \theta_{N} $. Observe as afirmativas:
I- O sistema possui sequência de fases ABC, é simétrico e equilibrado;
Não, pois apresenta carga desequilibrada.
II- A corrente \( \dot{I}_{N} \) no fio neutro é nula;
Pela 1ª Lei de Kirchhoff, a corrente no neutro é calculada por,
$ \dot{I}_{N}= ( \dot{I}_{A’} + \dot{I}_{B’} + \dot{I}_{C’} ) = 0 $
III- $ V_{F_{S}} = V_{F_{carga1}} $
Sim, pois a carga 1 é equilibrada.
IV- Uma vez conhecidas as tensões de fase na carga 2, para calcular a tensão de linha $ \dot{V}_{A’B’} $, nesta mesma carga, basta usar a equação $ \dot{V}_{A’B’} = \sqrt{3} . V_{A’N”} \angle 30^{\circ} $.
Não, as tensões de linha são diferentes pois a carga 2 é desequilibrada.
Configuração $ \triangle -Y $
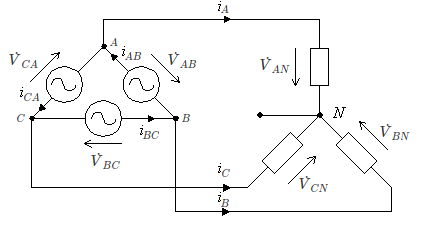
Pela 2ª Lei de Kirchhoff,
$ -\dot{V}_{AB}+\vec{Z}_A\dot{I}_A-\vec{Z}_B\dot{I}_B=0 $
Para uma carga equilibrada $ ( \vec{Z}_A=\vec{Z}_B=\vec{Z}_C=\vec{Z}_Y ) $
$ \dot{I}A-\dot{I}_B=\frac{\dot{V}{AB}}{\vec{Z}} $
Configuração $ Y-\triangle $
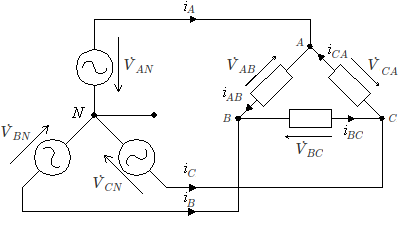
Pela 2ª Lei de Kirchhoff as correntes na carga são
$
I_{F}
=
\begin{cases}
\dot{I}_{AB}=\frac{\dot{V}_{AN}-\dot{V}_{BN}}{\vec{Z}_A}=\frac{\dot{V}_{AB}}{\vec{Z}_A} \\
\dot{I}_{BC}=\frac{\dot{V}_{BN}-\dot{V}_{CN}}{\vec{Z}_B}=\frac{\dot{V}_{BC}}{\vec{Z}_B} \\
\dot{I}_{CA}=\frac{\dot{V}_{CN}-\dot{V}_{AN}}{\vec{Z}_C}=\frac{\dot{V}_{CA}}{\vec{Z}_C}
\end{cases}
$
As correntes de linha são determinadas com a aplicação da 1ª lei de kirchhoff em cada nó da fonte
$
I_{L}
=
\begin{cases}
\dot{I}_{A}\,=\, \dot{I}_{AB}-\dot{I}_{CA} \\
\dot{I}_{B}\,=\, \dot{I}_{BC}-\dot{I}_{AB} \\
\dot{I}_{C}\,=\, \dot{I}_{CA}-\dot{I}_{BC}
\end{cases}
$
onde,
$ \dot{I}L = \sqrt{3} \,\,. I_F\angle(\theta{F}-30^{\circ}) $
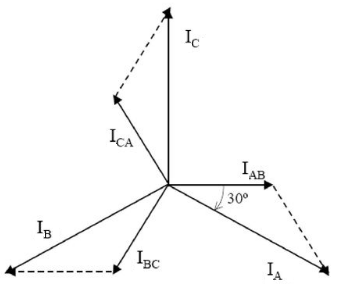
Neste tipo de configuração o fio neutro fica desligado $ ( \dot{I}_{N} = 0 ) $.
Configuração $ \triangle $ – $ \triangle $
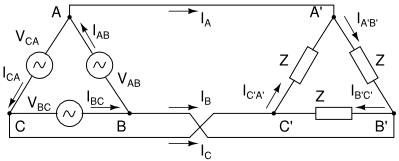
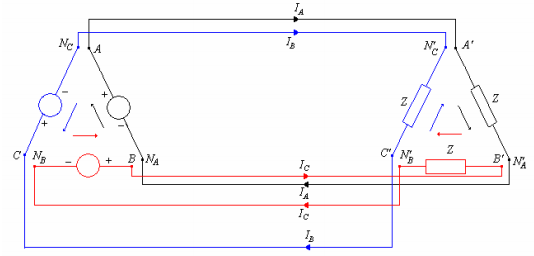
Configuração $ \triangle-\triangle $ (a) Gerador em $ \triangle $ e Carga em $ \triangle $. (b) Representação monofásica.
Pela lei de Ohm as correntes de fase na carga são
$
I_{F}
=
\begin{cases}
\dot{I}_{A’B’}=\frac{\dot{V}_{AB}}{\vec{Z}_A} \\
\dot{I}_{B’C’}=\frac{\dot{V}_{BC}}{\vec{Z}_B} \\
\dot{I}_{C’A’}=\frac{\dot{V}_{CA}}{\vec{Z}_C}
\end{cases}
\qquad
$
Pela 1ª Lei de Kirchhoff as correntes de linha são
$
I_{L}
=
\begin{cases}
\dot{I}_{A}=\dot{I}_{A’B’}-\dot{I}_{C’A’} \\
\dot{I}_{B}=\dot{I}_{B’C’}-\dot{I}_{A’B’} \\
\dot{I}_{C}=\dot{I}_{C’A’}-\dot{I}_{B’C’}
\end{cases}
$
onde,
$ \dot{I}L = \sqrt{3} \,\,. I_F\angle(\theta{F}-30^{\circ}) $
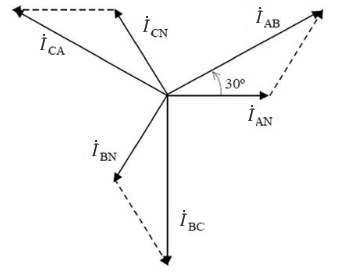
Neste tipo de configuração o fio neutro fica desligado $ ( \dot{I}_{N} = 0 ) $.
Conversão de carga Estrela Triângulo
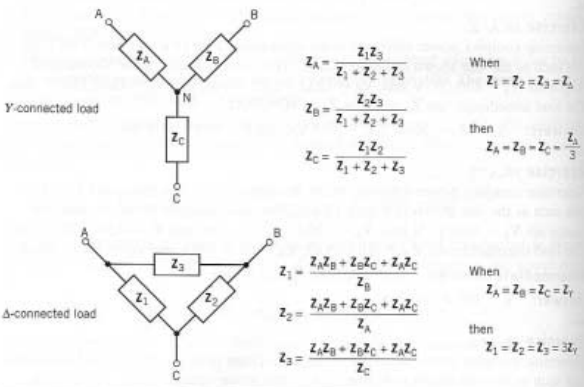
Resumo das conexões de carga

Conexões dos transformadores trifásicos
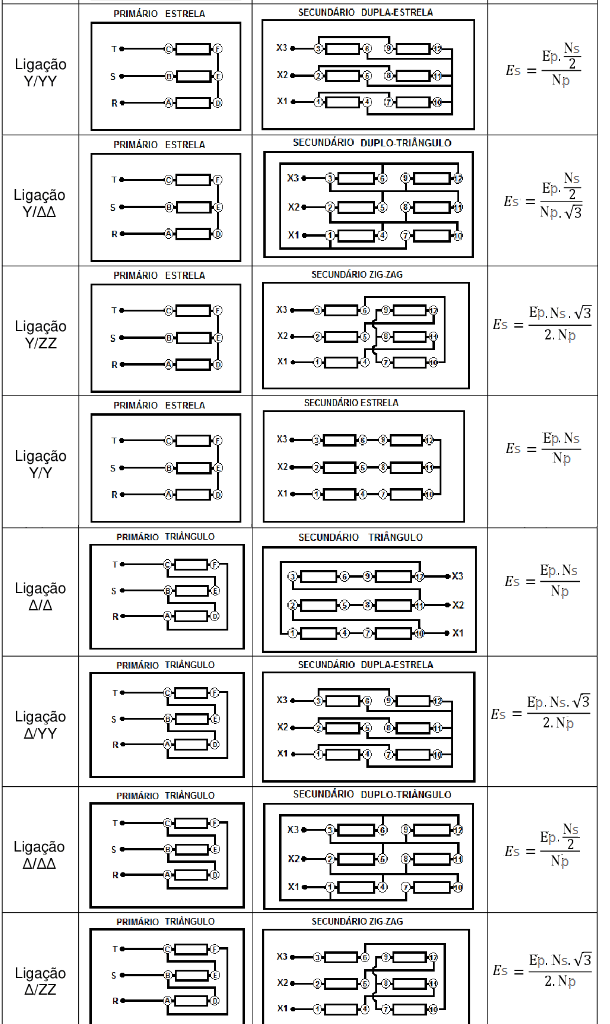
Exemplo
1. De acordo com a figura ao lado, uma planta industrial a ser inaugurada tem quatro cargas elétricas que devem ser conectadas a uma rede de distribuição de baixa tensão trifásica. As cargas são as seguintes:
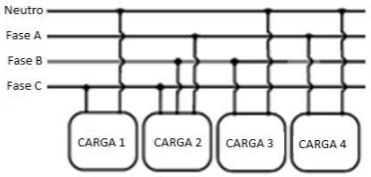
- Carga 1: Aparelho de ar condicionado monofásico com potência $1540 $ VA e fator de potência $ 0,5 $ indutivo;
- Carga 2: Motor elétrico trifásico com potência reativa de $ 3600 $ VAr e fator de potência $ 0,8 $ indutivo;
- Carga 3: Ventilador industrial monofásico com impedância $ Z = 22 \angle 30^{\circ} \, \Omega $;
- Carga 4: Forno elétrico resistivo monofásico com potência de $ 2200 $ VA.
Considere que o sistema é simétrico, com sequência de fases $ ABC $. Tomando como fasor de referência a tensão $ \dot{V}_{AN} \, = 220 \angle 40^{\circ} \, V $, analise as afirmações a seguir:
I- Em cada uma das fases, a potência ativa solicitada pelo motor é $ 1600 \, W$;
II- Acorrente solicitada pelo aparelho ar-condicionado é $ \dot{I}_{C} = 7,0 \angle 100^{\circ} \, A $;
III- A potência reativa solicitada pelo ventilador é $ 1100 $ VAr.
Referências
- OLIVEIRA, C. C. B; SCHIMDT, H. P.; KAGAN, N; ROBBA, E. J. Introdução aos Sistemas Elétricos de Potência – Componentes Simétricas. São Paulo: Blucher, 2000.
- MONTICELLI, A.; GARCIA, A. Introdução a Sistemas de Energia Elétrica. São Paulo: Unicamp, 2003.
- BOYLESTAD, R. L. Introdução à Análise de Circuitos. São Paulo: Pearson, 2004.
