Podendo ser considerado como uma contribuição ao método de Gauss, o método de Gauss-Seidel é um método iterativo para resolução de sistemas de equações lineares com $ n $ variáveis desconhecidas. O seu nome é uma homenagem aos matemáticos Carl Friedrich Gauss (1777-1855) e Philipp Ludwig von Seidel (1821-1896), Figura 01.
Figura 01 – Matemáticos Carl Friedrich Gauss e Philipp Ludwig von Seidel.

Fonte: Autor.
Seidel ao estudar o método de Gauss para a resolução de equações lineares observou que, substituindo o valor anterior pelo valor calculado apenas no final da iteração o sistema convergiria mais rapidamente. Desta forma, concluiu que o número de iterações para obtenção da solução passa a ser menor ao adotar essa estratégia.
Para ilustração, consideremos o sistema de equações lineares de duas variáveis ($x$ e $y$) abaixo:
| \begin{matrix} y-3x+1,9=0 \\ y+x^2-1,8=0 \end{matrix} | (1) |
Em seguida, apresenta-se a solução do sistema (Figura 2) pelo método de Gauss e o método de Gauss-Seidel.
Figura 02 – Gráfico da solução do sistema de equações lineares (1).
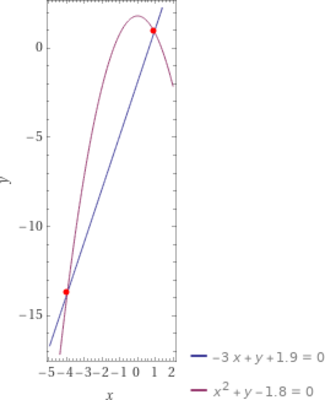
Fonte: https://www.wolframalpha.com/
Método de Gauss
Pelo método de Gauss reescreve-se as equações em (1) como:
| \begin{matrix} \quad\, x=\dfrac{y}{3}+0,633 \\ \, y=1,8-x^2 \end{matrix} | (2) |
Arbitrando como valores iniciais $ x^{(0)}=y^{(0)}=1 $ e substituindo em x e y no lado direito das equações em (2):
| \begin{matrix} \quad x^{(1)}=\dfrac{y^ {(0)}}{3}+0,633=0,966 \\ \, y^{(1)}=1,8-{(x^{(0)})}^2=0,8 \end{matrix} | (3) |
As sucessivas iterações para x e y podem ser descritas de forma mais geral por:
| \begin{matrix} x^{(i+1)}=\dfrac{y^ {(i)}}{3}+0,633 \\ \, y^{(i+1)}=1,8-{(x^{(i)})}^2 \end{matrix} | (4) |
onde:
- o índice $ ^{(i+1)} $ significa o valor computado na iteração atual;
- o índice $ ^{(i)} $ significa o valor na iteração anterior.
Considerando o critério de parada:
| max $ \left( \left| x^{(i+1)}-x^{(i)} \right| ; \left| y^{(i+1)}-y^{(i)} \right| \right) < $ precisão Número de iterações < Número Máximo de Iterações | (5) |
Adotando-se uma precisão, $ \epsilon $= 1e-6, e um número máximo de iterações, $ N $=1e3, temos que, após 50 iterações, os resultados convergem para valores muito próximos à solução exata:
| $ \begin{matrix} x=0,939057 \\ y=0,918171 \end{matrix} $ | (6) |
OBS.: valores iniciais escolhidos à revelia podem levar à divergência da solução como, por exemplo, para este problema, $ x^{(0)}=y^{(0)}=10 $. Assim, orienta-se ao estudo e compreensão da natureza do problema representado para escolha assertiva de seus valores iniciais.
Método de Gauss-Seidel
- Para computar $ x^{(i+1)} $ do sistema (4) substitui-se a variável $ y^{(i)} $;
- Contudo, para computar $ y^{(i+1)} $ do sistema (4), substitui-se a variável $ x^{(i)} $ por seu valor atual $ x^{(i+1)} $.
Assim, o algoritmo para o método de Gauss-Seidel pode ser escrito como:
00) Entrar com valor inicial para y: $ y^{(0)}=1 $
01) Calcular iteração para $x$:
| $ x^{(i+1)}=\dfrac{y^ {(i)}}{3}+0,633 $ | (7) |
02) Calcular iteração para $y$ com $x$ atual:
| $ y^{(i+1)}=1,8-{(x^{(i+1)})}^2 $ | (8) |
03) Atualiza $y$:
| $ y^{(i)}=y^{(i+1)} $ | (9) |
04) Executa-se iterativamente os processos de 01 ao 03 até o critério de parada (5) ser alcançado.
Nesse caso, novamente com a precisão, $ \epsilon $= 1e-6, e um número máximo de iterações, $ N $=1e3, temos que, após 27 iterações, os resultados convergem para valores muito próximos à solução exata obtida em (6). Reduzindo-se em incríveis 46% o número de iterações necessárias para convergência neste problema.
Referências
- J. J. Grainger and W.D. Stevenson Jr. Power Systems Analysis. McGraw-Hill, 1994.
- J. D. Glover, M. S. Sarma and T. J. Overbye. Power Systems Analysis and Design, 4th Edition, Thomson, 2008.
- A. R. Bergen and V. Vitta. Power Systems Analysis, 2nd Edition, Prentice Hall, 2000.
- Prabha Kundur. Power System Stability and Control. McGraw-Hill, 1994.
- GÓMEZ-EXPÓSITO, A., CONJETO, A. J., CAÑIZARES, C., Sistemas de Energia Elétrica – Análise e Operação, LTC, Rio de Janeiro, 2011.
