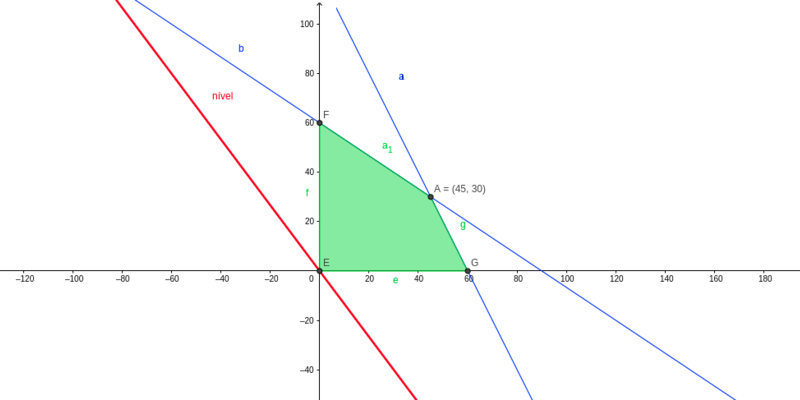
Fonte: GeoGebra
Em computação, Programação Linear (PL) são problemas de otimização combinatória nos quais a função objetivo e as restrições são todas lineares.
Geometricamente, as restrições lineares definem um poliedro convexo, que é chamado de conjunto dos pontos viáveis ou região de factibilidade.
A função objetivo ser linear implica que uma solução ótima pode ocorrer apenas em um ponto da fronteira do conjunto de pontos viáveis. Também, sendo a função objetivo linear, observa-se que todo ótimo local é automaticamente um ótimo global.
Existem duas situações nas quais uma solução ótima não pode ser encontrada:
1. Se as restrições se contradizem. Logo, a região factível é vazia e não pode haver solução ótima, e o problema é dito inviável, por exemplo:
| função objetivo | restrições |
|---|---|
| $ \displaystyle z=x$ |
$ x \geqslant 2 $ e $ x\leqslant 1 $ |
2. Quando o poliedro pode ser ilimitado na direção da função objetivo, neste caso não existe solução ótima uma vez que as soluções arbitrariamente grandes da função objetivo podem ser construídas, e o problema é dito ilimitado, por exemplo:
| função objetivo | restrições |
|---|---|
| $ \displaystyle z=x_1+3x_2$ | $ x_1,\, x_2 \geqslant 0 $ $ x_1 + x_2 \geqslant 10 $ |
Estas condições são frequentemente eliminadas por limitações dos recursos inerentes ao problema que está sendo modelado. Fora estas duas condições irregulares, o ótimo é sempre alcançado num vértice do poliedro. Entretanto, o ótimo nem sempre é único: é possível ter um conjunto de soluções ótimas cobrindo uma aresta ou face do poliedro, ou até mesmo o poliedro todo. Esta última situação pode ocorrer se a função objetivo for uniformemente igual a uma constante.
Alguns problemas de programação linear são apresentados abaixo.
O Problema de Perdas em Redes Elétricas
Em engenharia elétrica, o Problema de Fluxo de Carga é o estudo de sistemas elétricos de potência em regime permanente para uma condição de carga e de geração. A sua solução determina os valores de tensão em todas as $n$ barras do sistema. Com as tensões nas barras e os parâmetros elétricos do sistema pode-se obter as correntes nas linhas e as perdas de potência ativa nas linhas de transmissão para uma condição de operação (carga+geração).
Nesse contexto, o problema de perdas em redes elétricas consiste em minimizar a função objetivo “Perdas” definindo o nível ótimo de potência ativa em cada unidade geradora da rede elétrica para se obter a menor soma de perdas de potência ativa nas $N_{LTs}$ linhas de transmissão.
Sejam:
- $i=1,\,2,\,3,\,\cdots,\,n$ as barras do sistema;
- $j=1,\,2,\,3,\,\cdots,\,n_{LTs}$ as linhas de transmissão;
- $ P_{C_{i}} $ a potência ativa consumida em cada barra;
- $ P_{L_{j}} $ a potência ativa perdida em cada linha de transmissão;
- $ P_{G_{i}} $ a potência ativa gerada em cada barra.
E supondo um sistema com $n$ geradores após o fluxo de carga convergido. A soma da potência ativa gerada em cada gerador deverá ser igual a soma das potências ativas consumidas em cada uma das barras do sistema mais as perdas de potência ativa nas linhas de transmissão:
| $ \displaystyle \sum_{i=1}^{n}P_{C_{i}}+\sum_{j=1}^{n_{LTs}}P_{L_{j}}-\sum_{i=1}^{n}P_{G_{i}}=0 $ | (1) |
Caso se modifique a geração em cada unidade geradora $ (P_{G_{i}}) $, porém conservando a mesma carga consumida $ (P_{C_{i}}) $, o sistema passará a operar em um novo ponto de operação. Considerando as perdas ativas totais $(P_{L})$ como a função objetivo e o despacho de cada unidade geradora como variável de controle:
| $ \displaystyle P_{L}=\sum_{j=1}^{n_{LTs}}P_{L_{j}} $ | (2) |
o problema do fluxo de carga ótimo consistem em determinar o despacho de cada unidade geradora de modo que as perdas sejam mínimas.
Dessa forma, podemos formular o problema de perdas em redes elétricas como:
| função objetivo “Perdas” | restrições |
|---|---|
| $ \displaystyle P_{L}=\sum_{i=1}^{n}P_{G_{i}}-\sum_{i=1}^{n}P_{C_{i}}$ | $ \displaystyle P_{G_{i}} \geqslant 0 $ |
O Problema da Produção Concorrente
Consiste em maximizar o lucro total $(\$)$ ao definir os níveis de produção dos $n$ produtos com os $m$ recursos disponíveis.
Para tal, considere uma unidade fabril com capacidade para produzir $n$ produtos distintos, com diferentes níveis de consumo de recursos e que produzem lucros distintos. Nesse contexto, estes produtos concorrem entre si pelos recursos limitados disponíveis para obtenção do maior lucro possível. Logo, deseja-se definir o nível de produção de cada produto, de forma que o lucro total obtido seja máximo.
Sejam:
- $i=1,\,2,\,3,\,\cdots,\,m\,$: os recursos disponíveis;
- $j=1,\,2,\,3,\,\cdots,\,n\,$: as produtos distintos;
- $x_1,\,x_2,\,x_3,\,\cdots,\,x_n\,$: os níveis de produção dos $n$ produtos;
- $c_1,\,c_2,\,c_3,\,\cdots,\,c_n\,$: os lucros unitários dos $n$ produtos;
- $b_1,\,b_2,\,b_3,\,\cdots,\,b_m\,$: as quantidades dos diferentes recursos disponíveis;
- $a_{i1},\,a_{i2},\,a_{i3},\,\cdots,\,a_{in}\,$: os níveis de consumo do recurso $(i)$ referente a fabricação de uma unidade dos $n$ produtos.
Dessa forma, podemos formular o problema de otimização da produção concorrente como:
| função objetivo “Lucro” | restrições | |
|---|---|---|
| $ \displaystyle z=\sum_{j=1}^{n}c_jx_{j}$ | Estudo de Mercado |
$ \displaystyle \sum_{j=1}^{n}a_{ij}x_j \leqslant b_i $ |
| Numérica | $ \displaystyle x_j \geqslant 0 $ | |
Cujo o propósito é maximizar a função objetivo “Lucro” $(z)$ para se obter os níveis de produção $(x_1,\,x_2,\,x_3,\,\cdots,\,x_n)$ necessários para a obtenção do maior lucro $(z_{max})$.
Exemplo: Uma fábrica produz os produtos I, II e III com níveis de consumo de recursos conforme a tabela seguinte:
| Recursos | Tempo disponível (em horas/mês) |
Horas / unidade dos produtos | ||
|---|---|---|---|---|
| I | II | III | ||
| Máquina 01 | 100 | 2 | 3 | 1 |
| Máquina 02 | 120 | 1 | 1 | 2 |
| Mão de Obra 01 | 176 | 2 | 2 | 3 |
| Mão de Obra 02 | 132 | 1 | 2 | 1 |
| Lucro Unitário ($) | 10 | 15 | 20 | |
| Produção Máxima (unid.) | 80 | 20 | 40 | |
O problema pode ser formulado por:
| função objetivo “Lucro” | restrições | |
|---|---|---|
| $ \displaystyle z=10x_1+15x_2+20x_3 $ | Máquinas | $ \displaystyle 2x_1+3x_2+x_3 \leqslant 100 $ $ \displaystyle x_1+x_2+2x_3 \leqslant 120 $ |
| Mão de Obra | $ \displaystyle 2x_1+2x_2+3x_3 \leqslant 176 $ $ \displaystyle x_1+2x_2+x_3 \leqslant 132 $ |
|
| Mercado | $ \displaystyle x_1 \leqslant 80 ;\quad x_2 \leqslant 20 ;\quad x_3 \leqslant 40 $ | |
| Numérica | $ \displaystyle x_1,\,x_2,\,x_3 \geqslant 0 $ | |
O Problema da Dieta
Consiste em minimizar o custo total $(\$)$ ao definir os níveis de produção de $n$ alimentos com base em uma dieta com o menor consumo vitamínico diário possível.
Para tal, considere que uma pessoa deseja minimizar o custo de sua dieta diária, mantendo os níveis de consumo recomendados para as diferentes vitaminas.
Sejam:
- $i=1,\,2,\,3,\,\cdots,\,m\,$: as vitaminas necessárias;
- $j=1,\,2,\,3,\,\cdots,\,n\,$: os alimentos disponíveis;
- $x_1,\,x_2,\,x_3,\,\cdots,\,x_n\,$: os níveis de produção dos $n$ alimentos pertencentes à dieta;
- $b_1,\,b_2,\,b_3,\,\cdots,\,b_m\,$: os níveis mínimos de consumo da vitamina $i$;
- $a_{i1},\,a_{i2},\,a_{i3},\,\cdots,\,a_{in}\,$: as quantidades da vitamina $(i)$ contidas nos $n$ alimentos disponíveis;
- $c_1,\,c_2,\,c_3,\,\cdots,\,c_n\,$: os custos unitários dos $n$ alimentos disponíveis.
Cujo o propósito é minimizar a função objetivo “Custo” $(C)$ para se obter os níveis de produção dos $n$ alimentos $(x_1,\,x_2,\,x_3,\,\cdots,\,x_n)$, com base em uma dieta com o menor consumo vitamínico diário possível, para a obtenção do menor custo $(C_{min})$.
Exemplo: A dieta de uma pessoa deve constar de 03 alimentos, cujos teores de vitaminas, bem como os níveis mínimos de consumo se encontram na tabela seguinte:
| Vitaminas | Consumo Mínimo diário (mg) |
Teor Vitamínico dos Alimentos (mg / unid) | ||
|---|---|---|---|---|
| $A_1$ | $A_2$ | $A_3$ | ||
| A | 80 | 10 | 5 | 10 |
| B | 70 | 8 | 7 | 6 |
| C | 100 | 1,5 | 3 | 7 |
| D | 60 | 20 | 2 | 9 |
| Preços dos Alimentos ($ / unid) | 80 | 32 | 180 | |
O problema pode ser formulado por:
| função objetivo “Custo” | restrições | |
|---|---|---|
| $ \displaystyle C=80x_1+32x_2+180x_3 $ | Vitaminas | $ \displaystyle 10x_1+5x_2+10x_3 \geqslant 80 $ $ \displaystyle 8x_1+7x_2+6x_3 \geqslant 70 $ $ \displaystyle 15x_1+3x_2+7x_3 \geqslant 100 $ $ \displaystyle 20x_1+2x_2+9x_3 \geqslant 60 $ |
| Numérica | $ \displaystyle x_1,\,x_2,\,x_3 \geqslant 0 $ | |
O Problema de Transporte
Consiste em minimizar o custo total do transporte de mercadorias de $m$ centros fornecedores para $n$ centros consumidores.
Sejam:
- $i=1,\,2,\,3,\,\cdots,\,m\,$: os fornecedores;
- $j=1,\,2,\,3,\,\cdots,\,n\,$: os consumidores;
- $x_{ij}\,$: a quantidade a transportar do fornecedor $(i)$ para o consumidor $(j)$;
- $d_{ij}\,$: o custo unitário do transporte de $i$ para $j$.
O ideal é que a soma das quantidades fabricadas $(a_i)$ seja igual a soma das quantidades demandadas $(b_j)$ pelos consumidores, para que não seja necessário o uso de pátios de armazenamento para a operação de transporte, cujo o aluguel e manutenção aumentam os custos da operação.
O problema pode ser formulado por:
| função objetivo “Custo” | restrições | |
|---|---|---|
| $ \displaystyle C=\sum_{i=1}^{m}\sum_{j=1}^{n}d_{ij}x_{ij}$ | quantidade disponível na origem $i$ |
$\displaystyle \sum_{j=1}^{n}x_{ij}=a_i\,$ |
| quantidade demandada pelo destino $j$ |
$\displaystyle \sum_{i=1}^{m}x_{ij}=b_j\,$ | |
| Numérica | $ \displaystyle x_{ij} \geqslant 0 $ | |
Cujo o propósito é minimizar a função objetivo “Custo” $(C)$ para se obter a quantidade a transportar do fornecedor para o consumidor $ ( x_{ij} ) $ de maneira a se obter o menor custo $ ( C_{min} ) $.
O Problema da Designação
Consistem de um caso particular do problema do transporte em que:
- $m=n$;
- $ a_i=1 \quad \forall \, i $;
- $ b_j=1 \quad \forall \, j $;
Nesse contexto, o modelo assume a seguinte forma:
| função objetivo “Custo” | restrições | |
|---|---|---|
| $ \displaystyle C=\sum_{i=1}^{m}\sum_{j=1}^{n}d_{ij}x_{ij}$ | quantidade disponível na origem $i$ |
$\displaystyle \sum_{j=1}^{n}x_{ij}=1\,$ |
| quantidade demandada pelo destino $j$ |
$\displaystyle \sum_{i=1}^{m}x_{ij}=1\,$ | |
Numérica |
$ \displaystyle x_{ij} \geqslant 0 $ $ x_{ij}= \left\{\begin{matrix} 1, \quad \textbf{se } i=j \qquad\quad\,\,\, \\ 0, \quad \textbf{caso contrario} \end{matrix}\right.$ |
|
Referências
- M. Firmino de Medeiros Jr. Otimização de Sistemas, dca-UFRN, 2011.
- A. Izmailov; M. Solodov: Otimização – Vol. 2 – Métodos Computacionais. Instituto de Matemática Pura e Aplicada – IMPA, 2007.
- SILVA, E. M. et al. Pesquisa operacional: programação linear. São Paulo: Atlas, 1999.
- Bazaraa, M. S., Sherali, H.D., Shetty, C. M., Nonlinear programming: Theory and algorithms. 2nd ed. John Wiley, New York (NY), 1993.
- Bazaraa, M.S., Jarvis, J.J., e Sherali, H.D., Linear Programming and Network Flows. Wiley, 1990.
- Fletcher, R., Practical methods of optimization, John Wiley – Interscience, New York, 1987.
- Luenberger, D.: Introduction to Linear and Nonlinear Programming – Addison-Wesley, 1973.
