Os geradores síncronos a ímã permanente tem sido uma das opções preferidas para geração de energia eólica com grandes faixas de potência.

Esse tipo de gerador apresenta uma série de vantagens, se comparado aos geradores de indução ou mesmo aos geradores síncronos com rotor bobinado, dentre elas, destacam-se:
- Não necessitam de fontes de excitação externa, uma vez que o rotor possui imãs permanentes;
- Possibilidade de operação em baixa velocidade, para o caso de geradores com múltiplos pólos, não necessitando de caixas de engrenagens;
- Não apresenta perdas por efeito joule no enrolamento de campo (rotor), uma vez que não há circulação de corrente elétrica nesse enrolamento;
- Possibilitam, de acordo com a disposição dos ímãs, modificações nas características operacionais;
- Redução dos custos com manutenção, uma vez que não há mais a necessidade de escovas e caixas de engrenagens.
A estrutura básica de uma máquina síncrona constituída pelo enrolamento de armadura e um imã, situados no rotor e no estator, respectivamente.
Os enrolamentos do estator, a, b e c são trifásicos e defasados de $ 120^{\circ} $ entre si
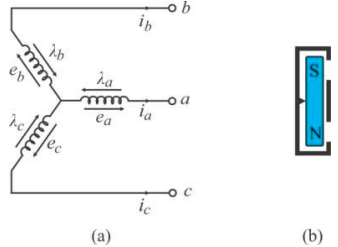
Considere o diagrama elétrico da máquina PMSG apresentado na figura abaixo
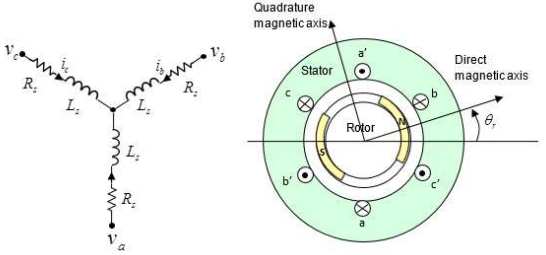
- O estator é composto por três enrolamentos trifásicos simétricos e equilibrados $ (R_s, \, L_s) $
- Já o rotor é composto por um ímã permanente orientado segundo o eixo direto.
O modelo da máquina síncrona (PMSG)
Para realizarmos a modelagem da máquina de indução, devemos seguir tais considerações:
1. A máquina é simétrica em relação ao estator e ao rotor;
2. Ângulos elétricos entre as bobinas é de $ 120^{\circ} $;
3. Correntes positiva geram fluxos positivos.

$ v_k^g = r_k i_k^g + \frac{d\phi_k^g}{dt} $
$ \phi_k^g \rightarrow $ Fluxo magnético em função das correntes e indutâncias
4. Máquina como receptor;
5. $ \theta_r = \frac{P}{2}\theta_m $
6. Distribuição senoidal do fluxo magnético;
7. Entreferro constante, relutância do entreferro independe de $ \theta_m $ (máquina de polos lisos).
8. A máquina não está na sua região de saturação.
$ \phi_t=\sum\phi_i \qquad $ e $ \qquad c_e = \frac{dW}{d\theta_m} $
Equações das tensões
$
\begin{bmatrix}
v_{sa} \\
v_{sb} \\
v_{sc}
\end{bmatrix}=
\begin{bmatrix}
R_s & 0 & 0 \\
0 & R_s & 0 \\
0 & 0 & R_s
\end{bmatrix}
\begin{bmatrix}
i_{sa} \\
i_{sb} \\
i_{sc}
\end{bmatrix}
+
\frac{d}{dt}
\begin{bmatrix}
\phi_{sa} \\
\phi_{sb} \\
\phi_{sc}
\end{bmatrix}
$
Em que $ v_{sabc} $, $ i_{sabc} $ e $ \phi_{sabc} $ são as tensões, corrente e fluxos concatenados do estator. $ R_s $ é a resistência dos enrolamentos estatóricos.
Equações dos fluxos
Os fluxos concatenados $ \phi_{sabc} $ podem ser descritos como:
$
\begin{bmatrix}
\phi_{sa} \\
\phi_{sb} \\
\phi_{sc}
\end{bmatrix}=
\begin{bmatrix}
L_{aa} & L_{ab} & L_{ac} \\
L_{ba} & L_{bb} & L_{bc} \\
L_{ca} & L_{cb} & L_{cc}
\end{bmatrix}
\begin{bmatrix}
i_{sa} \\
i_{sb} \\
i_{sc}
\end{bmatrix}
+
\phi_{pm}
\begin{bmatrix}
\cos(\theta_r) \\
\cos(\theta_r-2\pi/3) \\
\cos(\theta_r-4\pi/3)
\end{bmatrix}
$
Em que $ \theta_r $ é o ângulo elétrico do rotor e $ \phi_{pm} $ é o valor máximo do fluxo no entreferro da máquina.
O valor $ \phi_{pm} $ é definido como:
$ \phi_{pm} = \frac{60\cdot V_{pk}/k_{rpm}}{1000\cdot\sqrt{3}\cdot\pi\cdot P} $
Em que $ V_{pk}/k_{rpm} $ é a relação entre o valor máximo da f.e.m de linha da máquina e da sua velocidade mecânica. $ P $ é o número de polos. As indutâncias próprias e mútuas do estator são definidas como:
| Indutâncias Próprias | Indutâncias Mutuas |
| $ L_{aa}=L_s+L_0+L_2\cos(2\theta_r) \qquad\quad\,\,\, $ $ L_{bb}=L_s+L_0+L_2\cos(2\theta_r+2\pi/3) $ $ L_{cc}=L_s+L_0+L_2\cos(2\theta_r-2\pi/3) $ | $ L_{ab}=L_{ba}=-\frac{L_0}{2}+L_2\cos(2\theta_r-\frac{2\pi}{3}) $ $ L_{ac}=L_{ca}=-\frac{L_0}{2}+L_2\cos(2\theta_r+\frac{2\pi}{3}) $ $ L_{bc}=L_{cb}=-\frac{L_0}{2}+L_2\cos(2\theta_r) \qquad\,\, $ |
onde,
$ \qquad L_2 \rightarrow $ Indutância devido a saliência do rotor
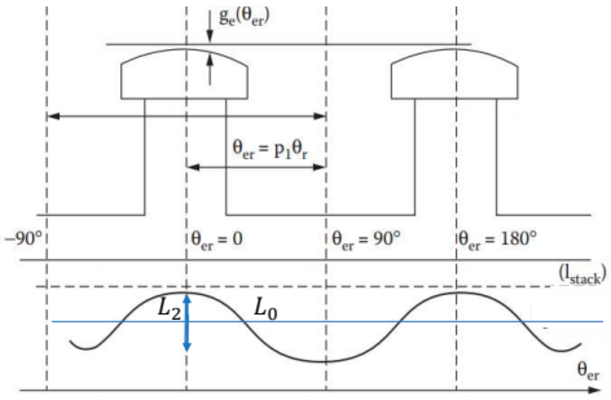
O conjugado eletromagnético da máquina PMSG pode ser dado por
$ T_{em}
=
-\frac{P}{2}L_S
\left[ i_{sa} \quad i_{sb} \quad i_{sc} \right]
\begin{bmatrix}
\sin(2\theta_r) & \sin(2\theta_r-\frac{2\pi}{3}) & \sin(2\theta_r+\frac{2\pi}{3}) \\
\sin(2\theta_r-\frac{2\pi}{3}) & \sin(2\theta_r+\frac{2\pi}{3}) & \sin(2\theta_r) \\
\sin(2\theta_r+\frac{2\pi}{3}) & \sin(2\theta_r) & \sin(2\theta_r-\frac{2\pi}{3})
\end{bmatrix}
\begin{bmatrix}
i_{sa} \\ i_{sb} \\ i_{sc}
\end{bmatrix}
-\frac{P}{2}\phi_{pm}
\left[ i_{sa} \quad i_{sb} \quad i_{sc} \right]
\begin{bmatrix}
\sin(\theta_r) \\
\sin(\theta_r-\frac{2\pi}{3}) \\
\sin(2\theta_r+\frac{2\pi}{3})
\end{bmatrix} $
Aplicações da Máquina Síncrona de Ímã Permanente (PMSG). (a) Locomotiva. (b) Aerogerador.
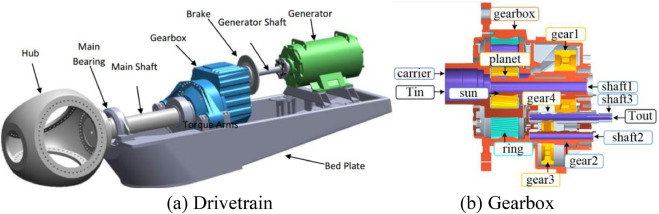

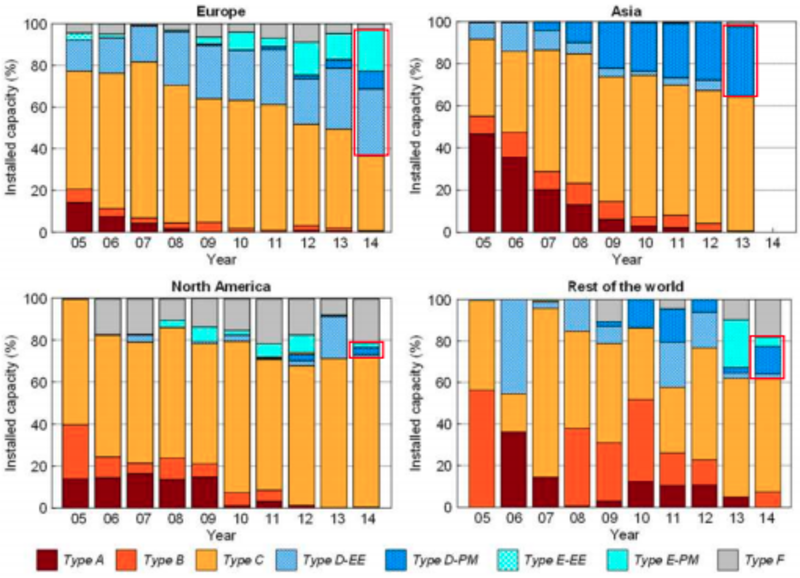
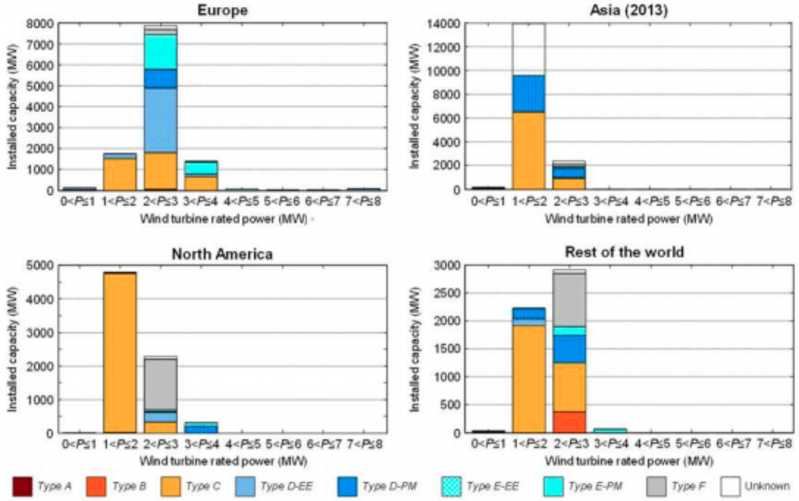
Turbinas eólicas (a) Drivetrain. (b) Gearbox (c) Tipos de turbinas eólicas de acordo com a configuração do drivetrain. (d) Evolução da parcela de capacidade instalada pela configuração de turbinas eólicas. (e) Configuração da turbina de acordo com a potência nominal em turbinas eólicas terrestres instaladas durante 2014 (durante 2013 na Ásia) Fonte: JRC database.
Modelo $ 0dq $
Uma alternativa para evitar essa dependência das indutâncias em relação a $ \theta_r $ e facilitar a análise do modelo, é transformá-lo em um modelo bifásico.
A transformação do sistema trifásico em bifásico por meio da transformada de Park, na qual as indutâncias sejam invariantes em relação à $ \theta_r $.
Fisicamente, a transformada de Park transforma enrolamentos estatóricos fixos em enrolamentos estatóricos girantes e enrolamentos rotóricos girantes em enrolamentos rotóricos pseudo estacionários.
Através dessa transformação pode-se representar cada armadura trifásica original do estator e do rotor por uma equivalente bifásica $ dq $, mais um enrolamento isolado.
Contudo, para que estas armaduras sejam equivalentes, as respectivas induções nos respectivos entreferros devem ser iguais.

Os eixos $ dq $ estão alinhados com os eixos do rotor e o eixo $ d $ se posiciona em um ângulo $ \theta_r $ em relação a um ponto de referência, no caso o eixo $ a $.
Utilizando a matriz de transformação de Park, os vetores das correntes, tensões e fluxos são representados da seguinte forma
$ [v_{s0dq}]=P[v_{sabc}] $
$ [i_{s0dq}]=P[i_{abc}] $
$ [\phi_{s0dq}]=P[\phi_{sabc}] $
$ [\phi_{pm0dq}]=P[\phi_{pmabc}] $
Equações de tensão
Das equações para o controle da máquina CA temos
$ v_{s0dq}
=
r_s i_{s0dq}
+
\frac{d\phi_{s0dq}}{dt}
+
\omega_r\begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0
\end{bmatrix}
\phi_{s0dq} \qquad $
O modelo da máquina PMSG pode ser simplificado utilizando a transformação de Park abc/dq na sua forma conservativa em potência dada por
$ \begin{bmatrix}
v_{sd} \\
v_{sq}
\end{bmatrix}
=
\begin{bmatrix}
R_d & 0 \\
0 & R_q
\end{bmatrix}
\begin{bmatrix}
i_{sd} \\
i_{sq}
\end{bmatrix}
+
\frac{d}{dt}
\begin{bmatrix}
\phi_{sd} \\
\phi_{sq}
\end{bmatrix}
+
\omega_r
\begin{bmatrix}
0 & -1 \\
1 & 0
\end{bmatrix}
\begin{bmatrix}
\phi_{sd} \\
\phi_{sq}
\end{bmatrix} $
logo,
$ v_{sd} = R_di_{sd} + \frac{d\phi_{sd}}{dt}-\omega_r\phi_{sq} \qquad\quad $
$ v_{sq} = R_qi_{sq} + \frac{d\phi_{sq}}{dt}+\omega_r\phi_{sd}^g \qquad\quad $
Equações do fluxo
Das equações para o controle da máquina CA temos
$ \phi_{s0dq} = l_{0dq}i_{s0dq} + \phi_{pmdq} $
onde,
| Fluxo no ímã permanente | $ \phi_{pmdq} = \begin{bmatrix} \sqrt{3/2}\phi_{pm} \\ 0 \end{bmatrix} \qquad\,\,\, $ |
| Impedância no PMSM | $ l_{0dq} = \begin{bmatrix} L_s & 0 & 0 \\ 0 & L_d & 0 \\ 0 & 0 & L_d \end{bmatrix} $ |
logo, os fluxo concatenados da máquina são dados por
$ \phi_{sd} = L_di_{sd}+\sqrt{\frac{3}{2}}\phi_{pm} $
$ \phi_{sq}=L_qi_{sq} \qquad\qquad\,\,\, $
Equações finais
| Tensões |
| $ v_{sd}^g = R_di_{sd}^g + \frac{d\phi_{sd}^g}{dt}-\omega_r\phi_{sq}^g \qquad\quad $ $ v_{sq}^g = R_qi_{sq}^g + \frac{d\phi_{sq}^g}{dt}+\omega_r\phi_{sd}^g \qquad\quad $ |
| Fluxos |
| $ \phi_{sd} = L_di_{sd}+\sqrt{\frac{3}{2}}\phi_{pm} \qquad\qquad\,\,\, $ $ \phi_{sq}=L_qi_{sq} \qquad\qquad\,\,\,\qquad\qquad\,\,\,\, $ |
Substituindo-se as definições dos fluxos concatenados nas equações de tensões, obtém-se
$ v_{sd} = R_di_{sd}+L_d\frac{di_{sd}}{dt}-\omega_rL_qi_{sq} \qquad\qquad\qquad\,\,\, $
$ v_{sq} = R_qi_{sq}+L_q\frac{di_{sq}}{dt}+\omega_r\left(L_di_{sd}+\sqrt{\frac{3}{2}}\phi_{pm}\right) $
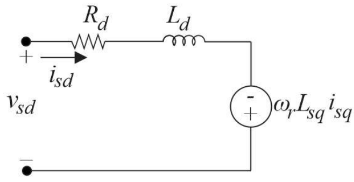

Circuito equivalente PMSG. (a) Grandezas em d. (b) Grandezas em q.
onde,
$ p_d = -\omega_rL_qi_{sq} \qquad\qquad\quad\,\,\, $
$ p_q = \omega_r\left(L_di_{sd}+\sqrt{\frac{3}{2}}\phi_{pm}\right) $
são perturbações a serem compensadas através de
$ v_{sd}^{‘} = v_{sd}-p_d = R_di_{sd}+L_d\frac{di_{sd}}{dt} $
$ v_{sq}^{‘} = v_{sq}-p_q = R_qi_{sq}+L_q\frac{di_{sq}}{dt} $
Usando a transformada de Laplace encontramos a planta do PMSG
$ v_{sd}^{‘}(s) = R_dI_{sd}(s)+L_dsI_{sd}(s) $
$ G_d(s)=\frac{I_{sd}(s)}{V_{sd}^{‘}(s)} = \frac{1}{L_d s + R_d} = \frac{1/L_d}{s + R_d /L_d } $
$ v_{sq}^{‘}(s) = R_qI_{sq}(s)+L_qsI_{sq}(s) $
$ G_q(s)=\frac{I_{sq}(s)}{V_{sq}^{‘}(s)} = \frac{1}{L_q s + R_q} = \frac{1/L_q}{s + R_q /L_q } $
Equações da potência
Temos que a potência elétrica é dada por
$ P_t = v_{sd}i_{sd}+v_{sq}i_{sq} $
Substituindo as tensões na máquina,
$ P_t = (R_di_{sd}^2+R_qi_{sq}^2) + \left( L_d\frac{di_{sd}}{dt}i_{sd}+L_q\frac{di_{sq}}{dt}i_{sq} \right) + \omega_r\left((L_d-L_q)i_{sq}i_{sd}+\sqrt{\frac{3}{2}}\phi_{pm}i_{sq} \right) $
onde,
| Perdas no cobre $ P_{cu} $ |
| $ (R_di_{sd}^2+R_qi_{sq}^2) $ |
| Taxa de variação da energia armazenada nas indutâncias do gerador $ P_i $ |
| $ \left( L_d\frac{di_{sd}}{dt}i_{sd}+L_q\frac{di_{sq}}{dt}i_{sq} \right) $ |
| Potência convertida da forma elétrica para mecânica (motor) $ P_g $ |
| $ \omega_r\left((L_d-L_q)i_{sq}i_{sd}+\sqrt{\frac{3}{2}}\phi_{pm}i_{sq} \right) $ |
Equações do conjugado
O conjugado da máquina PMSM no referencial síncrono $ dq $ pode ser dado por
$ c_e = \frac{P_g}{\omega_e}=\frac{P}{2}\left((L_d-L_q)i_{sq}i_{sd}+\sqrt{\frac{3}{2}}\phi_{pm}i_{sq} \right) $
A expressão do conjugado eletromagnético determina um acoplamento entre os eixo “d” e “q”.
O desacoplamento dos eixos é viabilizado utilizando a técnica de controle vetorial com orientação pelo campo rotórico (FOC).
O posicionamento do eixo “d” sobre o rotor da máquina PMSM permite zerar de forma controlada a corrente do eixo “d” e, consequentemente
$ c_e = \frac{P_g}{\omega_e}=\frac{P}{2}\left(\sqrt{\frac{3}{2}}\phi_{pm}i_{sq} \right) $
O conjugado passa a ser proporcional a corrente do eixo em quadratura da máquina bifásica $ i_{sq} $.
Por último, a modelagem da parte mecânica da máquina PMSM pode ser dada por
$ c_e-c_m=j\frac{d\omega_r}{dt}+F\omega_{r} $
Controle
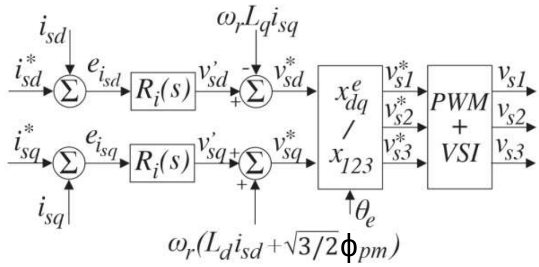
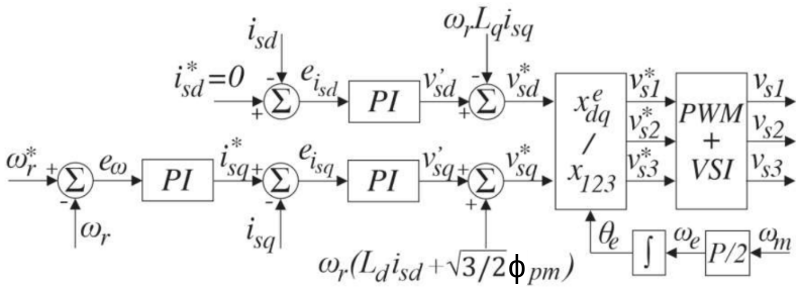
O esquema de controle do PMSG utiliza controladores do tipo PI (proporcional e integral) na regulação das correntes e na velocidade.
O controle das correntes do gerador é realizado no referencial síncrono.
O controlador de velocidade gera corrente de referência $ (i_{sq}^*) $ que, quando comparada com a corrente medida $ (i_{sq}) $, gera o sinal de erro a ser compensado pelo controlador PI da malha de velocidade.
No controle de corrente do eixo $ s $ a corrente de referência $ (i_{sd}^*) $ é comparada com a corrente medida $ (i_{sd}^* $ gerando o sinal de erro para ser compensado pelo controlador PI da malha de corrente.
Os sinais de tensão $ v_{sq} $ e $ v_{sd} $ são transformados para o referencial ‘abc’ por meio da transformada de Park.
$ c_e = \frac{P}{2} \left( \sqrt{\frac{3}{2}} \phi_{pm}i_{sq} \right) $
sendo,
$ c_e-c_m= J\frac{d\omega_r}{dt}+F\omega_{r} $
Considerando $ c_m $ como uma pertubação
$ c_e^{‘}= J\frac{d\omega_r}{dt}+F\omega_{r} $
A relação do conjugado e $ i_{sq} $ é dada por
$ c_e = \frac{P}{2} \left( \sqrt{\frac{3}{2}} \phi_{pm}i_{sq} \right) = K_li_{sq} $
onde,
$ K_l = \frac{P}{2} \left( \sqrt{\frac{3}{2}} \phi_{pm} \right) $
Desta forma
$ K_li_{sq}=J\frac{d\omega_r}{dt}+F\omega_r $
Usando a transformada de Laplace
$ K_lI_{sq}(s)=Js\Omega_r(s)+F\Omega_r(s) $
$ G_{\omega}(s)=\frac{\Omega_r(s)}{I_{sq}(s)}=\frac{K_l}{sJ+F/J}=\frac{K_l/J}{s+F/J}=\frac{b(s)}{a(s)} $
Para o sistema de primeira ordem temos
| Polo | $ p = \frac{F}{J} $ |
| Constante de tempo | $ \tau = \frac{1}{p} = \frac{J}{F} $ |
| Ganho | $ k = \frac{K_l}{J} $ |
O dimensionamento dos parâmetros do controlador PI da malha de velocidade (externa), pode ser realizado com base no método de alocação de polos.
O controlador $ PI $ é dado por
$ G_{PI,\omega}(s)=\frac{K_{\omega}\left( s+\frac{1}{\tau_{i\omega}} \right)}{s} = \frac{p(s)}{l(s)} $
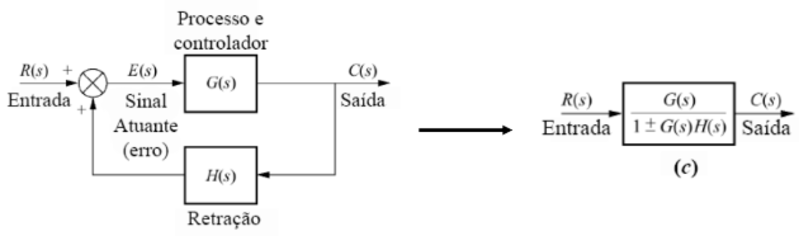
Os polos em malha fechada são dados por
$ A_{\omega}^*(s) = s^2\xi\omega_ns+\omega_n^2=b(s)p(s)+a(s)l(s) $
onde,
$ \qquad \omega_n \rightarrow $ Banda passante em malha fechada;
$ \qquad \xi \rightarrow $ Coeficiente de amortecimento.
Geralmente adota-se $ \xi = 0,707 $ para um $ MP = 5% $.
Resolvendo a equação diafontina em função dos ganhos do controlador
$ K_{\omega}=\frac{(2\xi\omega_nJ-F)}{K_l} $
$ \tau_{i\omega}=\frac{K_lK_{\omega}}{J\omega_n^2} $
A malha externa necessita ter um tempo de estabilização pelo menos 4 vezes maior que o tempo de estabilização do controle de corrente.
$ G_{i,d}(s)=\frac{I_{sd}(s)}{V_{sd}^{‘}(s)}=\frac{1}{sL_d+R_d}=\frac{1/L_d}{s+R_d/L_d}=\frac{p(s)}{l(s)} $
$ G_{i,q}(s)=\frac{I_{sq}(s)}{V_{sq}^{‘}(s)}=\frac{1}{sL_q+R_q}=\frac{1/L_q}{s+R_q/L_q}=\frac{p(s)}{l(s)} $
O dimensionamento dos parâmetros do controlador PI da malha de corrente (interna), pode ser realizado com base no método de alocação dos polos.
$ G_{PI,i}(s)=\frac{K_{idq}\left( s+\frac{1}{\tau_{idq}} \right)}{s} = \frac{p(s)}{l(s)} $
Os polos em malha fechada são dados por
$ A_{idq}^*(s) = s^2\xi_{dq}\omega_{ndq}s+\omega_{ndq}^2=b(s)p(s)+a(s)l(s) $
onde,
$ \qquad \omega_n \rightarrow $ Banda passante em malha fechada
$ \qquad \xi \rightarrow $ Coeficiente de amortecimento.
Resolvendo a equação diafontina em função dos ganhos do controlador
| Eixo d | Eixo q |
| $ K_{id}=2\xi_d\omega_{nd}L_d-R_s $ $ \tau_{id} = \frac{K_{id}}{L_d\omega_{nd}^2} \qquad\quad\,\, $ | $ K_{iq}=2\xi_q\omega_{nq}L_q-R_s $ $ \tau_{iq} = \frac{K_{iq}}{L_q\omega_{nq}^2} \qquad\quad\,\, $ |
A malha externa (controle de velocidade) necessita ter um tempo de estabilização pelo menos 4 vezes maior que o tempo de estabilização do controle de corrente (interno).
Referências
- Notas de aula do prof. dr. Caio Dorneles Cunha e prof. dr. Thiago de Oliveira Alves Rocha.
- Mohan, Undeland e Robbins, Power Electronics. Willey, 1989.
- W. Leonard, Control of Electrical Drives. Springer, 2001 2Ed.
- M. E. El-Hawary, Modeling and High Performance Control of Electric Machines. John Wiley & Sons, 2005.
- Chen-Mun Ong, Dynamic Simulation of Electric Machinery. Prentice-Hall, 1997.
- R. Krishnan, Eletric Motor Drives, Modeling, Analysis, and Control. Prentice-Hall, 2001.
- Ned Mohan, Máquinas Elétricas e Acionamentos. LTC, 2015.
- Ivo Barbi, Teoria Fundamental do Motor de Indução. Editora da UFSC/ELETROBRÁS, 1985.
