Em análise de algoritmos, a análise da eficiência assintótica de um algoritmo é explorada quando observamos tamanhos de entrada grande o suficiente para tornar relevante apenas a ordem de crescimento do tempo de execução, ou seja, na análise assintótica atenta-se a maneira como o tempo de execução de um algoritmo aumenta, à medida que o tamanho da entrada aumenta indefinidamente.
A ideia de complexidade assintótica foi introduzida em 1965 por Jack Edmonds (1934-) e consiste em uma função que define limites para a função $T(N)$ (complexidade local). Em outras palavras, a complexidade assintótica não fornece a complexidade local de um algoritmo, mas é capaz de estabelecer limites para o uso de recursos computacionais em sua execução. Desta forma, o conceito de complexidade assintótica viabiliza a comparação da complexidade entre diferentes algoritmos. Para tal, a complexidade assintótica é denotada através de uma COTA (ou classe de complexidade) que reduz detalhes da sua complexidade local, realçando apenas os aspectos relevantes da sua eficiência. (Figura 1).
Figura 1 – Cotas de diferentes algoritmos.
Fonte: Autor.
Geralmente, um algoritmo que é assintoticamente mais eficiente será a melhor escolha para todas as entradas, exceto as muitos pequenas.
Notação Big-O
Matematicamente, considerando um conjunto $A$ de algoritmos para a solução de um dado problema. A cada algoritmo $a \in A$ temos associado a função de avaliação correspondente $\text{test}(a)$. Nesse contexto, é de interesse identificar um algoritmo ótimo, ou seja, um algoritmo $o$ tal que $\text{test}(o)$ é melhor que $\text{test}(a)$ para todo $a \in A$. Assim, a análise da complexidade assintótica é usada na buscar do melhor algoritmo dentre um conjunto de algoritmos para solucionar um problema. Para isso se adota um conjunto de notações que auxiliam a formular conclusões sobre a comparação da complexidade de algoritmos. Essa notação é denominada notação Big-O e é apresentada abaixo:
- notação $O$ : limite assintótico superior;
- notação $\Omega$ : limite assintótico inferior;
- notação $\Theta$ : limite assintoticamente restrito;
- notação $o$ : limite assintoticamente superior não restrito;
- notação $\omega$ : limite assintoticamente inferior não restrito.
Notação $O$, Limite Assintótico Superior
Dadas funções assintoticamente não negativas $f$ e $g$, dizemos que $f$ está na ordem $O$ de $g$ e escrevemos $f=O(g)$ se:
$f(n) \leq c \cdot g(n)$
para algum $c$ positivo e para todo $n$ suficientemente grande.
Assim, diz-se que uma função limite superior $g(n)$ domina assintoticamente outra função $f(n)$ se existem duas constantes positivas $c$ e $n_0$ tais que, para qualquer $n \geq n_0$ temos, $f(n) \leq c \cdot g(n)$. Se escreve que $f(n)=O(g(n))$ ou $f(n) \in O(g(n))$ para expressar essa dominação (Figura 2).
Figura 2 – Notação $O$, limite assintótico superior.
Fonte: Autor.
Matematicamente, temos:
$O(g(n))=\{ \, f(n) : \exists \,\, c \,\, e \,\, n_0 > 0 \,\, | \,\, 0 \leq f(n) \leq c \cdot g(n) \,\, \forall \,\, n \geq n_0 \, \}$
Onde a notação $O$ pode ser lida de forma formal ou informal, como:
- $f(n)$ é da ordem no máximo $g(n)$ (formal);
- $f(n)$ é $O$ de $g(n)$ (informal);
- $f(n)$ é igual a $O$ de $g(n)$ (informal);
- $f(n)$ pertence a $O$ de $f(n)$ (formal).
Alguns exemplos da associação de COTAS e notação Big-O são apresentadas abaixo:
| Notação | Nome | Algoritmos |
|---|---|---|
| $O(1)$ | constante | Determinar se um número é par ou ímpar. Encontrar o valor máximo em um arranjo ordenado. |
| $O(\log{n})$ | logarítmica | Encontrar um valor em um arranjo ordenado usando busca binária. |
| $O(n)$ | linear | Encontrar um valor em um arranjo não ordenado usando busca sequencial. |
| $O(n\log{n})$ | linear logarítmica | Ordenar um arranjo usando quicksort. |
| $O(n^2)$ | quadrática | Ordenar um arranjo usando bubblesort. |
| $O(n^3)$ | cúbica | Multiplicar matrizes (produto matricial). |
| $O(c^n)$, $c>1$ | exponencial | Encontrar a solução exata para o problema do caixeiro viajante usando programação dinâmica. |
| $O(n!)$ | fatorial | Encontrar a solução exata para o problema do caixeiro viajante usando força bruta. |
Operações Básicas
$\qquad \qquad \qquad \,\, f(n)=O(f(n))$
$\qquad \qquad c \times Of(n)=O(f(n))$
$\, O(f(n))+O(f(n))=O(f(n))$
$\qquad \quad \,\, O(O(f(n)))=O(f(n))$
$\qquad \qquad \quad \,\, O(f(n))+O(g(n))=O(max(f(n),g(n)))$
$\qquad \quad \,\,\, O(f(n))O(g(n))=O(f(n)g(n))$
$\qquad \qquad \quad f(n)O(g(n))=O(f(n)g(n))$
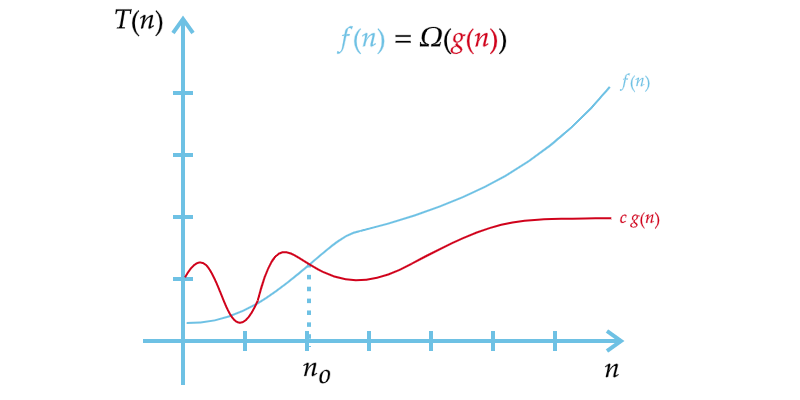
Notação $\Omega$, Limite Assintótico Inferior
Dadas funções assintoticamente não negativas $f$ e $g$, dizemos que $f$ está na ordem $\Omega$ de $g$ e escrevemos $f=\Omega (g)$ se:
$f(n) \geq c \cdot g(n)$
para algum $c$ positivo e para todo $n$ suficientemente grande.
Assim, diz-se que uma função limite inferior $g(n)$ domina assintoticamente outra função $f(n)$ se existem duas constantes positivas $c$ e $n_0$ tais que, para qualquer $n \geq n_0$ temos, $f(n) \geq c \cdot g(n)$. Se escreve que $f(n)=\Omega (g(n))$ ou $f(n) \in \Omega (g(n))$ para expressar essa dominação (Figura 3).
Figura 3 – Notação $\Omega$, limite assintótico inferior.
Fonte: Autor.
Matematicamente, temos:
$ \Omega (g(n))=\{ \, f(n) : \exists \,\, c \,\, e \,\, n_0 > 0 \,\, | \,\, 0 \leq c \cdot g(n) \leq f(n) \,\, \forall \,\, n \geq n_0 \, \}$
A notação $\Omega$ aparece na definição do conceito da notação $\Theta$ e não costuma ser vista sozinha fora deste escopo em análise de algoritmos uma vez que são de interesse as análises dos limites superiores ou o intervalo de operação dos algoritmos e não sua limitação inferior, ou seja, o limite inferior $\Omega$ não é importante para conclusões práticas sobre algoritmos enquanto a notação $O$ conclui que seu algoritmo é no máximo tão complexo a uma função que o limita.
Notação $\Theta$, Limite Assintoticamente Restrito
A notação $O$ fornece informações sobre a complexidade de um algoritmo, mas nem sempre revela algo importante. Constata-se esta realidade uma vez que não faz sentido para algum algoritmo de ordem $n$ dizer que suas complexidades são como, por exemplo:
$n \in O(2^n)$
$n \in O(n^n)$
Estas notações são verdadeiras, contudo, são também imprecisas. Assim, para estimar uma precisão sobre a complexidade de um algoritmo se defini um limite firme ou assintoticamente restrito,. Esse limite é conhecido como a notação $\Theta$.
Dadas funções assintoticamente não negativas $f$ e $g$, dizemos que $f$ está na mesma ordem de $g$ e escrevemos $f= \Theta (g)$ se $f=O(g)$ e $f= \Omega (g)$. Em outras palavras, $f=\Theta (g)$ significa que existe números positivos $c_1$ e $c_2$ tais que:
$c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)$
para todo $n$ suficientemente grande.
Assim, diz-se que uma função $g(n)$ está na mesma ordem de outra função $f(n)$ se existem três constantes positivas $c_1$, $c_2$ e $n_0$ tais que, para qualquer $n \geq n_0$ temos, $c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)$. Se escreve que $f(n)=\Theta (g(n))$ ou $f(n) \in \Theta (g(n))$ para expressar essa dominação (Figura 4).
Figura 4 – Notação $\Theta$, limite assintoticamente restrito.

Fonte: Autor.
Matematicamente, temos:
$ \Theta (g(n))=\{ \, f(n) : \exists \,\, c_1, \,\, c_2 \,\, e \,\, n_0 > 0 \,\, | \,\, 0 \leq c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n) \,\, \forall \,\, n \geq n_0 \, \}$
Logo,
$ f(n) \in \Theta (g(n)) $ se e somente se $ f(n) \in O (g(n)) $ e $ f(n) \in \Omega (g(n)) $
Contudo, cabe observar que nem toda função $\Omega$ é uma função $\Theta$ e nem toda função $O$ é uma função $\Theta$, mas uma função $\Theta$ é, necessariamente, $O$ e $\Omega$.
Notação $o$, Limite Assintoticamente Superior não Restrito
Toda as funções de $O$ que não definem um limite assintoticamente restrito pertence a “o”.
se $ f(n) \in O(g(n)) $ e $ f(n) \notin \Omega (g(n)) $ então $ f(n) \in o(g(n)) $
como, por exemplo:
| $f(n)$ | $g(n)$ | notação |
|---|---|---|
| $2n^2$ | $n^2$ | $2n^2 \in O(n^2)$ |
| $2n$ | $n^2$ | $2n^2 \in O(n^2)$ e $2n^2 \in o(n^2)$ |
| $\log(n)$ | $c^n$ | $\log(n) \in O(c^n)$ e $\log(n) \in o(c^n)$ |
Matematicamente, temos:
$ o(g(n))=\{ \, f(n) : \exists \,\, c \,\, e \,\, n_0 > 0 \,\, | \,\, 0 \leq f(n) < c \cdot g(n) \,\, \forall \,\, n \geq n_0 \, \}$
Logo, $ f(n) \in o(g(n)) $, o limite $ 0 \leq f(n) < c \cdot g(n) $ se mantém válido para todas as constantes $ c>0 $. Já $ f(n) \in O(g(n)) $, o limite $ 0 \leq f(n) \leq c \cdot g(n) $ se mantém válido para alguma constantes $ c>0 $.
Se $ f(n) \in o(g(n)) $ então:
$\displaystyle \lim_{ n \to \infty} \frac{f(n)}{g(n)}=0$
Notação $\omega$, Limite Assintoticamente Inferior não Restrito
Toda as funções de $\Omega$ que não definem um limite assintoticamente restrito pertence a “$\omega$”.
se $ f(n) \notin O(g(n)) $ e $ f(n) \in \Omega (g(n)) $ então $ f(n) \in \omega (g(n)) $
como, por exemplo:
| $f(n)$ | $g(n)$ | notação |
|---|---|---|
| $2n^2$ | $n^2$ | $2n^2 \in \Omega (n^2)$ |
| $2n^2$ | $n$ | $2n^2 \in \Omega (n^2) \,\,$ e $\,\, 2n^2 \in \omega(n^2)$ |
| $c^n$ | $\log (n)$ | $ c^n \in \Omega(\log (n)) \,\,$ e $\,\, c^n \in \omega(\log (n))$ |
Matematicamente, temos:
$ \omega (g(n))=\{ \, f(n) : \exists \,\, c \,\, e \,\, n_0 > 0 \,\, | \,\, 0 \leq c \cdot g(n) < f(n) \,\, \forall \,\, n \geq n_0 \, \}$
Logo, $ f(n) \in \omega (g(n)) $, o limite $ 0 \leq c \cdot g(n) < f(n) $ se mantém válido para todas as constantes $ c>0 $. Já $ f(n) \in \Omega (g(n)) $, o limite $ 0 \leq c \cdot g(n) \leq f(n) $ se mantém válido para alguma constantes $ c>0 $.
Se $ f(n) \in \omega (g(n)) $ então:
$\displaystyle \lim_{ n \to \infty} \frac{f(n)}{g(n)}=\infty$
As relações descritas entre os conjuntos que representam as notações apresentadas podem ser visualizadas a seguir:
Figura 5 – O conjunto de notações Big-O e a relação entre elas.

Fonte: Autor.
Limites para Comparar Ordens de Grandeza
O limite da razão das funções $f(n)$ e $g(n)$ podem levar a três casos:
$ \displaystyle \lim_{ n \to \infty} \frac{f(n)}{g(n)} = \left\{ \begin{matrix} 0, \, f(n) \text{ tem ordem de grandeza menor que g(n);} \\ c>0, \, f(n) \text{ tem a mesma ordem de grandeza que g(n);} \\ \infty, \, f(n) \text{ tem ordem de grandeza maior que g(n);} \end{matrix} \right. $
Caso tenhamos uma indeterminação da forma $\frac{\infty}{\infty}$, utiliza-se da regra de L’Hôpital para sua aferição:
$\displaystyle \lim_{ n \to \infty} \frac{f(n)}{g(n)}=\lim_{ n \to \infty} \frac{f'(n)}{g'(n)}$
Comparação de funções
Muitas das propriedades relacionais de números reais também se aplicam a comparações assintótica. No caso das propriedades seguintes, suponha $f(n)$ e $g(n)$ sejam assintoticamente positivas.
Reflexividade
$f(n)=\Theta(f(n))$
$f(n)=O(f(n))$
$f(n)=\Omega(f(n))$
Simetria
$f(n)=\Theta(g(n))$ se e somente se $g(n)=\Theta(f(n))$
Simetria de Transposição
$f(n)=O(g(n))$ se e somente se $g(n)=\Omega(f(n))$
$f(n)=o(g(n))$ se e somente se $g(n)=\omega(f(n))$
Transitividade
$f(n)=\Theta(g(n))$ e $g(n)=\Theta(b(n))$ $\Rightarrow$ $f(n)=\Theta(b(n))$
$f(n)=O(g(n))$ e $g(n)=O(b(n))$ $\Rightarrow$ $f(n)=O(b(n))$
$f(n)=\Omega(g(n))$ e $g(n)=\Omega(b(n))$ $\Rightarrow$ $f(n)=\Omega(b(n))$
$f(n)=o(g(n))$ e $g(n)=o(b(n))$ $\Rightarrow$ $f(n)=o(b(n))$
$f(n)=\omega(g(n))$ e $g(n)=\omega(b(n))$ $\Rightarrow$ $f(n)=\omega(b(n))$
Padrões de Identificação de Passos em um Algoritmo
Uma sequência sem laço ou recursão conta passo constante $O(1)$:
Quando divide o problema pela metade conta passo logarítimo $O(\log{n})$:
Um único laço com $n$ passos inteiros constante conta passo linear $O(n)$:
Dois laços de tamanho $n$ alinhados conta passo quadrático $O(n^2)$:
Concluindo, a complexidade assintótica é um conceito utilizado na análise da complexidade de um algoritmo e que é largamente empregado, principalmente quando a natureza de sua complexidade é matematicamente árdua ou dificilmente capaz de ser formulada para análise exata de seu comportamento. O conceito de complexidade assintótica e o da notação Big-O propiciam uma metodologia capaz de estimar o crescimento da demanda de recursos computacionais por um algoritmo sem ter uma noção exata de seu comportamento, viabilizando o estudo da resolução de um problema por diferentes algoritmos através da observação de seu comportamento e da comparação entre suas eficiências (Figura 6).
Figura 6 – Complexidade assintóticas de diferentes algoritmos.

Fonte: Autor.
Referências
- PIVA JÚNIOR, Dilermando (et al). Estrutura de dados e técnicas de programação. 1. ed. Rio de Janeiro, RJ: Campus, 2014. 399 p. ISBN: 9788535274370.
- CORMEN, Thomas H et al. Algoritmos: teoria e prática. Rio de Janeiro: Elsevier, 926 p. ISBN: 9788535236996.
- TOSCANI, Laira Vieira; VELOSO, Paulo A. S. Complexidade de algoritmos: análise, projeto e métodos. 3. ed. Porto Alegre: Bookman, 2012. 261 p. (Série livros didáticos informática UFRGS, 13) ISBN: 9788540701380.
- ASCENCIO, Ana Fernanda Gomes. Estruturas de dados: algoritmos, análise da complexidade e implementações em Java e C/C++. São Paulo: Pearson, c2010. 432 p. ISBN: 9788576052216, 978857605816.
- BRASSARD, Gilles; BRATLEY, Paul. Fundamentals of algorithmics. Englewood Cliffs: Prentice Hall, c1996. xx, 524 p. ISBN: 0133350681.