Análise de Algoritmos

Fonte: Unsplash/Kevin Ku

Um algoritmo pode ser definido por:

Uma sequência bem definida de procedimentos computacionais (passos) que levam uma entrada a ser transformada em uma saída.
Cormen et al. 1991

A análise de algoritmos é a atividade de avaliar a qualidade de um algoritmo para a resolução de um problema. Nesta análise são comparados diversos algoritmos que resolvem um mesmo problema para então discernir qual o mais indicado à sua resolução.

Duas maneiras de se comparar algoritmos são através de seu desempenho (complexidade) e de sua solução (completude).

A Solução de um Algoritmo

Em um algoritmo a saída deve corresponder a uma solução válida para o problema. A solução de um algoritmo refere-se a resposta de um algoritmo para uma instância de um problema.

A análise da solução de um algoritmo consiste em saber o quão boa é a resposta de um algoritmo para uma instância de um problema, indiferente da quantidade de passos necessários para a sua obtenção.

O Desempenho de um Algoritmo

O desempenho (complexidade) de um algoritmo refere-se a quantidade de recursos computacionais utilizados para que este algoritmo obtenha a solução para um problema.

Em um computador, um processador é capaz de processar várias instruções em uma sequência. Isso significa que o processador leva um tempo para executar cada instrução. O tempo de processamento de um algoritmo deve ser finito. Assim, existe uma quantidade limitada de instruções que um processador é capaz de processar em uma quantidade arbitrada de tempo. Desta forma, quanto maior o número de instruções contidas em um algoritmo, mais tempo será necessário para a obtenção de uma solução.

Neste contexto, a análise de desempenho de um algoritmo consiste em saber a quantidade de instruções que um algoritmo precisa para retornar a solução de uma ou várias instâncias de um problema, indiferente a qualidade de sua solução.

Eficiência de um Algoritmo

A eficiência de um algoritmo é a medida quantitativa inversa da quantidade de instruções requeridas para a execução do algoritmo. Quanto maior a eficiência de um algoritmo, menos instruções são necessárias, portanto, menos recursos computacionais são gastos.

Os dois principais métodos de mensuração da eficiência de um algoritmo são:

O método experimental;
O método analítico.

O Método Experimental

O método experimental consiste em:

implementar diversos algoritmos;
executar os algoritmos um grande número de vezes;
analisar os resultados.

No método experimental, o tempo de execução não depende somente do algoritmo, mas do conjunto de instruções do processador, a qualidade do compilador, a habilidade do programador etc. Neste método, o tempo de processamento pode ser mensurado através do próprio sistema operacional ou por meio de um algoritmo de testes.

O algoritmo de testes avalia a complexidade do algoritmo para várias instâncias de um problema, cada qual com diferentes ordens de grandeza $(n)$. A dificuldade em se utilizar algoritmos de testes é a limitação no número de testes que podem ser realizados por eles, ou seja, caso exista alguma instância de ordem $n$ não testada, não será possível saber o comportamento do algoritmo simplesmente por esta instância não ter sido testada.

O Método Analítico

O objetivo do método analítico é encontrar funções matemáticas que descrevem o crescimento do tempo de processamento dos algoritmos em relação ao tamanho da entrada e comparar estas funções (Figura 1).

Figura 1 – Análise quantitativa do desempenho de um algoritmo.Fonte: Autor.

onde:

$n$ é o ordem da instância do problema;
$T(n)$ é a função matemática que descreve o crescimento do tempo de execução do algoritmo.

Estas curvas podem ser obtidas por meio da modelagem matemática do problema deduzida a partir do próprio algoritmo ou a partir de dados estimados de forma empírica, ou seja, implementando o programa, coletando os resultados e seguir montando estas curvas estatisticamente com estes resultados.

As curvas apresentam características diferentes para cada algoritmo utilizado para a solução de um mesmo problema. Por meio do gráfico podemos observar que para um problema do mesmo tamanho e com as mesmas características, um algoritmo pode apresentar soluções bastante diversas.

A observação de tamanhos de entradas grande o suficiente, de forma que apenas a ordem de crescimento do tempo de processamento seja relevante é conhecida como a análise assintótica da eficiência de um algoritmo.

A análise assintótica pode ser o fator determinante do sucesso de um software. O google é um exemplo de alta eficiência dos algoritmos de buscas utilizados pela empresa, superiores aos demais concorrente e um dos responsáveis pelo seu sucesso no mercado.

Aplicação da Análise de um Algoritmo

A análise de um algoritmo é realizada através da aplicação das técnicas de análise do desempenho e da solução de um algoritmo.

Para algoritmos mais simples é possível utilizar de análise matemática através de deduções de fórmulas ou provas matemáticas (método analítico). O método analítico é o mais complexo porque dele é possível obter garantias de que o algoritmo sempre obterá soluções de qualidade com um desempenho determinístico.

Em algoritmos mais complexos muitas vezes não se existe uma definição completa para o problema tratado. Como, por exemplo, o sistema de usuários de um e-commence para compras online (amazon, mercado livre, submarino etc), que não utilizam de uma definição formal para obtenção da solução de seus problemas. Para tal, o que existe é uma série de estudos em engenharia de software para o levantamento de requisitos que vai tentar construir estas definições, o que torna sua abordagem mais complexa. Da mesma forma existem aplicações, tais como os jogos de computador, tão complicadas e dotadas de tantos aspectos diferentes que se torna difícil utilizar da análise matemática para obter garantias de quão bom um algoritmo é quando comparado a outro. Nessa conjuntura, para algoritmos mais complexos é utilizada uma estratégia de análise empírica (ou subjetiva). A análise empírica ou empirismo adota o método experimental para a observação, ou seja, adota uma análise estatística para obter a soluções de um problema com um desempenho estimado. Na análise empírica, as estatísticas são retiradas das execuções do método experimental. Das estatísticas obtidas é estimada a expressão que reflete o comportamento do algoritmo (Gamers Benchmarking). Na maioria das vezes, a escolha de um algoritmo é feita através de critérios empíricos como:

facilidade de compreensão, codificação e depuração;
eficiência na utilização dos recursos do computador e rapidez.

Logo, um problema pode ser resolvido através de diversos algoritmos (análise de completude). Contudo, o fato de um algoritmo resolver um dado problema não significa que a sua solução seja aceitável na prática (análise da complexidade). Assim, a análise de um algoritmo fornece uma medida objetiva da solução de um problema de forma proporcional ao tempo de processamento do algoritmo.

Ordem $(n)$	Método de Cramer $T_C(n)$	Método de Gauss $T_G(n)$
2	22us	50us
3	102us	159us
4	456us	353us
5	2,35ms	666us
10	1,19min	4,95ms
20	15255 séculos	38,65ms

Neste contexto, analisar um algoritmo significa prever os recursos de que o algoritmo necessitará para obtenção da solução de um problema e estimar o seu tempo de processamento. Em outras palavras, encontrar a eficiência de um algoritmo pela observação da quantidade de recursos que ele consome através de alguns critérios, tais quais:

operações de entrada e saída;
operações aritméticas;
operações lógicas e relacionais;
movimentação de dados entre os componentes;
atribuições, declarações de métodos e variáveis;
estrutura de decisão e repetição;
chamadas de métodos etc.

aplicando os seguintes procedimentos:

definir a ordem $(n)$ do problema;
contabilizar o custo de cada linha, assumindo que cada operação tem 1 custo (ou unidade de tempo);
contabilizar quantas vezes (no máximo) cada linha é executada;
somar o custo total de cada linha.

Para a análise de um algoritmo é necessário a análise de todas as suas condições possíveis.

Tipicamente, são avaliadas três condições para descrever um algoritmo:

melhor caso (custo mínimo);
pior caso (custo máximo);
caso médio (custo médio).

Diferentes algoritmos variam em cada um destes aspectos. Como, por exemplo, alguns algoritmos de ordenação possuem a mesma complexidade de “caso médio”, porém tem um “pior caso” pior que o outro. Existem situações em que isso não é um problema e outras em que o “pior caso” de um algoritmo é muito ruim. Com estas informações podemos discutir a qualidade dos algoritmos em uma determinada situação (Figura 2).

Figura 2 – Análise do algoritmo de busca binária.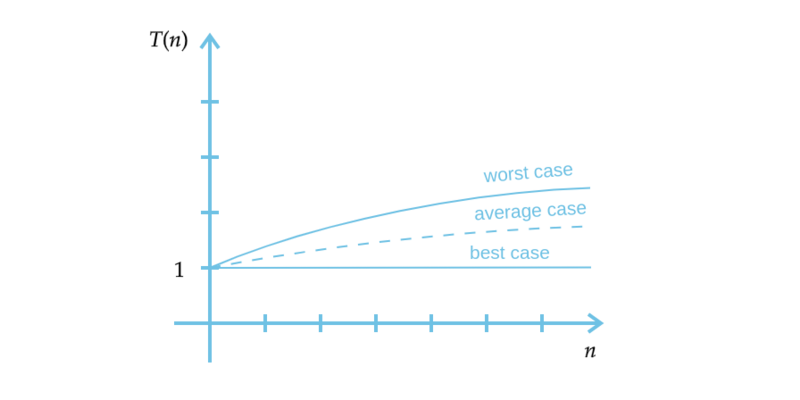Fonte: Autor.

Referências

PIVA JÚNIOR, Dilermando (et al). Estrutura de dados e técnicas de programação. 1. ed. Rio de Janeiro, RJ: Campus, 2014. 399 p. ISBN: 9788535274370.
CORMEN, Thomas H et al. Algoritmos: teoria e prática. Rio de Janeiro: Elsevier, 926 p. ISBN: 9788535236996.
TOSCANI, Laira Vieira; VELOSO, Paulo A. S. Complexidade de algoritmos: análise, projeto e métodos. 3. ed. Porto Alegre: Bookman, 2012. 261 p. (Série livros didáticos informática UFRGS, 13) ISBN: 9788540701380.
ASCENCIO, Ana Fernanda Gomes. Estruturas de dados: algoritmos, análise da complexidade e implementações em Java e C/C++. São Paulo: Pearson, c2010. 432 p. ISBN: 9788576052216, 978857605816.
BRASSARD, Gilles; BRATLEY, Paul. Fundamentals of algorithmics. Englewood Cliffs: Prentice Hall, c1996. xx, 524 p. ISBN: 0133350681.