Análise dos Algoritmos de Busca

Fonte: Unsplash/Kevin Ku

O problema de busca consiste em avaliar se um elemento de mesmo tipo de uma sequência está contido, ou não, na sequência.

Dois algoritmos para a solução do problema de busca são o algoritmo de busca sequencial e o algoritmo de busca binária.

Para analisar os algoritmos de busca e saber qual é o melhor é necessário uma observação geral do problema dada todas as instâncias com alguma característica em comum.

Sabendo que o domínio do problema de busca são o conjunto das sequências podemos refletir sobre qual o aspecto de uma sequência tem maior impacto sobre a dificuldade de se realizar uma busca dentro dela.

Comumente, a principal característica avaliada no problema de busca é o tamanho do espaço de busca. No caso específico de uma sequência, o tamanho do espaço de busca se refere ao número de elementos $(n)$.

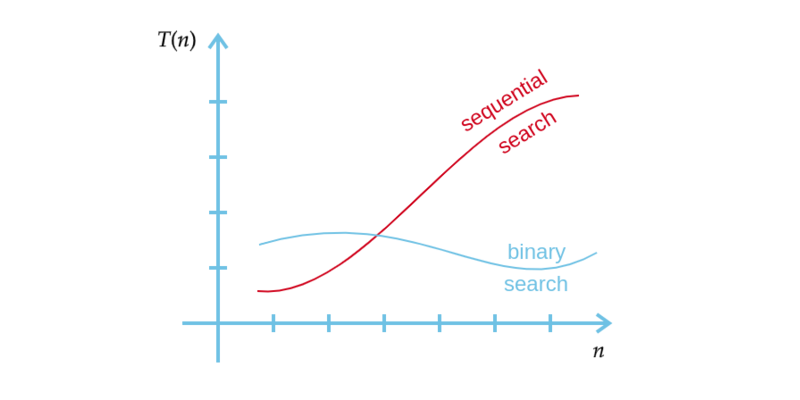
O foco da análise é a obtenção da expressão que apresente o número de execuções de um pedaço elementar do algoritmo de busca (operação de comparação) dado o número $(n)$ de elementos de uma sequência. O resultado desta expressão para cada algoritmo pode ser observado graficamente (Figura 1). O esforço realizado pelo algoritmo de busca é calculado a partir da quantidade de vezes que a operação de comparação é executada.

Figura 1 – Análise dos algoritmos de busca.

Fonte: Autor.

onde

$n$ é o número de elementos da sequência;
$T(n)$ o número de execuções de um pedaço elementar do algoritmo para obter a solução de um problema.

Estas curvas podem ser obtidas por meio da modelagem matemática do problema deduzida a partir do próprio algoritmo ou a partir de dados estimados de forma empírica, ou seja, implementando o programa, coletando os resultados e seguir montando estas curvas estatisticamente com estes resultados.

As curvas apresentam características diferentes para cada algoritmo utilizado para a solução de um mesmo problema. Por meio do gráfico podemos observar que para um problema do mesmo tamanho e com as mesmas características, um algoritmo pode apresentar soluções bastante diversas.

No problema de busca, dependendo da chave de busca, um algoritmo pode ser melhor do que o outro. Isso significa que para cada condição não basta apenas uma avaliação.

Análise dos Algoritmos de Busca Sequencial

Para os algoritmos de busca sequencial em sua implementação iterativa em C:

Aplicando o método experimental para a análise dos algoritmos, temos:

Linha	Custo	Repetição	Total
10 ou 26	1	1	1
11 ou 27	1	n+1	n+1
12 ou 28	1	n	n
14 ou 30	1	1	1
15 ou 31	1	1	1
Soma			2n+4

Logo,

$T(n)=2n+4$

(1)

Assim, temos que as condições que os descrevem são:

Melhor caso: $T(n)=4$;
Pior caso: $T(n)=2n+4$.

O caso médio depende das probabilidades associadas às possíveis entradas para o algoritmo. Assumindo que $x$ está em $A$:

$T_A(n)=p_1+2p_2+\cdots+n \times p_n$

(2)

onde $p_i$ é a probabilidade de $x$ estar na posição $i$.

Na busca sequencial as probabilidades são iguais a:

$p_i=1/n$

(3)

Substituindo (3) em (2), temos que o caso médio da busca sequencial tem complexidade de:

$T_A(n)=(1/n)(1+2+\cdots+n)=(n+1)/2$

(4)

Logo, uma pesquisa bem-sucedida examina aproximadamente metade dos registros.

A taxa de crescimento de um algoritmo é representada através de cotas que são funções mais simples. A ordem de crescimento do tempo de processamento de um algoritmo fornece uma caracterização simples da eficiência do algoritmo. Desta forma, em um função de complexidade:

se desprezam os termos de baixa ordem;
se ignora o coeficiente constante

Portanto, o tempo de processamento do algoritmo tem cota igual a $N$. Assim, podemos estimar que o algoritmo de busca sequencial tem complexidade de:

$T(n)=n$

(5)

Para os algoritmos de busca sequencial em sua implementação recursiva em C:

Adotando o método analítico para a análise dos algoritmos, observa-se que as condições iniciais que os descrevem são:

Melhor caso: elemento encontrado no primeiro loop da recursão. Linhas 4 e 11 com $T(n)=1$;
Pior caso: busca recursiva em todos os elementos da sequência. Linhas 5 e 12 com $T(n)=1+T(n-1)$.

Analisando a dinâmica dos algoritmos de busca sequenciais e a sequência em seu “pior caso” dado por:

$T(n)=1+T(n-1)$

(6)

Podemos encontrar a expressão de $T(n)$ a ser representada graficamente.

Pelo princípio da indução finita temos que a sequência (6) pode ser representada pela expressão:

$T(n)=k+T(n-k), \qquad k \geq 1 $

(7)

Em (7), quando $k=n$ temos que:

$T(n)=n+T(0)$

(8)

Pela dinâmica do algoritmo sabemos que:

$T(0)=0$

(9)

Logo, substituindo (9) em (8), o “pior caso” do algoritmo de busca sequencial é expresso matematicamente por:

$T(n)=n$

(10)

Assim, reescrevendo as condições que descrevem o algoritmo de busca sequencial (Figura 2) concluímos que:

Melhor caso: $T(n)=1$;
Pior caso: $T(n)=n$.

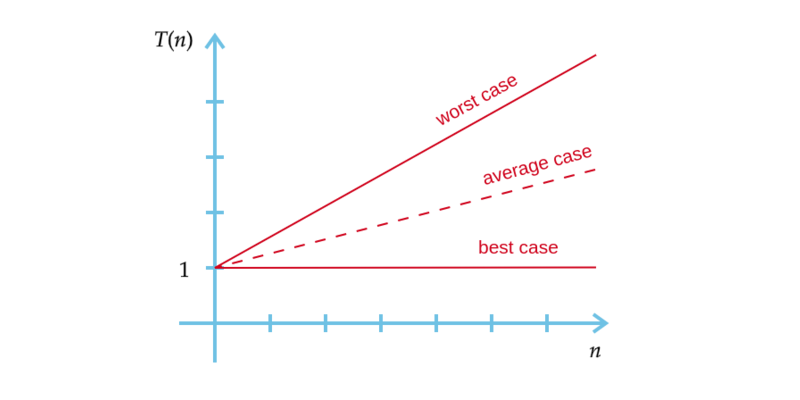
Figura 2 – Análise dos algoritmos de busca sequenciais.

Fonte: Autor.

No gráfico, estimamos o caso médio como sendo a presença do valor na metade da sequência $(n/2)$. Analisando o gráfico dos algoritmos de busca sequenciais já é possível ter uma ideia do crescimento do número de operações dado o tamanho da sequência.

Análise do Algoritmo de Busca Binária

Para o algoritmo de busca binária em sua implementação recursiva em C:

Adotando o método analítico para a análise dos algoritmos, observa-se que as condições iniciais que os descrevem são:

Melhor caso: elemento encontrado no primeiro loop da recursão. Linhas 4 com $T(n)=1$;
Pior caso: busca recursiva em todas as medianas da sequência. Linhas 5 e 6 com $T(n)=1+T(n/2)$.

Analisando a dinâmica dos algoritmos de busca sequenciais e a sequência em seu “pior caso” dado por:

$T(n)=1+T(n/2)$

(11)

Novamente, podemos encontrar a expressão de $T(n)$ a ser representada graficamente.

Pelo princípio da indução finita temos que a sequência (11) pode ser representada pela expressão:

$T(n)=k+T(n/2^k), \qquad k \geq 1$

(12)

Em (12), quando $n/2^k=1$ temos que:

$T(n)=\log{n}+T(1)$

(13)

Pela dinâmica do algoritmo sabemos que:

$T(1)=1$

(14)

Logo, substituindo (14) em (13), o “pior caso” do algoritmo de busca sequencial é expresso matematicamente por:

$T(n)=\log{n}+1$

(15)

Assim, reescrevendo as condições que descrevem o algoritmo de busca sequencial (Figura 3) concluímos que:

Melhor caso: $T(n)=1$;
Pior caso: $T(n)=\log{n}+1$.

Figura 3 – Análise do algoritmo de busca binária.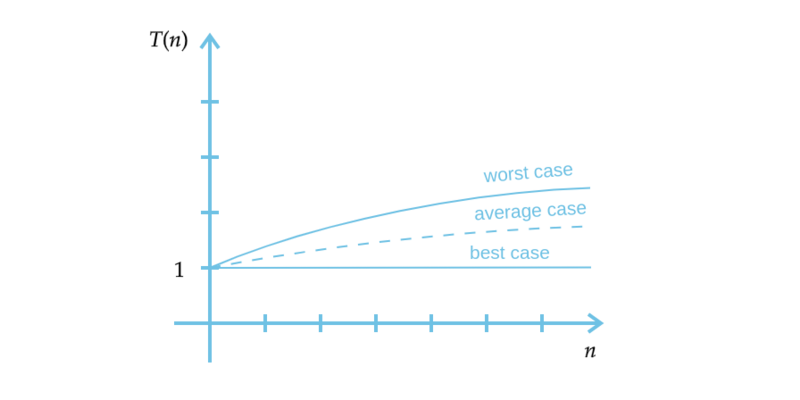Fonte: Autor.

No gráfico, estimamos o caso médio como sendo a presença do valor entre o melhor e o pior caso, fica o convite ao leitor explorar a complexidade do cálculo de caso médio. Analisando o gráfico do algoritmo de busca binária é possível observar que o crescimento do número de operações dado o tamanho da sequência é inferior ao do algoritmo de busca sequencial em seu “pior caso” e para o seu “caso médio”. Isso significa que o comportamento de custo do algoritmo de busca binária é melhor que o algoritmo de busca sequencial.

A análise de algoritmos nos permite comparar diferentes algoritmos com diferentes expressões que os representem. Para o problema de busca, a complexidade dos algoritmos de busca sequencial e binária são representadas pelas seguintes expressões:

Casos	Busca Sequencial	Busca Binária
Melhor Caso	$T(n)=1$	$T(n)=1$
Pior Caso	$T(n)=n$	$T(n)=\log{n}+1$

Referências

PIVA JÚNIOR, Dilermando (et al). Estrutura de dados e técnicas de programação. 1. ed. Rio de Janeiro, RJ: Campus, 2014. 399 p. ISBN: 9788535274370.
CORMEN, Thomas H et al. Algoritmos: teoria e prática. Rio de Janeiro: Elsevier, 926 p. ISBN: 9788535236996.
TOSCANI, Laira Vieira; VELOSO, Paulo A. S. Complexidade de algoritmos: análise, projeto e métodos. 3. ed. Porto Alegre: Bookman, 2012. 261 p. (Série livros didáticos informática UFRGS, 13) ISBN: 9788540701380.
ASCENCIO, Ana Fernanda Gomes. Estruturas de dados: algoritmos, análise da complexidade e implementações em Java e C/C++. São Paulo: Pearson, c2010. 432 p. ISBN: 9788576052216, 978857605816.
BRASSARD, Gilles; BRATLEY, Paul. Fundamentals of algorithmics. Englewood Cliffs: Prentice Hall, c1996. xx, 524 p. ISBN: 0133350681.

ELETRIZADO