O fatorial de um número representa a quantidade de possibilidade de arranjos de um conjunto com “n” elementos.
O algoritmo para o cálculo fatorial de um número em sua implementação recursiva em C é:
Da sua implementação recursiva é possível observar que durante a execução do algoritmo vários registros de ativação são empilhados na memória a cada chamada recursiva da função, acumulando-os. Já quando a função termina, o registro de ativação é desempilhado e a execução volta ao subprograma que chamou a função (Figura 1).
Figura 1 – A pilha de execução do algoritmo para o cálculo de 4! em sua implementação recursiva.
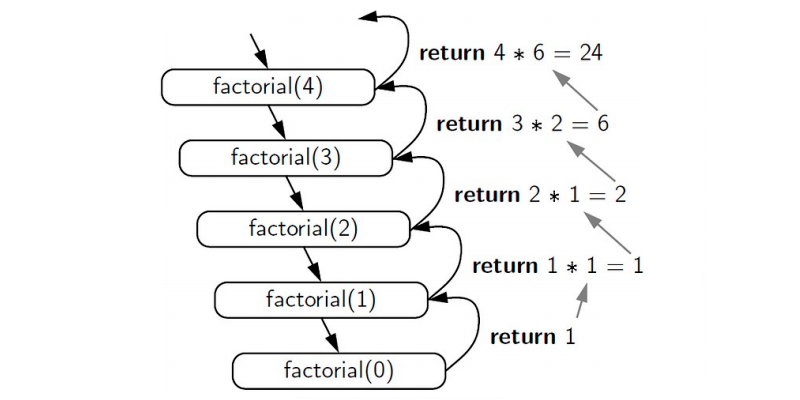
Fonte: codecademy.
Desta forma, o custo em espaço de memória aumenta a cada chamada recursiva da função. Logo, a complexidade assintótica de espaço e de tempo do algoritmo recursivo para o cálculo fatorial de um número são ambos $O(n)$.
O algoritmo para o cálculo fatorial de um número em sua implementação iterativa em C é:
Da implementação iterativa do algoritmo para o cálculo fatorial é possível observar que a complexidade assintótica de espaço para o mesmo algoritmo em sua implementação iterativa é $O(1)$ e a complexidade assintótica de tempo permanece $O(n)$.
Assim, comparando a eficiência de suas implementações, temos:
| Implementação | Custo de Espaço | Custo de Tempo |
|---|---|---|
| iterativa | $O(1)$ | $O(n)$ |
| recursiva | $O(n)$ | $O(n)$ |
Portanto, a implementação iterativa para o cálculo fatorial de um número é mais eficiente que sua implementação recursiva.
Referências
- PIVA JÚNIOR, Dilermando (et al). Estrutura de dados e técnicas de programação. 1. ed. Rio de Janeiro, RJ: Campus, 2014. 399 p. ISBN: 9788535274370.
- CORMEN, Thomas H et al. Algoritmos: teoria e prática. Rio de Janeiro: Elsevier, 926 p. ISBN: 9788535236996.
- TOSCANI, Laira Vieira; VELOSO, Paulo A. S. Complexidade de algoritmos: análise, projeto e métodos. 3. ed. Porto Alegre: Bookman, 2012. 261 p. (Série livros didáticos informática UFRGS, 13) ISBN: 9788540701380.
- ASCENCIO, Ana Fernanda Gomes. Estruturas de dados: algoritmos, análise da complexidade e implementações em Java e C/C++. São Paulo: Pearson, c2010. 432 p. ISBN: 9788576052216, 978857605816.
- BRASSARD, Gilles; BRATLEY, Paul. Fundamentals of algorithmics. Englewood Cliffs: Prentice Hall, c1996. xx, 524 p. ISBN: 0133350681.





