A primeira coisa que precisamos saber para definir o que é um dado é o conceito de registro. Um registro é uma estrutura física, é algo que existe, é algo tátil, é o contrário de algo abstrato. Um registro sendo algo que existe, possui algumas características, sendo a principal delas uma condição de estado dentre várias possibilidades de estado, figura 01.
Figura 01 – Uma lâmpada pode ser considerada um registro de dois estados, acesa ou apagada.
Fonte: embarcados.
Para o estudo da computação adotemos um tipo de registro, o registro binário. O registro binário possui dois estados, estes estados são: ligado “1” ou desligado “0”.
Em computação um dado é apresentado como um estado de um registro e um conjunto de dados podem ser definidos como uma representação de fatos, conceitos ou instruções de maneira formalizada que devem ser adequados para a comunicação, interpretação, ou de transformação pelo homem ou dispositivo eletrônico. Um dado se torna útil quando passível de relação com algo da realidade, aspecto de um problema ou um contexto, figura 02. Quando isso ocorre, um dado pode ser chamado de informação.
Figura 02 – Os estados das lâmpadas de um semáforo transmitem instruções aos condutores de veículos.
Fonte: mundo das mesinhas.
Uma vez relacionados os conceitos de dados e informação podemos observar que nem todo tido tipo de informação pode ser representada por um registro binário (“0” e “1”) como, por exemplo, o número de cadastro da pessoa física (CPF), nome completo e data de nascimento de um cidadão.
Concluímos que um dado é formado por um registro mais um estado deste registro. Logo, o conceito de dados é contável, ou seja, um dado pode ser aglomerados em um conjunto de dados para representação da informação. Desta maneira é possível relacionar outros tipos de informação aos registros binários, concatenando diversos registros e seus respectivos estados, figura 03.
Figura 03 – As palavras em um painel de LED são formadas pelos estados de seus LEDs constituintes.
Fonte: casas bahia
Uma vez que um dado é contável ele deve possuir uma unidade. A unidade utilizada em computação para a contagem de dados é o BIT. Um BIT equivale a um registro binário com um estado.
1 BIT = REGISTRO + ESTADO
Logo, quando falamos de dados podemos citar sua quantidade como, por exemplo: 40 BITs de dados sobre algo ou alguma coisa, ou seja, 40 registros binários, cada um com seu estado.
Em computação é comum utilizarmos 8 BITs, agrupá-los e definir uma nova unidade chamada de BYTE.
8 BIT = 1 BYTE
A partir do BYTE podemos definir diversas outras unidades, tabela 01.
Tabela 01 – Múltiplos do BYTE no S.I (Base 10).
| Unidade | Sigla | Valor |
|---|---|---|
| 1 BYTE | 1 B | $ 10^1 $ |
| 1 KILOBYTE | 1 KB | $ 10^3 $ |
| 1 MEGABYTE | 1 MB | $ 10^6 $ |
| 1 GIGABYTE | 1 GB | $ 10^9 $ |
| 1 TERABYTE | 1 TB | $ 10^{12} $ |
| 1 PETABYTE | 1 PB | $ 10^{15} $ |
| 1 EXABYTE | 1 EB | $ 10^{18} $ |
| 1 ZETTABYTE | 1 ZB | $ 10^{21} $ |
| 1 YOTTABYTE | 1 YB | $ 10^{24} $ |
Fonte: Autor.
Definidas as unidades quantitativas dos dados e os preceitos físicos que os constituem algumas perguntas interessantes sobre sua presença e dimensionamento podem ser exploradas, estudas e respondidas (Figura 04):
Quantos dados são criados na internet por dia?
463 EB = 463.000.000.000.000.000.000 BYTES.
Quantos dados existem no universo digital?
44 ZB = 44.000.000.000.000.000.000.000 BYTES.
Figura 04 – “A Day in Data” estima a produção de 463 EB de dados por dia.
Fonte: raconteur.
Essa quantidade de dados necessita de uma quantidade equivalente de registros. Este fato inspira reflexão quanto ao tratamento do problema de armazenamento e processamento de toda essa informação.
Processamento de dados
Quando a quantidade de dados é significativa um programa pode demorar para resolver o problema proposto ou precisar de muita memória para trata-ló, ou seja, necessitar de muito recurso computacional. Nesse contexto, a qualidade dos programas propostos para uma determinada solução impacta a possibilidade de implementá-lo, utilizá-lo, ou ambos, ou seja, o processamento de dados requer o tratamento ótimo da informação.
Existem algumas soluções para avaliar a qualidade dos programas, além de sua funcionalidade. Estas soluções são baseadas nas operações sobre os dados como, por exemplo:
- Acessar;
- Comparar;
- Modificar;
- Transferir.
Saber como computar a quantidade de dados é como saberemos o quão eficiente é o número de operações sobre uma quantidade de dados que um programa necessita realizar para resolver um problema proposto.
No que tange a ciência, a computação de uma quantidade grande de dados (big data) representou a criação de um novo paradigma (4° paradigma) sendo concebido um novo método de avançar as fronteiras do conhecimento, por meio de novas tecnologias para coletar, manipular, analisar e exibir dados, construindo valor agregado com as análises geradas.
Representação de dados
Nem todo tido tipo de informação pode ser representada por um registro binário (“0” e “1”). Em muitas situações é útil representar os dados de outras natureza como, por exemplo, o número de cadastro da pessoa física (CPF), nome completo e data de nascimento de um cidadão.
Podemos relacionar este tipo de informação com um registro binário por meio de um conjunto de registros binários que, quando combinados, representam uma abstração para a representação destes dados.
As letras do alfabeto podem ser representadas por um conjunto de registros binários:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
| reg. 1 | reg. 2 | reg. 3 | reg. 4 | reg. 5 | reg. 6 | reg. 7 | reg. 8 | . . . | reg. N |
Onde cada uma das letras do alfabeto pode ser representada por um conjunto de estados de 8 registros binários, ou seja, 1 BYTE:
A equivale a $ {(01000001)}_2 $
Observemos que podemos utilizar dos mesmos registros, e na mesma ordem, para representar cada letra:
| Letra | reg. 1 | reg. 2 | reg. 3 | reg. 4 | reg. 5 | reg. 6 | reg. 7 | reg. 8 |
|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| B | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
Este tipo de codificação entre um conjunto de registros e uma possibilidade de estado é bastante comum. Normalmente existem tabelas que associam os registros com alguma possibilidade de estado como, por exemplo, a tabela ASCII (Tabela 02).
Tabela 02 – A tabela ASCII é uma tabela padrão de comunicação americana para a troca de informação.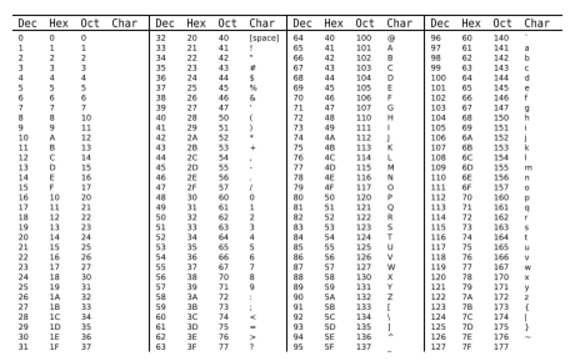
Fonte: pngegg.
Sabendo que existem dados que possuem mais possibilidades de estados do que as duas possibilidades de um registros binário, podemos observar que estes dados necessitam de um número de registros binários maior do que 1 para serem representados. Logo, existe uma relação entre o tipo de dado e o tamanho (quantidade de registros binários) de um dado.
Assim, cada tipo de dado tem um tamanho, equivalente ao número de registros binários necessários para representar todos os estados possíveis. O tamanho de um tipo de um dados é representado por BITs ou BYTEs. (Tabela 04)
Sabemos que para cada registro binário temos:
$ 2 $ possibilidades de estado
e para cada registro binário adicionado ao registro, o número destas possibilidades será dobrada:
$ 2.2.2.2.2 \cdots n $ possibilidades de estado
Assim, para saber o número de estados (x) que um número de BITs (n) pode representar fazemos:
$ x = 2^n $
Analogamente, o número de bits necessários para representar uma quantidade de dados é calculado por:
$ n = log_{2} x $
Tabela 03 – Tipos de dados na linguagem C.
| Tipo | Tamanho | Qtd. de Estados | Valores Possíveis |
|---|---|---|---|
| boolean | 1 bit | $ 2^1 $ | true e false |
| byte | 1 byte | $ 2^8-1 $ | $ -127 $ à $ 128 $ |
| short int | 2 bytes | $ 2^{16}-1 $ | -32768 à 32767 |
| int | 4 bytes | $ 2^{32}-1 $ | -2147483648 à 2147483647 |
| long int | 8 bytes | $ 2^{64}-1 $ | -9223372036854775808 à 9223372036854775807 |
| float | 4 bytes | $ 2^{32}-1 $ | $ 3,4 \cdot 10^{-38} $ à $ 3,4 \cdot 10^{38} $ |
| double | 8 bytes | $ 2^{64}-1 $ | $ 1,7 \cdot 10^{-308} $ à $ 1,7 \cdot 10^{308} $ |
| char | 1 byte | $ 2^8-1 $ | 0 a 255 |
Fonte: Autor.
Referências
- A day in Data. Disponível em: <https://www.raconteur.net/infographics/a-day-in-data/>. Acesso em: 05/02/2021.
- PIVA JÚNIOR, Dilermando (et al). Estrutura de dados e técnicas de programação. 1. ed. Rio de Janeiro, RJ: Campus, 2014. 399 p. ISBN: 9788535274370.
- CORMEN, Thomas H et al. Algoritmos: teoria e prática. Rio de Janeiro: Elsevier, 926 p. ISBN: 9788535236996.
- TOSCANI, Laira Vieira; VELOSO, Paulo A. S. Complexidade de algoritmos: análise, projeto e métodos. 3. ed. Porto Alegre: Bookman, 2012. 261 p. (Série livros didáticos informática UFRGS, 13) ISBN: 9788540701380.
- ASCENCIO, Ana Fernanda Gomes. Estruturas de dados: algoritmos, análise da complexidade e implementações em Java e C/C++. São Paulo: Pearson, c2010. 432 p. ISBN: 9788576052216, 978857605816.
- Hey, Tony; Tansley, Stewart; Tolle, Kristin (1 de outubro de 2009). The Fourth Paradigm: Data-Intensive Scientific Discovery. Microsoft Research (em inglês).
- BRASSARD, Gilles; BRATLEY, Paul. Fundamentals of algorithmics. Englewood Cliffs: Prentice Hall, c1996. xx, 524 p. ISBN: 0133350681.
Livraria
