O Problema de Fluxo de Carga é o estudo de sistemas elétricos de potência (SEP) em regime permanente para uma condição de carga e de geração. Este estudo demanda uma análise numérica extensa. Contudo, trata-se de um problema matemático formado por um conjunto de equações fasoriais cuja solução determina os valores de tensão nas barras.
Com os valores das tensões nas barras e os parâmetros do sistema calculam-se a potência líquida nas barras, as correntes nas linhas, o carregamento dos transformadores, as perdas ativas e o balanço de reativos do sistema em estudo.
Objetivamente, o problema de fluxo de carga consiste na obtenção das condições de uma rede elétrica (Figura 01) em função de sua topologia e dos níveis de carga e de geração de potência.
No cálculo do fluxo de carga as grandezas do sistema de potência são representadas em sistemas por unidade, que facilita o cálculo para sistemas com mais de um nível de tensão.
Figura 01 – Sistema IEEE 30 barras-Modelagem da Rede Elétrica no Nível Barra-Ramo.

Fonte: https://www.researchgate.net/figure/Figura-2-Sistema-IEEE-30-barras-Modelagem-da-Rede-Eletrica-no-Nivel-Barra-Ramo_fig2_262745037
Diretrizes iniciais para o estudo:
- Diagrama unifilar do sistema: dados para o estudo matricial e computacional;
- Dados das linhas, dos transformadores e das barras;
- Matriz admitância de barra $ \left [ Y_{barra} \right ] $: uso das admitâncias próprias $Y_{kk}$ e mútuas $Y_{kn}$ da matriz;
- A potência gerada e consumida em cada barra;
- As potências ativa e reativa líquida nas barras $ ( P_{líquida} = P_{gerador}-P_{carga} $ e $ Q_{líquida} = Q_{gerador}-Q_{carga} ) $;
- Grandezas representadas em sistemas por unidade;
- São definidas barras especiais para o estudo conforme a tabela 01.
Tabela 01 – Tipos de barras de um sistema elétrico.
| Tipo | Grandezas Especificadas | Grandezas à Determinar |
|---|---|---|
| Barra Slack ou Barra de balanço |
$ P_{carga} $ e $ Q_{carga} $ $ \left | V \right | $ e $ \delta $, usualmente $ V=1\angle 0^{\circ} $ pu |
$ P_{líquida} $ e $ Q_{líquida} $ |
| Barra PQ ou Barra de Carga |
$ P_{líquida} $ e $ Q_{líquida} $ | $ \left | V \right | $ e $ \delta $ |
| Barra PV ou Barra de Tensão Controlada |
$ P_{líquida} $ e $ \left | V \right | $ | $ Q_{líquida} $ e $ \delta $ |
Fonte: Autor.
*Convencionalmente, a potência aparente absorvida por uma carga é uma entrada negativa de potência.
No estudo de fluxo de carga existem três tipos de barras: a barra de balanço (Slack), a barra de tensão (PV) e a barra de carga (PQ).
A barra de balanço (Slack) tem como função manter o balanço de potências de um sistema, ou seja, atuará no equilíbrio do balanço entre as potências geradas e consumidas de um sistema. Supondo um sistema com 3 geradores, após o fluxo de carga convergido a soma da potência gerada em cada gerador devera ser igual a soma das potências consumidas em cada barra do sistema mais as perdas. Considerando que a geração pode ser despachável podem existir várias combinações de modo a suprir a potência consumida pelo sistema. Se o sistema gerar mais potência que a consumida a barra Slack absorverá essa potência, caso contrário, ela irá provê a potência para suprir as cargas e perdas do sistema.
As barras de carga (PQ) são aquelas em que se especifica a potência ativa e reativa de carga na barra. A maioria das barras de um sistema de potência são barras de carga (PQ), especialmente as de baixa tensão.
As barras de tensão controlada (PV) são aquelas em que se preserva a magnitude da tensão em um valor especificado através de um sistema de controle de tensão por meio da injeção de reativo. Além disso, a potência líquida na barra será a diferença entra as potências gerada e a consumida na barra.
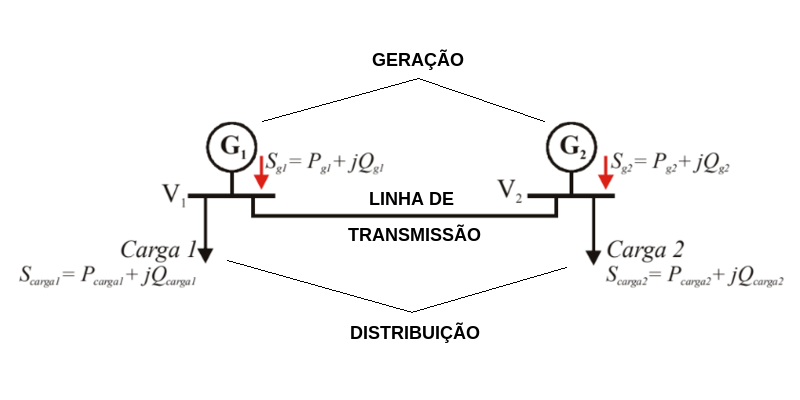
Consideremos a corrente total que entra no barramento $ k $ de um sistema genérico de barramento n (Figura 02).
Figura 02 – Sistema com duas barras e seu circuito equivalente com injeção de corrente.

Fonte: ELGERD, O. I., Introdução à Teoria de Sistemas de Energia Elétrica, McGraw-Hill, São Paulo-SP, 1981.
Pelo método de análise nodal de circuitos elétricos, baseado na 1ª Lei de Kirchhoff, a formulação geral para um sistema com N barras é:
| $ \begin{bmatrix} I_{1} \\ I_{2} \\ \vdots \\ I_{k} \end{bmatrix}=\begin{bmatrix} Y_{11} & Y_{12} & \cdots & Y_{1N} \\ Y_{21} & Y_{22} & \cdots & Y_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ Y_{N1} & Y_{N2} & \cdots & Y_{NN} \end{bmatrix} \begin{bmatrix} V_{1} \\ V_{2} \\ \vdots \\ V_{n} \end{bmatrix} $ | (1) |
a qual pode ser rescrita na sua forma compacta como:
| $ \left [ I \right ] = \left [ Y_{barra} \right ] \left [ V \right ] $ | (2) |
logo, a k-ésima injeção de corrente no nó $ k $ é dada por:
| $ \displaystyle I_{k}=\sum_{n=1}^{N}Y_{kn}V_{n} $ | (3) |
a qual pode ser rescrita de forma a representar suas componentes próprias e mútuas do nó como:
| $ \displaystyle I_{k}=Y_{kk}V_{k}+\sum_{\substack{ n=1 \\ n \neq k }}^{N}Y_{kn}V_{n} $ | (4) |
onde:
- $ Y_{kk} $ é a admitância própria, formada pela soma das admitâncias conectadas a barra $ k $;
- $ Y_{kn} $ é a admitância mútua conectadas a barra $ k $.
Resolvendo para a tensão no nó $ k $, $ V_k $, obtém-se:
| $ \displaystyle V_{k}=\dfrac{1}{Y_{kk}} \left ( I_{k}-\sum_{\substack{ n=1 \\ n \neq k }}^{N}Y_{kn}V_{n} \right ) $ | (5) |
A potência $ S_k $ (diferença entre as potências do gerador e da carga na barra $ k $) é conhecida como Potência da Barra. Pode ser considerada como injetada na barra por uma “fonte de potência de barra”, Figura 02.
Para determinar as correntes injetadas em cada nó, considere em primeiro lugar a potência aparente injetada na barra $ k $, $ S_k = P_k + jQ_k $, dada por:
| $ S_k = S_{k_{gerador}}-S_{k_{carga}} $ | (6) |
onde:
| $ P_k = P_{k_{gerador}}-P_{k_{carga}} $ | (7) |
| $ Q_k = Q_{k_{gerador}}-Q_{k_{carga}} $ | (8) |
Assim, a corrente injetada na barra $ k $ é expressa como:
| $ \displaystyle S_k=V_k I_k^* \Rightarrow I_k=\dfrac{P_k-jQ_k}{V_k^*} $ | (9) |
Finalmente, com as equações (5) e (9), para um sistema com $ N $ barras, obtém-se as equações não lineares de fluxo de potência para o método de Gauss-Seidel:
| $ \displaystyle V_{k}=\frac{1}{Y_{kk}} \left ( \dfrac{P_k-jQ_k}{ \displaystyle V_k^*}-\sum_{\substack{ n=1 \\ n \neq k }}^{N}Y_{kn}V_{n} \right ) $ para $ k=2,3,\cdots,N $ | (10) |
As mesmas equações rescritas para o método Newton-Raphson:
| $ \displaystyle P_k-jQ_k=\sum_{n=1}^{N}{ \left [ V_kV_ne^{(\delta_n-\delta_k)} \left ( G_{kn}+jB_{kn} \right ) \right ] } $ para $ k=2,3,\cdots,N $ | (11) |
Como o sistema possui $ N $ barras, teremos $ N $ equações. Porém, como temos o valor de tensão da barra Slack, não necessitamos calcular a tensão dela e o sistema de interesse passa a ser um conjunto de $ N-1 $ equações pra o fluxo de potência, ou seja, não é necessária uma equação para a barra $ 1 $ ($ k $ começa a partir de $ 2 $) pois esta foi adotada como a barra slack.
A maioria dos procedimentos de solução numérica de modelos envolvendo sistemas de equações não lineares envolve, no seu cerne, a solução de sistemas lineares. Assim, este conjunto de equações é resolvido por métodos computacionais iterativos (Gauss, Gauss-Seidel, Newton Raphson, Newton Desacoplado, Newton Desacoplado rápido etc) para que se obtenha os valores das tensões de barra.
Valores iniciais são arbitrados de forma conveniente às equações:
- As barras de carga (PQ): $ {\left | V \right |}^{(0)} $ e $ \delta^{(0)} $
- As barras de tensão controlada (PV): $ \delta^{(0)} $
- Na prática como a variação de tensão não é muito grande, costuma-se atribuir valores iniciais para as tensões desconhecidas iguais ou próximos ao da barra slack, ou seja, em torno de 1,0 p.u para as magnitudes e de $ 0^{\circ} $ para os ângulos.
Diagrama do fluxo de carga por Gauss-Seidel:
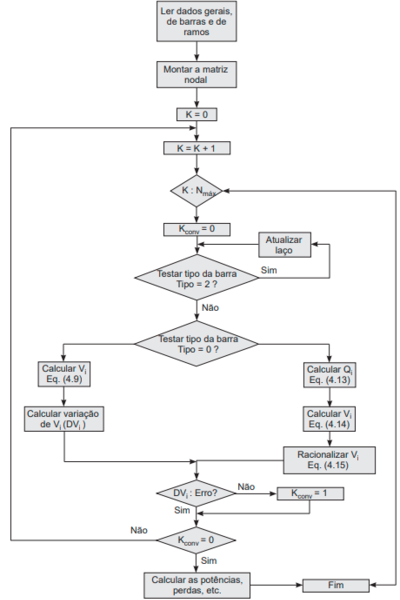
Algoritmo de fluxo de carga por Gauss-Seidel, em scilab:
A correta implementação da solução para o problema de fluxo de carga serve como base para a garantia da qualidade, confiabilidade e da segurança operacional dos SEP.
Existe um grande conjunto de aplicações para a solução do problema do fluxo de carga, tais como:
- Análise de contingência: o fluxo de carga é usado para analisar cada contingência da rede elétrica, ou seja, a análise de cada possibilidade de que alguma coisa aconteça ou não como, por exemplo, o comissionamento ou descomissionamento de algum equipamento na rede elétrica de potência;
- Confiabilidade: sabendo dos dados probabilísticos de falha dos diversos componentes da rede, é possível estimar a probabilidade de falha de suprimento ao consumidor a fim de torná-la menor que um percentual (indicador) especificado através de investimento no sistema. Para tal, o fluxo de carga é utilizado para verificar a adequação de cada estado com falha do sistema simulado;
- Curto-circuito: cálculo das tensões pré-falta;
- Fluxo de carga ótimo: este estudo fornece a melhor topologia/configuração para minimizar o custo de operação ou minimizar as perdas. É um fluxo de potência com as restrições de um problema de otimização combinatória.
Referências
- Notas de aula do prof. Dr. Max Chianca Pimentel Filho;
- ELGERD, O. I., Introdução à Teoria de Sistemas de Energia Elétrica, McGraw-Hill, São Paulo-SP, 1981;
- J. J. Grainger and W.D. Stevenson Jr. Power Systems Analysis, McGraw-Hill, 1994.
- J. D. Glover, M. S. Sarma and T. J. Overbye. Power Systems Analysis and Design, 4th Edition – Thomson, 2008.
- A. R. Bergen and V. Vittal. Power Systems Analysis, 2nd Edition, Prentice Hall, 2000.
- Prabha Kundur, Power System Stability and Control, McGraw-Hill, 1994.
- GÓMEZ-EXPÓSITO, A., CONJETO, A. J., CAÑIZARES, C., Sistemas de Energia Elétrica – Análise e Operação, LTC, Rio de Janeiro, 2011.
