Os principais fatores que determinam a resistividade do solo são:
- Tipo do solo;
- Composição química e concentração de sais contidos no solo;
- Umidade do solo;
- Granulometria do material que compõe o solo e a sua distribuição;
- Composição do solo.
O tipo do solo é muito importante na determinação do valor da resistividade, mas o valor da resistividade dos diversos tipos de solo não é claramente definido. Sendo assim, a partir de medições, pode-se estabelecer faixas de variação de resistividade por tipo de solo. Veja a seguinte tabela.
| Tipo de solo | Resistividade $ \left( \Omega \cdot m \right) $ |
| solos alagadiços, limo, humo, lama | até 150 |
| solos aráveis, argilo-arenoso | 50 a 500 |
| argila | 300 a 5.000 |
| areia | 1.000 a 8.000 |
| calcáreo | 500 a 5.000 |
| granito arenito | 100 a 10.000 |
| basalto | 10.000 a 20.000 |
Os métodos tradicionais de medição da resistividade do solo envolvem a injeção de uma corrente conhecida no solo e a medição da diferença de potencial ou intensidade de campo elétrico resultante. Estão enquadrados nesses procedimentos respectivamente os métodos de Wenner e de Schlumberger.
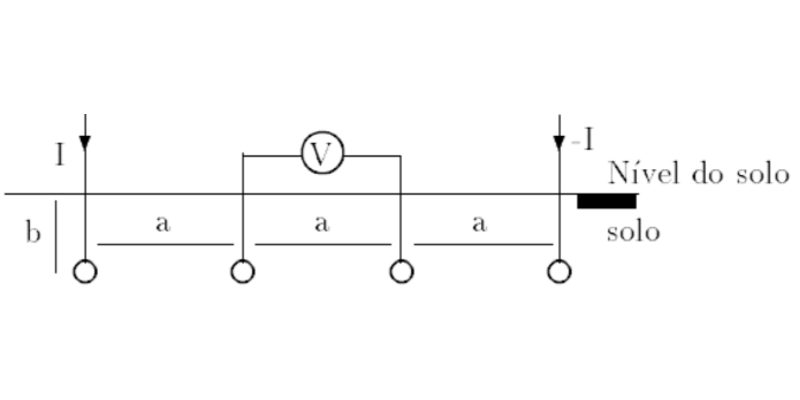
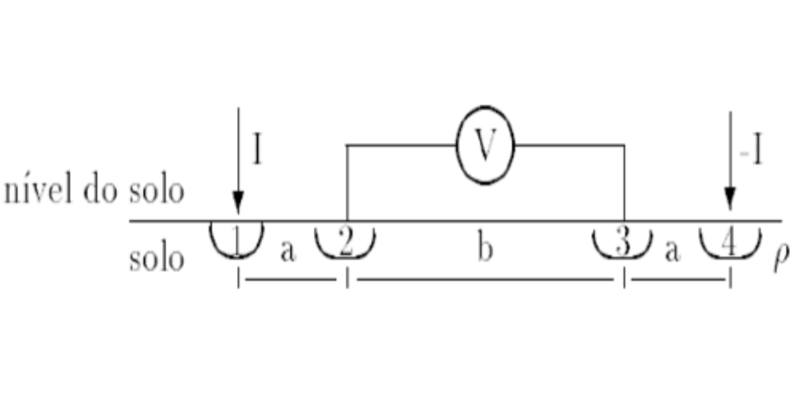
Nos métodos de Wenner e de Schlumberger, a resistividade do solo é considerada uniforme. Sabe-se na realidade que isto não acontece. O solo é composto de várias camadas de resistividade diferentes e que nas camadas mais profundas, a diferença de valores entre uma camada e outra é pequena, podendo ter-se valores constantes. A partir daí pode ser considerada homogênea e de profundidade infinita, tendo em vista que a corrente dispersa nesta camada não influencia nos potenciais da superfície do solo ou em pontos logo abaixo.
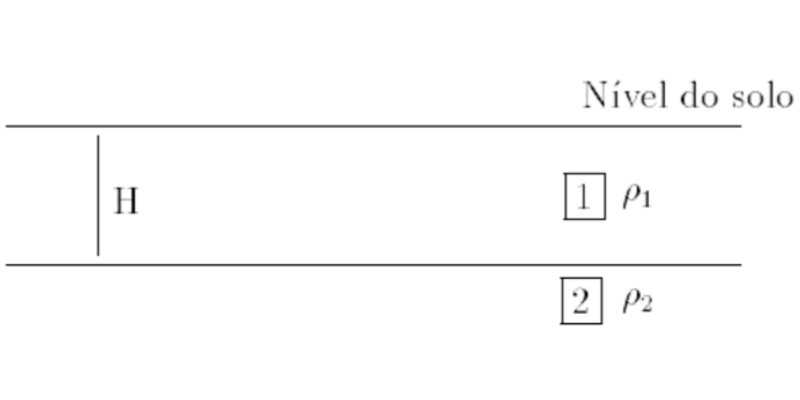
A maioria dos solos podem ser bem representada, tomando-se um modelo equivalente composto por duas camadas, conforme figura abaixo.
Considere um solo com esta estrutura. Suponhamos 4 eletrodos semi esféricos espaçados igualmente na superfície do solo, conforme a figura abaixo.
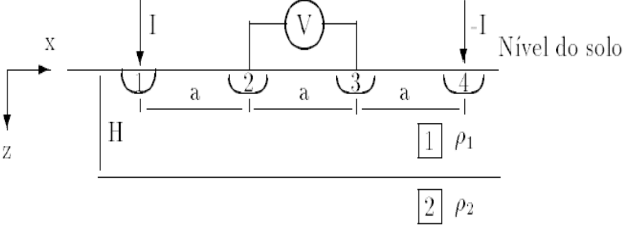
Sabe-se que o potencial no meio $ 1 $ devido uma fonte pontual injetando corrente $ I $ neste meio, é dada por
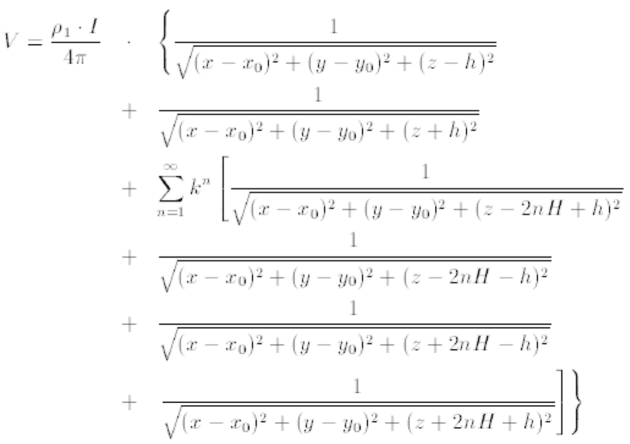
Considere apenas duas dimensões, $ x $ e $ z $, e suponha duas fontes pontuais injetando corrente $ I $ e $ -I $ nos pontos de coordenadas:
$ \displaystyle I \rightarrow \lbrace x_0=0, h=0 \rbrace $
$ \displaystyle -I \rightarrow \lbrace x_0=3a, h=0 \rbrace $
Os potenciais nos pontos 2, $ \left( x=a, z=0 \right) $, e $ 3 $, $ \left( x=2a, z=0 \right) $, devido as correntes $ I $ e $ -I $ são

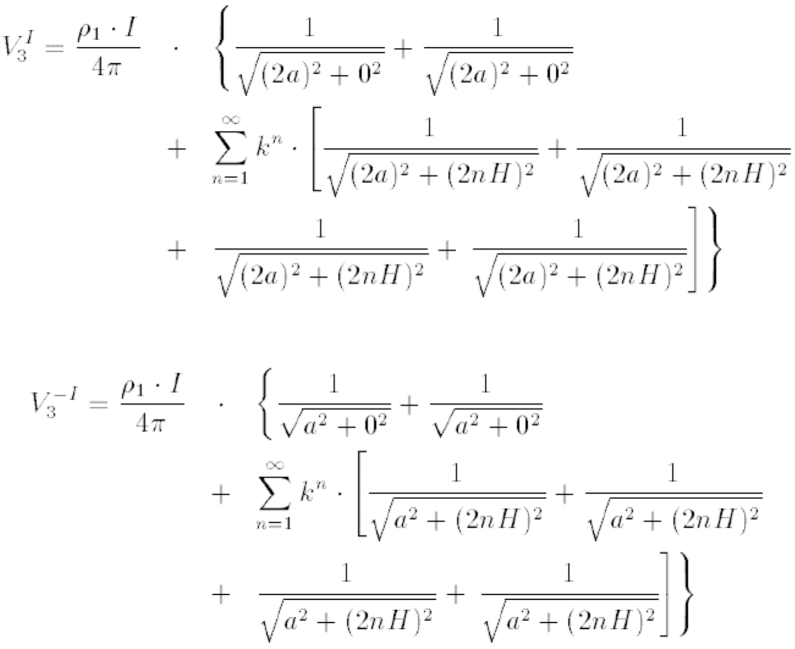
Simplificando as expressões, teremos
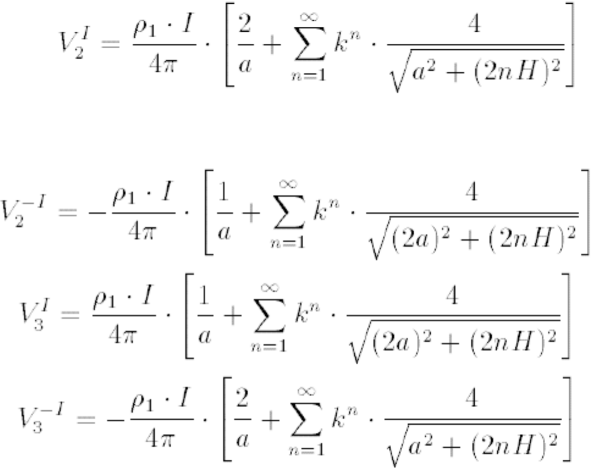
Os potenciais nos pontos $ 2 $ e $ 3 $ são dados pela soma dos potenciais $ V_2^{I} $ e $ V_2^{-I} $ e, $ V_3^{I} $ e $ V_3^{-I} $. Assim sendo, $ V_{23} $ é dado por
$ \displaystyle V_{23} = V_2-V_3 = \left( V_2^{I}+V_2^{-I} \right) – \left( V_3^{I}+V_3^{-I} \right) $
Logo,
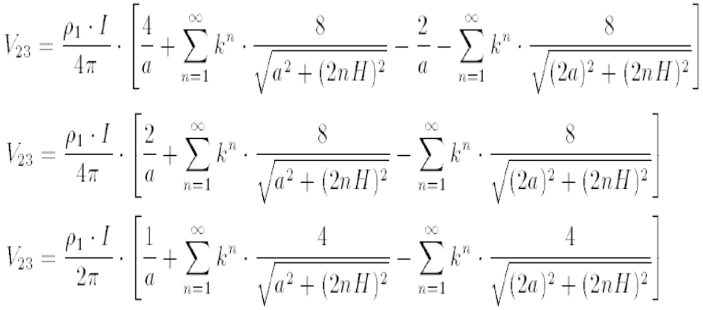
A resistência mútua entre $ 2 $ e $ 3 $, é
$ \displaystyle R = \frac{V_{23}}{I} = \frac{\rho_1}{2\pi} \cdot \left[ \frac{1}{a} + \sum_{n=1}^\infty{k^n\cdot\frac{4}{\sqrt{a^2+\left(2nH\right)}^2}}-\sum_{n=1}^\infty{k^n\cdot\frac{4}{\sqrt{\left(2a\right)^2+\left(2nH\right)}^2}} \right] $
Tem-se do método de Wenner (quando considera-se o espaçamento entre eletrodos muito maior que a profundidade) que a resistividade é dada por
$ \displaystyle \rho = 2 \cdot \pi \cdot a \cdot R $
Expressão idêntica à expressão obtida de eletrodos semi-esféricos injetando corrente num solo de resistividade homogênea $ \rho $, relacionando
$ \displaystyle R = \frac{\rho}{2 \pi a} $
com a expressão anteriormente deduzida, teremos
$\displaystyle \frac{\rho}{2 \pi a} = \frac{\rho_1}{2 \pi a} \left\{ 1 + 4 \cdot \sum_{n=1}^\infty{ k^n \cdot \left[ \frac{1}{\sqrt{1+{ \left( \frac{2nH}{a} \right) }^2}}-\frac{1}{\sqrt{4+{ \left( \frac{2nH}{a} \right) }^2}} \right] } \right\} $
$ \displaystyle \frac{\rho}{\rho_1} = 1 + 4 \cdot \sum_{n=1}^\infty{ k^n \cdot \left[ \frac{1}{\sqrt{1+{\left(\frac{2nH}{a}\right)}^2}}-\frac{1}{\sqrt{4+{\left(\frac{2nH}{a}\right)}^2}} \right] } $
Referências
- TELLÓ, Marcos (Org). Aterramento elétrico impulsivo, em baixa e alta frequências: com apresentação de casos. Porto Alegre: EdiPUCRS, 2007. 328 p. ISBN: 9788574306230.
- ZANETTA JÚNIOR, Luiz Cera. Transitórios eletromagnéticos em sistemas de potência. São Paulo: EDUSP, 2003. 712 p. (Acadêmica, n.52) ISBN: 8531407559.