Dado o sistema elétrico interligado regional representado na figura abaixo:
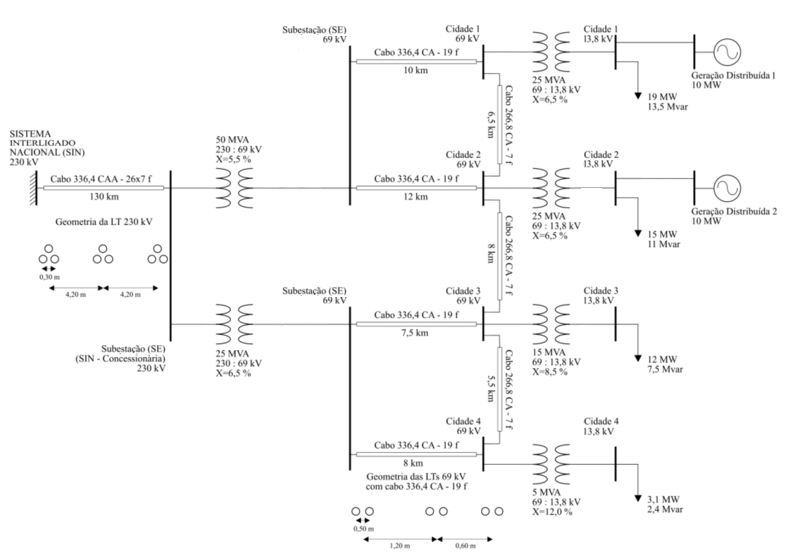
Deve-se atentar aos elementos, aos tipos de barras e as zonas de operação presentes no sistema:

No ANAREDE, os parâmetros elétricos de operação devem estar representados em sistemas por unidade.
Destacados os elementos, os tipos de barras e as zonas de operação do sistema é possível definir suas bases de operação e quantificar e modelar as características dos elementos (geradores, linhas de transmissão, transformadores etc) que os constituem.
Zonas de Operação do Sistema
As zonas de operação do sistema são definidas por:
| Zona de operação |
Potência Aparente de Base [MVA] |
Tensão Elétrica de Base [kV] |
Impedância Elétrica de Base [ $ \Omega $ ] |
|---|---|---|---|
| 0 | 100 | 230 | 529 |
| 1 | 100 | 69 | 47,61 |
| 2 | 100 | 13,8 | 1,90 |
Modelagem das Barras
O ANAREDE permite a modelagem de 4 tipos de barras CA:
- 0 – PQ: Barra PQ;
- 1 – PV: Barra PV;
- 2 – Referência: Barra de Balanço ou Referência;
- 3 – PQ VLIM: Barra PQ com controle de módulo de tensão.
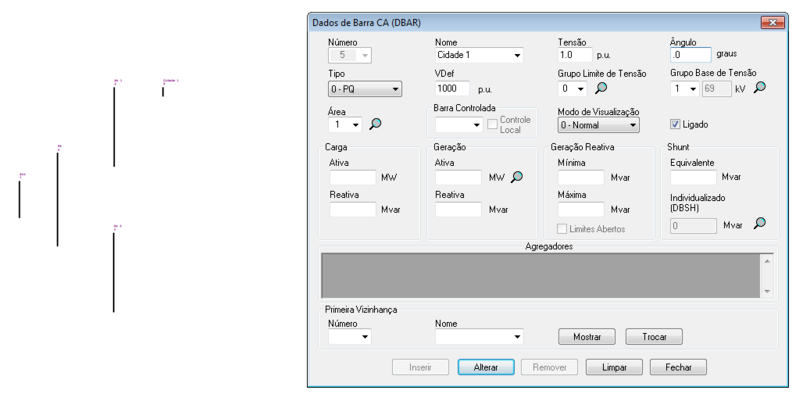
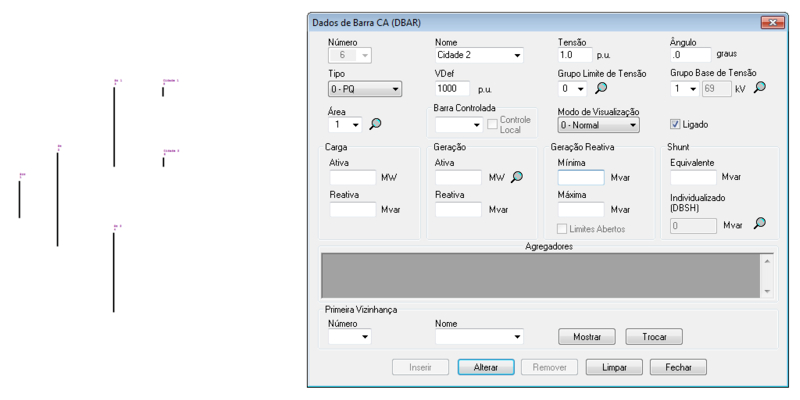
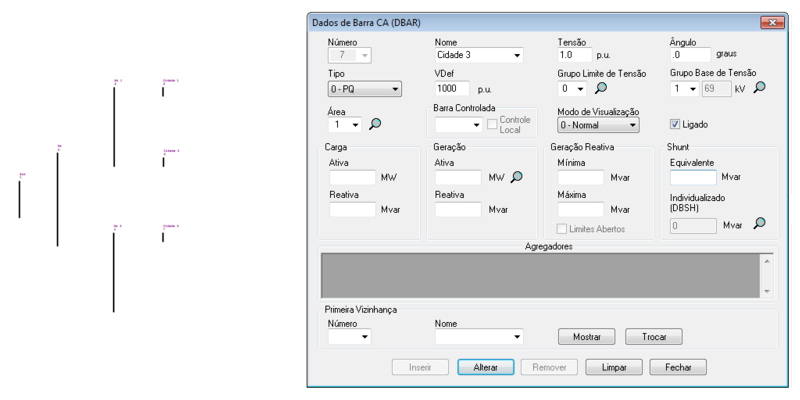
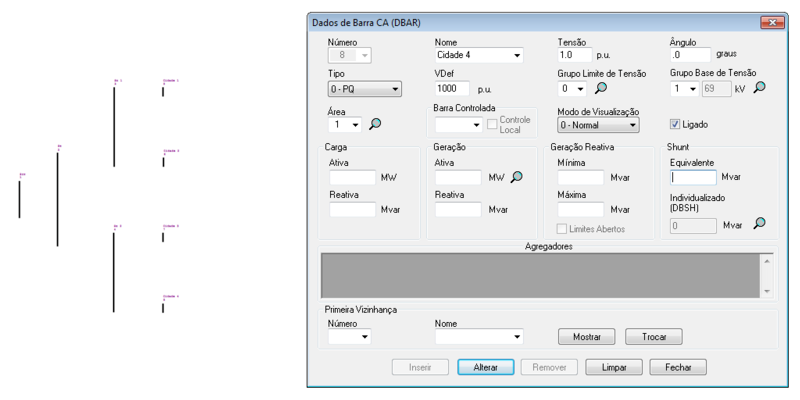
As barras para o sistema podem ser sintetizadas em:
| Barra | Zona de operação |
Tipo | Módulo da tensão elétrica (p.u) |
Fase da tensão elétrica ( \circ ) |
Potência ativa do gerador [MVA] |
Potência reativa do gerador [MVAr] |
Potência ativa da carga [MVA] |
Potência reativa da carga [MVAr] |
|---|---|---|---|---|---|---|---|---|
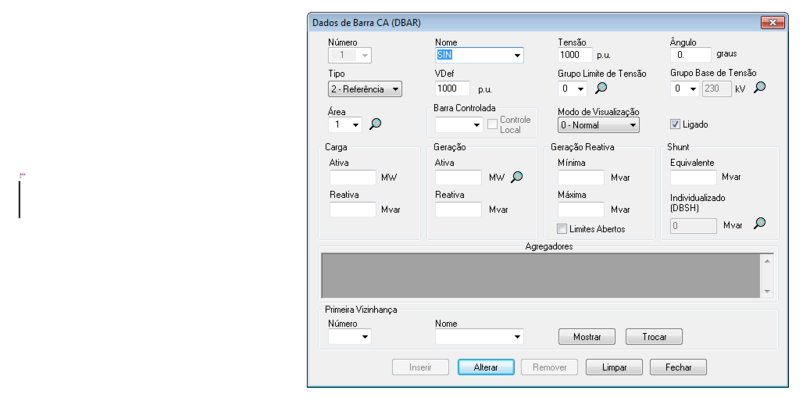
| 01 | 0 | 2 | 1,00 | 0 | 0 | 0 | 0 | 0 |
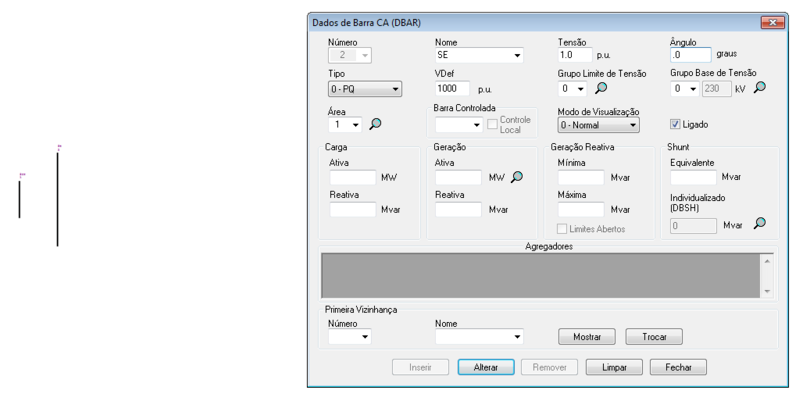
| 02 | 1 | 0 | 1,00 | 0 | 0 | 0 | 0 | 0 |
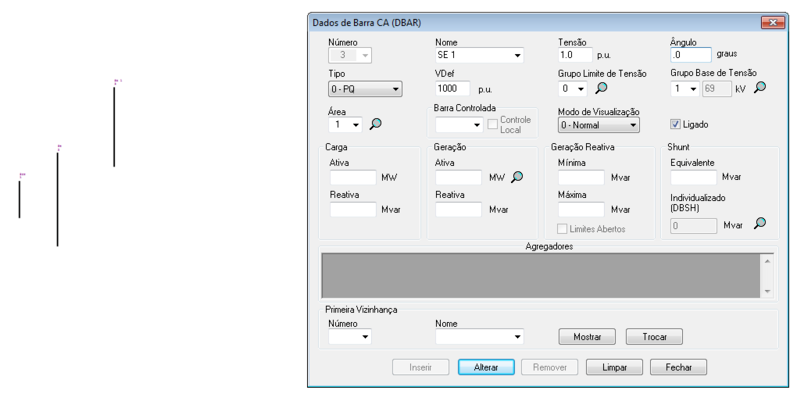
| 03 | 1 | 0 | 1,00 | 0 | 0 | 0 | 0 | 0 |
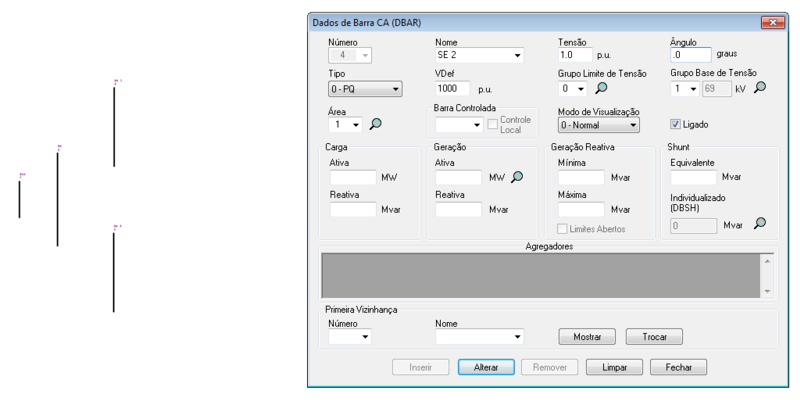
| 04 | 1 | 0 | 1,00 | 0 | 0 | 0 | 0 | 0 |
| 05 | 1 | 0 | 1,00 | 0 | 0 | 0 | 0 | 0 |
| 06 | 1 | 0 | 1,00 | 0 | 0 | 0 | 0 | 0 |
| 07 | 1 | 0 | 1,00 | 0 | 0 | 0 | 0 | 0 |
| 08 | 1 | 0 | 1,00 | 0 | 0 | 0 | 0 | 0 |
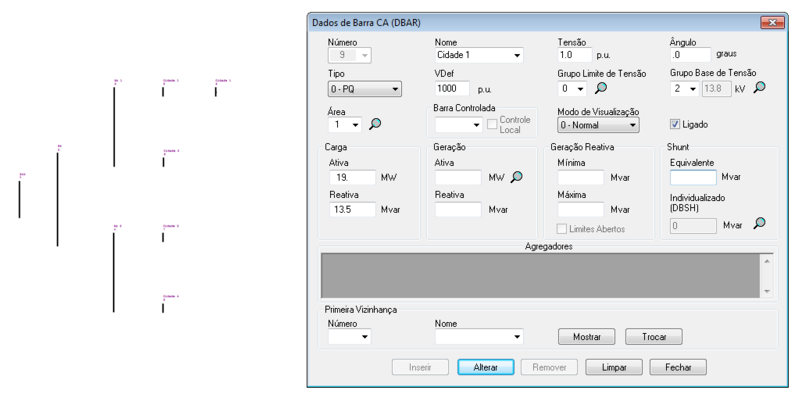
| 09 | 1 | 0 | 1,00 | 0 | 10,0 | 0 | 19,0 | 13,5 |
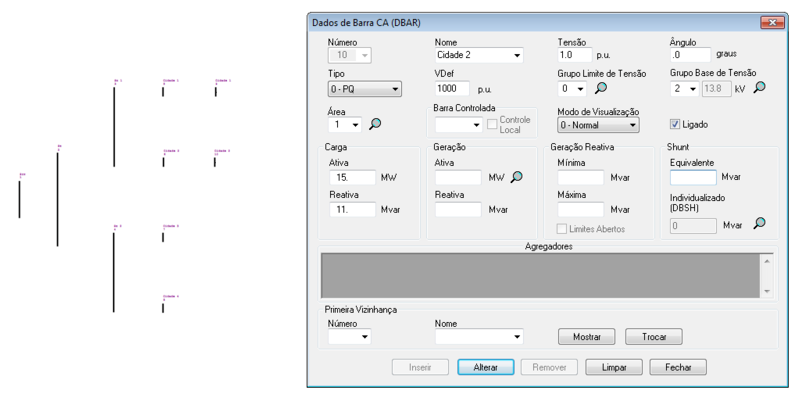
| 10 | 1 | 0 | 1,00 | 0 | 10,0 | 0 | 15,0 | 11,0 |
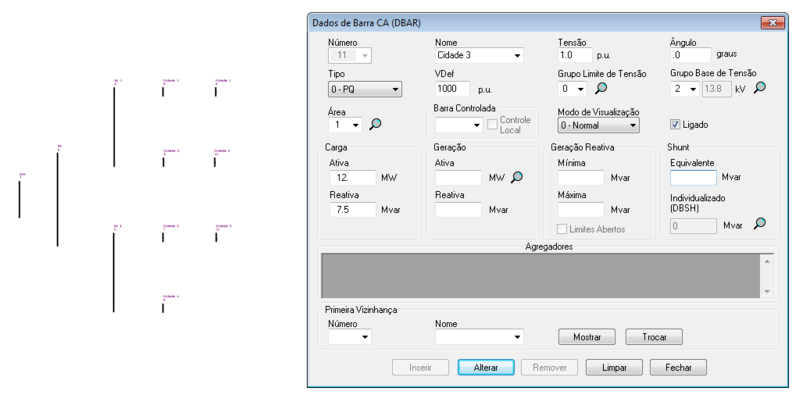
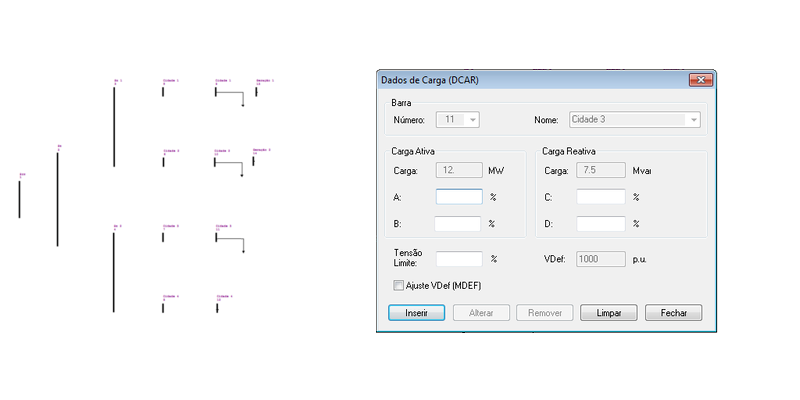
| 11 | 1 | 0 | 1,00 | 0 | 0 | 0 | 12,0 | 7,50 |
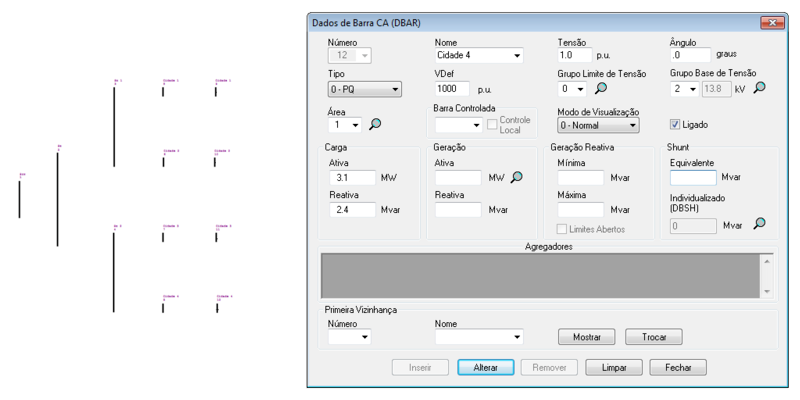
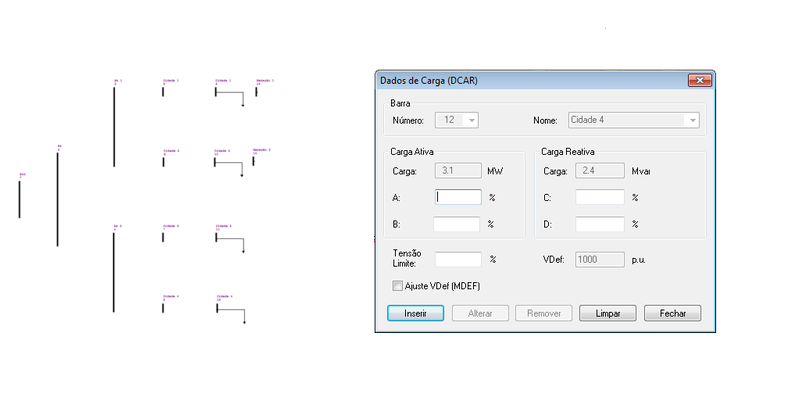
| 12 | 1 | 0 | 1,00 | 0 | 0 | 0 | 3,10 | 2,40 |
O ANAREDE permite a representação das barras no diagrama do sistema, tal como:
Modelagem das Cargas e Geradores
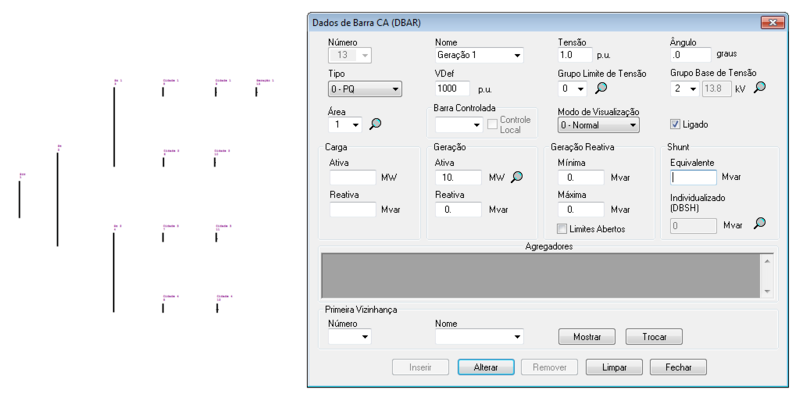
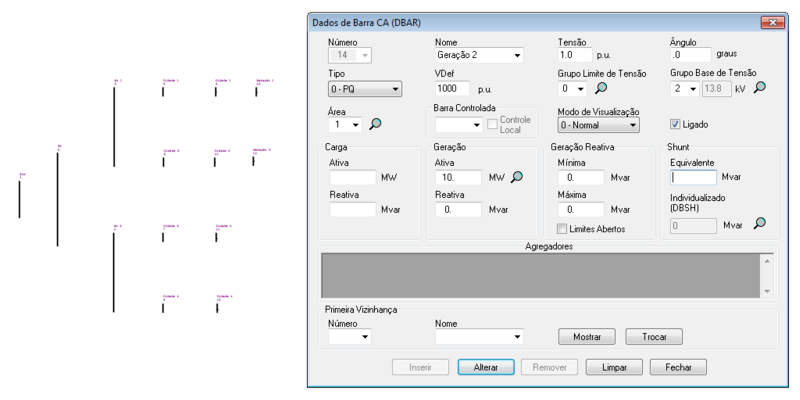
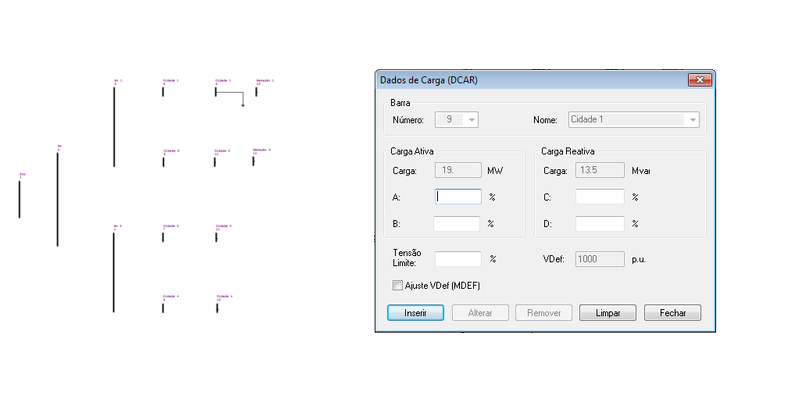
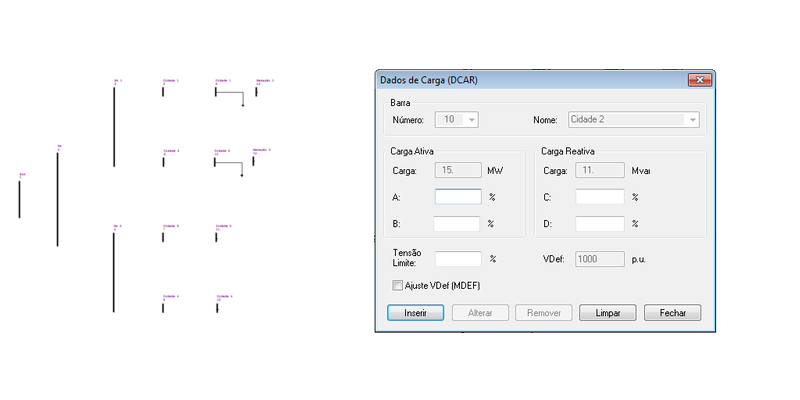
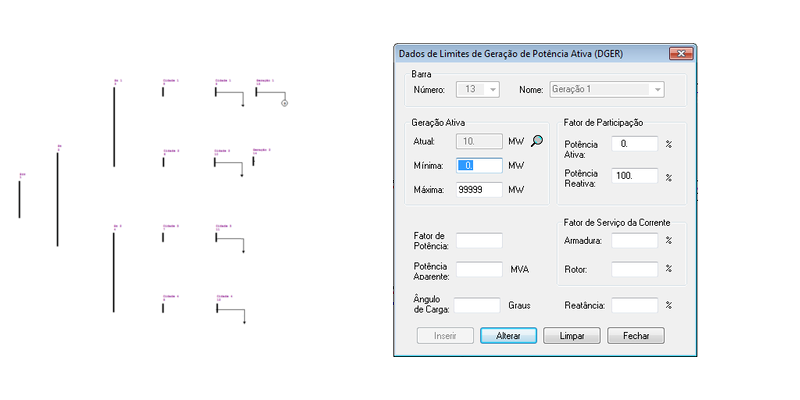
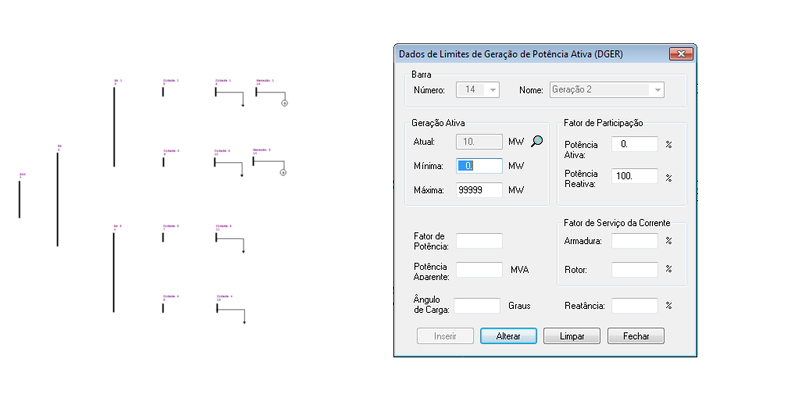
O ANAREDE permite a representação das cargas e dos geradores inseridos nas barras no diagrama do sistema, tal como:
Modelagem dos Transformadores
Os fabricantes dos transformadores fornecem apenas um valor em p.u para a impedância dos transformadores pois o valor referido ao lado de alta tensão é igual ao valor referido ao lado de baixa tensão.
A reatância contida nas placas dos transformadores são calculadas usando a potência nominal de operação como a potência de base para o sistema por unidade. Esta realidade aumenta a complexidade dos cálculos pois gera a necessidade de se inserir as relações de transformação nos cálculos das simulações. Para contornar esta complexidade, é possível recalcular a reatância dos transformadores utilizando um astuto artificio matemático que consiste na alteração da base atual de cálculo pela base de potência adotada pelo sistema. Este procedimento é conhecido como “mudança de base” e permite que os transformadores do sistema sejam representados por uma impedância simples nos cálculos das simulações de redes elétricas de potência.
Assim, os parâmetros elétricos dos transformadores do sistema representados em sistemas por unidade são sintetizados a seguir:
| Transformador | Zona de operação do primário |
Zona de operação do secundário |
Potência aparente nominal [MVA] |
Reatância elétrica (p.u) [%] |
Potência de base [MVA] |
Reatância elétrica em nova base (p.u) [%] |
|---|---|---|---|---|---|---|
| T1 | 0 | 1 | 50 | 5,5 | 100 | 11 |
| T2 | 0 | 1 | 25 | 6,5 | 100 | 26 |
| T3 | 1 | 2 | 25 | 6,5 | 100 | 26 |
| T4 | 1 | 2 | 25 | 6,5 | 100 | 26 |
| T5 | 1 | 2 | 15 | 8,5 | 100 | 57 |
| T6 | 1 | 2 | 5 | 12 | 100 | 240 |
Os parâmetros elétricos principais para a modelagem computacional dos transformadores no ANAREDE são a potencia aparente nominal [kVA] e a reatância elétrica em nova base (p.u) [%].
O ANAREDE permite a representação dos transformadores inseridos entre as barras no diagrama do sistema, tal como:
Modelagem das Linhas de Transmissão
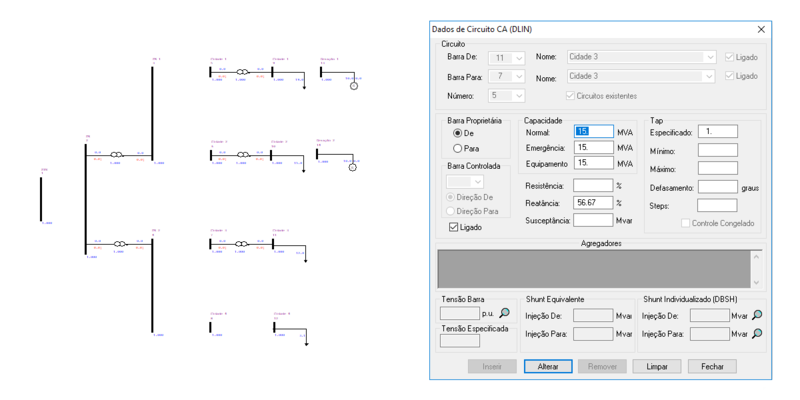
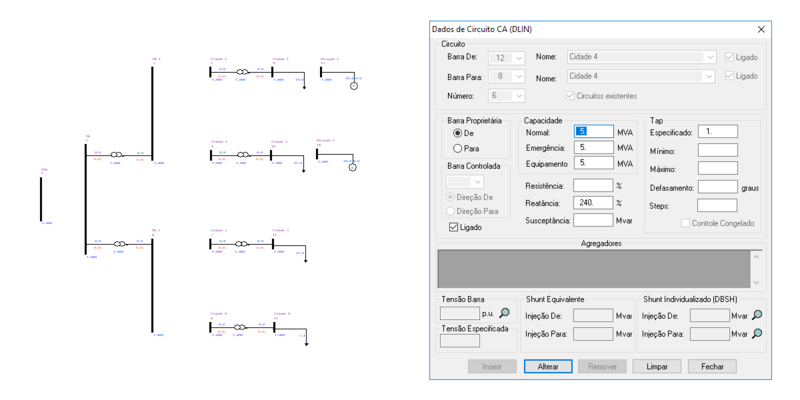
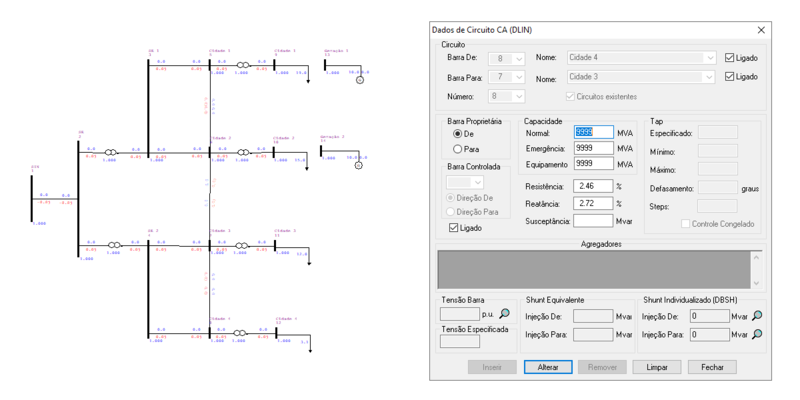
O sistema possui 8 linhas de transmissão, sendo LT1 uma linha de tamanho médio (80 km $\leq$ l $<$ 240 km) e as demais linhas (LT2, LT3, LT4, LT5, LT6, LT7 e LT8) de tamanho curto($<$ 80 km). Estas linhas podem ser representadas por seus circuitos equivalentes, respectivamente:

Os parâmetros das linhas de transmissão são requisitados conforme a sua representação:
- Linha média: $L$ (indutância) e $C$ (Capacitância), encontradas tendo como base, para $L$, o fluxo concatenado no condutor e a corrente que o produz e, para $C$, a tensão e a carga no condutor, em Coulombs por metro.
- Linha curta: $L$ (indutância), encontrada tendo como base o fluxo concatenado no condutor e a corrente que o produz.
Estes parâmetros são calculados conforme a geometria da linha de transmissão.
Para as linhas de transmissão de geometria equilateral, temos que:
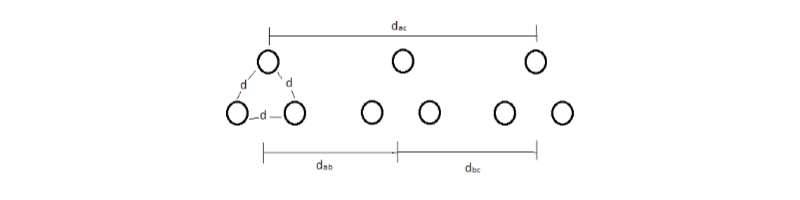
$ \displaystyle L=\frac{\mu_0}{2 \times \pi} \times \ln{ \displaystyle \frac{ \displaystyle \sqrt[ \displaystyle 3]{d_{ab}^2 \times d_{ac} }}{ \displaystyle \sqrt[ \displaystyle 3]{r \times e^{-1/4} \times d^2 }}} $
$ \displaystyle C=\frac{ \displaystyle 2 \times \pi \times \epsilon_0 }{ \displaystyle \ln { \left ( \displaystyle \frac{ \displaystyle \sqrt[ \displaystyle 3]{d_{ab}^2 \times d_{ac} }}{ \displaystyle \sqrt[ \displaystyle 3]{r \times e^{-1/4} \times d^2 }} \right ) } } \quad\,\,\,\, $
onde:
- $\mu_0$ constante de permeabilidade do vácuo;
- $\epsilon_0$ constante de permissividade do vácuo;
- $\pi$ constante pi;
- $r$ raio do condutor;
- $d$ distância entre os condutores;
- $d_{ab}$ distância entre os trios de condutores $a$ e $b$;
- $d_{ac}$ distância entre os trios de condutores $a$ e $c$;
- $d_{ab}$ distância entre os trios de condutores $a$ e $b$.
Para as linhas de transmissão de geometria linear, temos que:
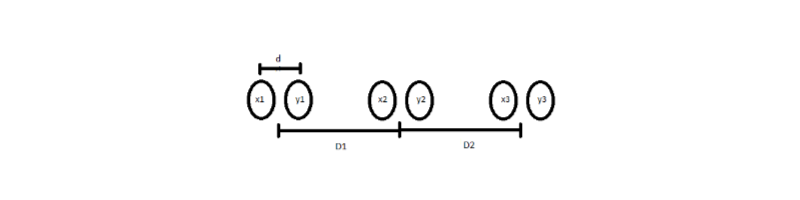
$ \displaystyle L=\frac{\mu_0}{2 \times \pi} \times \ln{ \displaystyle \frac{ \sqrt[ \displaystyle 3]{ DMG_{ab} \times DMG_{ac} \times DMG_{bc} } }{ \displaystyle \sqrt[ \displaystyle 3]{r \times e^{-1/4} \times d^2 }}} $
$ \small DMG_{ab}=\sqrt[ \displaystyle 4]{ D_1^2 \times ( D_1 + d ) \times d } \qquad\qquad\qquad\qquad\qquad\qquad\,\,\, $
$ \small DMG_{ac}=\sqrt[ \displaystyle 4]{ {(D_1+D_2)}^2 \times (D_1+D_2+d) \times (D_1+D_2-d) } \,\,\, $
$ \small DMG_{bc}=\sqrt[ \displaystyle 4]{ D_2^2 \times ( D_2 + d ) \times ( D_2-d ) } \qquad\qquad\qquad\qquad\,\,\,\,\,\, $
onde:
- $\mu_0$ constante de permeabilidade do vácuo;
- $\epsilon_0$ constante de permissividade do vácuo;
- $\pi$ constante pi;
- $r$ raio do condutor;
- $d$ distância entre os condutores;
- $D_1$ distância entre os pares de condutores $a$ e $b$;
- $D_2$ distância entre os pares de condutores $b$ e $c$.
Uma vez definidas as geometrias adotas e os modelos de condutores a serem utilizados é possível sintetizar as características mecânicas e elétricas das linhas de transmissão do sistema, dadas por:
| Linha | Modelo do Cabo |
Geometria | Comprimento [m] | Tipo | Raio do condutor [mm] |
|---|---|---|---|---|---|
| LT1 | 336,4 CAA – 26×7 f | Equilateral | 130 | Média | 9,16 |
| LT2 | 336,4 CA – 19 f | Linear | 10 | Curta | 8,45 |
| LT3 | 336,4 CA – 19 f | Linear | 12 | Curta | 8,45 |
| LT4 | 336,4 CA – 19 f | Linear | 7,5 | Curta | 8,45 |
| LT5 | 336,4 CA – 19 f | Linear | 8 | Curta | 8,45 |
| LT6 | 266,8 CA – 7 f |
Linear |
6,5 | Curta | 7,44 |
| LT7 | 266,8 CA – 7 f | Linear | 8 | Curta | 7,44 |
| LT8 | 266,8 CA – 7 f | Linear | 5,5 | Curta | 7,44 |
| Linha | Zona de operação |
Frequência de operação [ Hz ] |
Capacitância elétrica por metro [ F / m ] |
Indutância elétrica por metro [ H / m ] |
Resistência elétrica por metro [ $\Omega$ / m ] |
|---|---|---|---|---|---|
| LT1 | 0 | 60 | 1,35E-10 | 8,23E-07 | 1,70E-04 |
| LT2 | 1 | 60 | 0 | 5,51E-07 | 1,69E-04 |
| LT3 | 1 | 60 | 0 | 5,51E-07 | 1,69E-04 |
| LT4 | 1 | 60 | 0 | 5,51E-07 | 1,69E-04 |
| LT5 | 1 | 60 | 0 | 5,51E-07 | 1,69E-04 |
| LT6 | 1 | 60 | 0 | 6,24E-07 | 2,13E-04 |
| LT7 | 1 | 60 | 0 | 6,24E-07 | 2,13E-04 |
| LT8 | 1 | 60 | 0 | 6,24E-07 | 2,13E-04 |
Sintetizadas as características mecânicas e elétricas das linhas de transmissão do sistema é possível calcular seus parâmetros elétricos de operação, dados por:
| Linha | Capacitância elétrica [ F ] |
Reatância capacitiva [ $\Omega$ ] |
Indutância elétrica [ H ] |
Reatância indutiva [ $\Omega$ ] |
Resistência elétrica [ $\Omega$ ] |
|---|---|---|---|---|---|
| LT1 | 1,76E-06 | 4,66E-09 | 1,07E-01 | 7,63E-02 | 2,21E+01 |
| LT2 | 0 | 0 | 5,50E-03 | 4,43E-02 | 1,69E+00 |
| LT3 | 0 | 0 | 6,60E-03 | 5,31E-02 | 2,03E+00 |
| LT4 | 0 | 0 | 4,1E-03 | 3,32E-02 | 1,27E+00 |
| LT5 | 0 | 0 | 4,40E-03 | 3,54E-02 | 1,35E+00 |
| LT6 | 0 | 0 | 4,10E-03 | 3,32E-02 | 1,39E+00 |
| LT7 | 0 | 0 | 5,00E-03 | 4,08E-02 | 1,71E+00 |
| LT8 | 0 | 0 | 3,40E-03 | 2,81E-02 | 1,17E+00 |
Calculados os parâmetros elétricos de operação das linhas de transmissão do sistema é possível calcular os parâmetros elétricos das linhas de transmissão do sistema representados em sistemas por unidade, dados por:
| Linha | Admitância derivativa ou shunt (p.u) |
Reatância indutiva (p.u) |
Resistência elétrica (p.u) |
|---|---|---|---|
| LT1 | j0,3504 | 0,0763 | 0,0418 |
| LT2 | 0 | 0,0436 | 0,0355 |
| LT3 | 0 | 0,0524 | 0,0426 |
| LT4 | 0 | 0,0327 | 0,0266 |
| LT5 | 0 | 0,0349 | 0,0284 |
| LT6 | 0 | 0,0321 | 0,0291 |
| LT7 | 0 | 0,0395 | 0,0358 |
| LT8 | 0 | 0,0272 | 0,0281 |
Estes são os parâmetros elétricos principais para a modelagem computacional das linhas de transmissão. Os percentis destes parâmetros são apresentados abaixo:
| Linha | Admitância derivativa ou shunt (p.u) [%] |
Reatância indutiva (p.u) [%] |
Resistência elétrica (p.u) [%] |
|---|---|---|---|
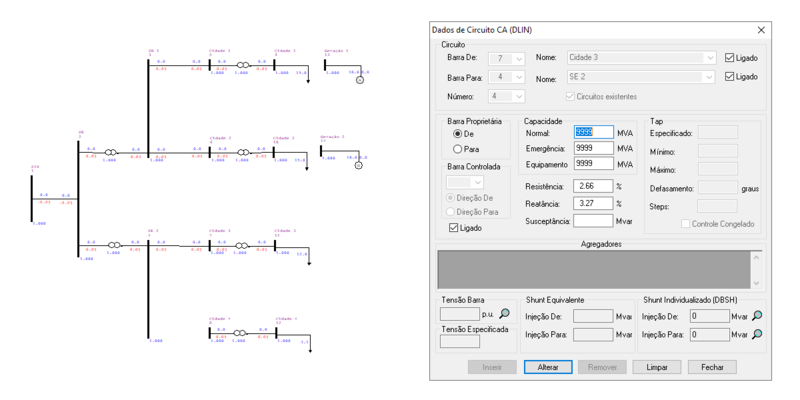
| LT1 | 35,04 | 7,63 | 4,18 |
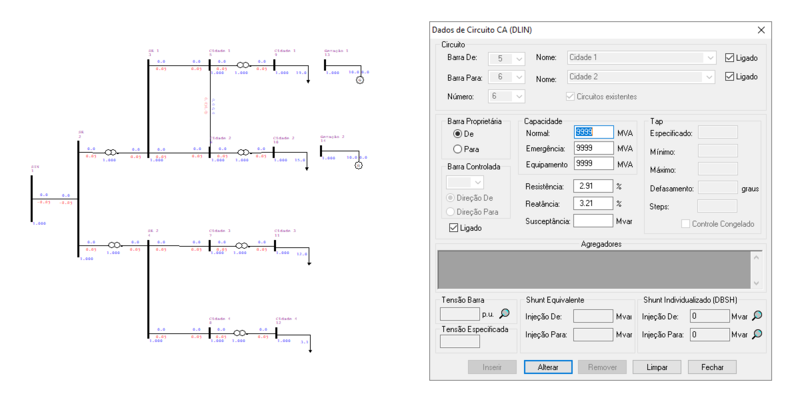
| LT2 | 0 | 4,36 | 3,55 |
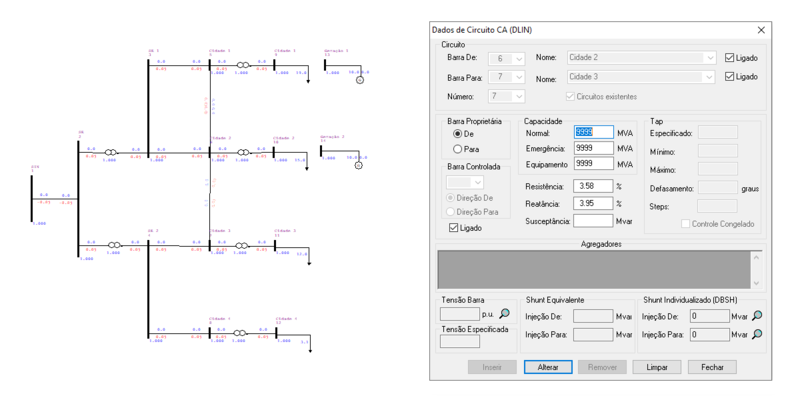
| LT3 | 0 | 5,24 | 4,26 |
| LT4 | 0 | 3,27 | 2,66 |
| LT5 | 0 | 3,49 | 2,84 |
| LT6 | 0 | 3,21 | 2,91 |
| LT7 | 0 | 3,95 | 3,58 |
| LT8 | 0 | 2,72 | 2,81 |
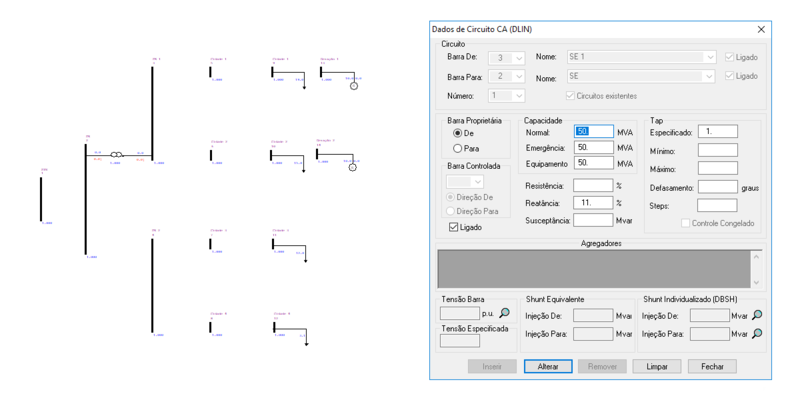
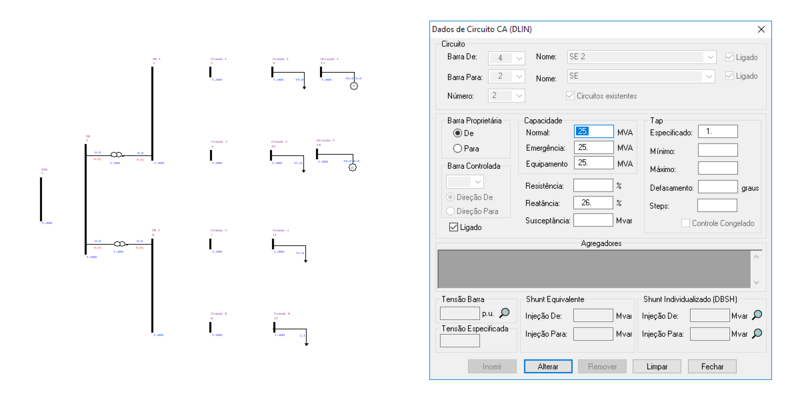
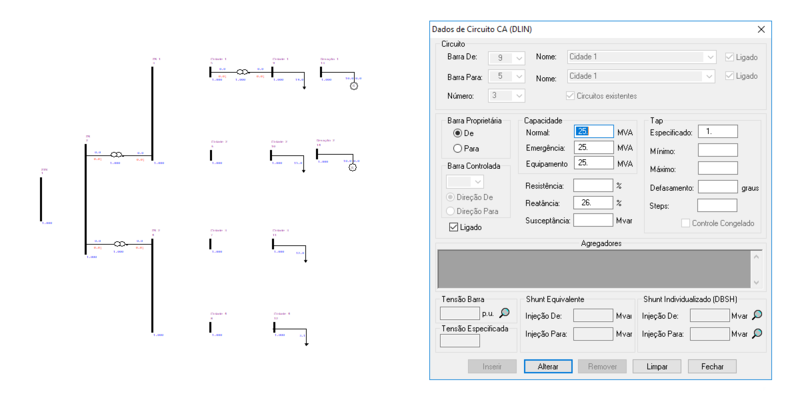
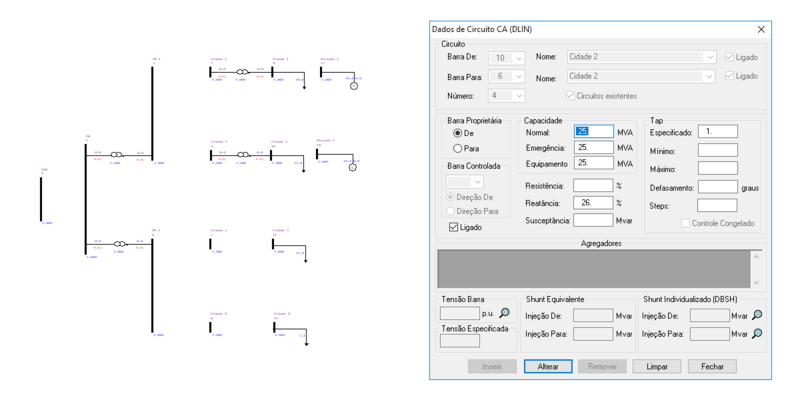
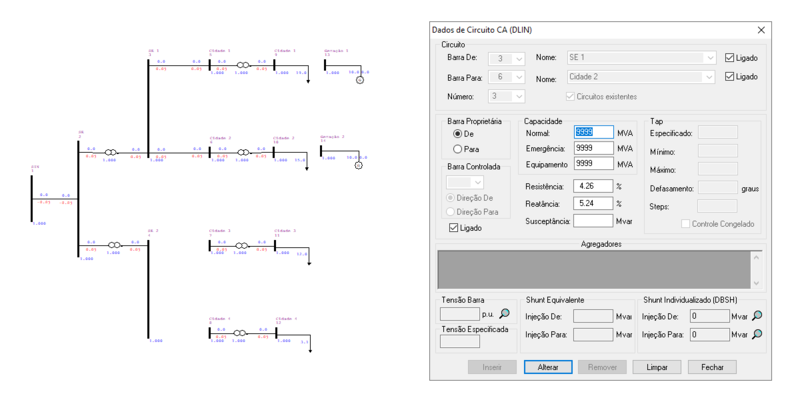
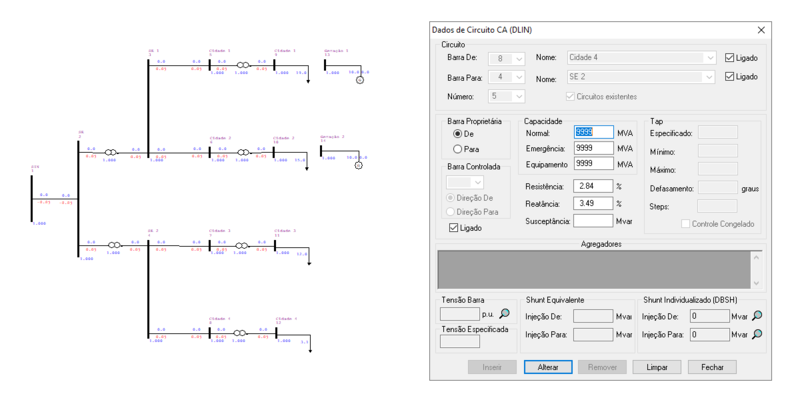
O ANAREDE permite a representação das linhas de transmissão entre as barras no diagrama do sistema, tal como:
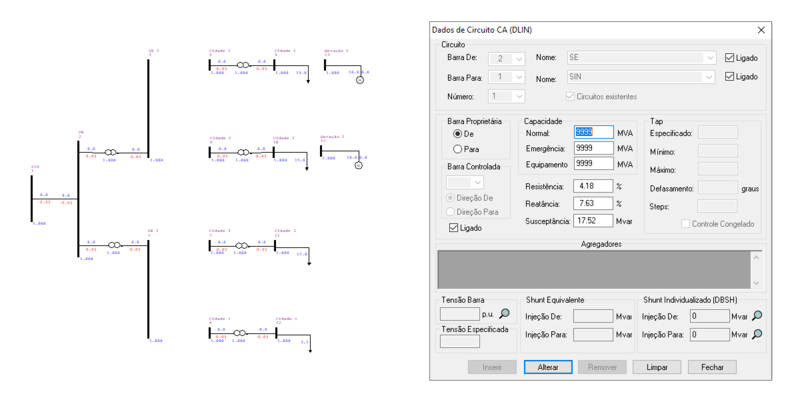
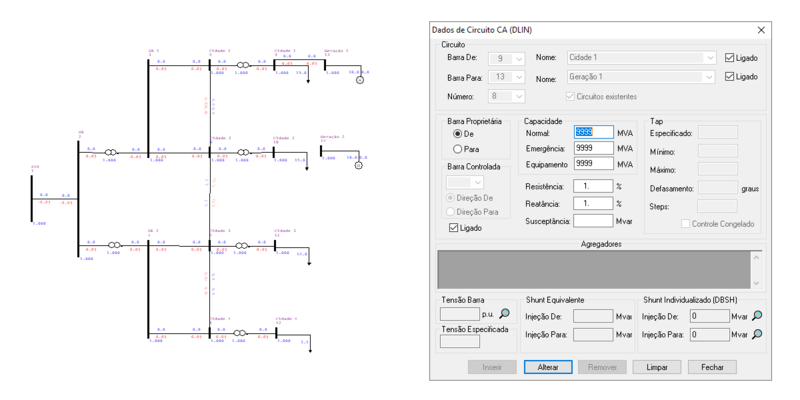
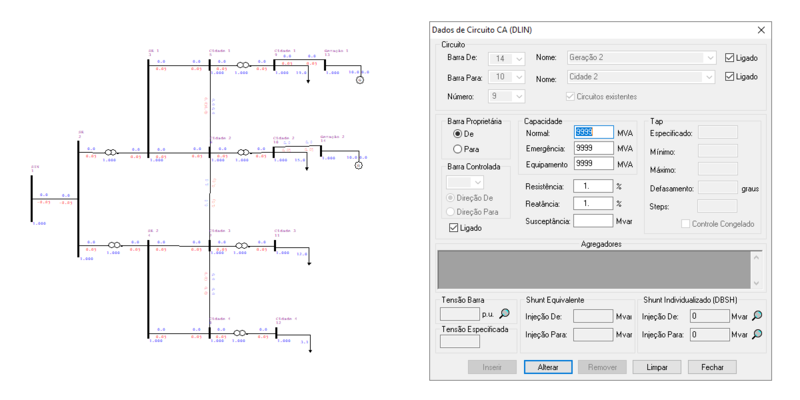
Adicionalmente, devem ser inseridas duas linhas de transmissão para a representação das conexões dos geradores ao circuito, tal como:
Mais do ANAREDE
- O ANAREDE;
- Dados de Base de Redes Elétricas;
- Diagrama de Redes Elétricas de Potência;
- Modelagem de um SEP no ANAREDE.
Referências
- Programa ANAREDE – Curso básico. <http://www.cepel.br/> Centro de Pesquisas de Energia Elétrica (CEPEL).
- Rocha, Ednardo P. da, Adriano F. Moura, Ednardo P. Rocha. Análise de Fluxo de Carga em Sistemas de Potência, Artliber, ISBN-10 8588098830, 2018.
- Manual do Usuário do ANAREDE v10.01.03, Centro de Pesquisas de Energia Elétrica (CEPEL), 2016.