O objetivo do comando do inversor por modulação de largura de pulso (PWM) é alimentar a máquina com tensões trifásicas variáveis a partir de um inversor trifásico de tensão.
A interpretação emprestada das telecomunicações explica este processo em duas fases:
1 – Modulação do sinal de tensão fundamental de referência segundo a alta frequência da portadora obtida pelo chaveamento do inversor de tensão.
2 – Demodulação ou recuperação do sinal fundamental de tensão através da corrente da máquina resultado da filtragem passa baixa da tensão modulada.
Quando se utiliza a implementação digital do PWM o inversor gera tensões instantâneas cujo valor médio em um intervalo de tempo é igual a tensão de referência.
O acionamento da máquina usando um inversor de tensão introduz componentes de alta frequência de corrente e conjugado e perdas no conversor.
Estas distorções e as perdas dependem do método de modulação empregado.
PWM seno $ X $ triângulo
O método PWM mais utilizado é denominado de seno $ X $ triângulo, é obtido a partir da comparação das tensões trifásicas de referencia $ v_{s1}^{s*} $, $ v_{s2}^{s*} $ e $ v_{s3}^{s*} $ com uma portadora triangular.
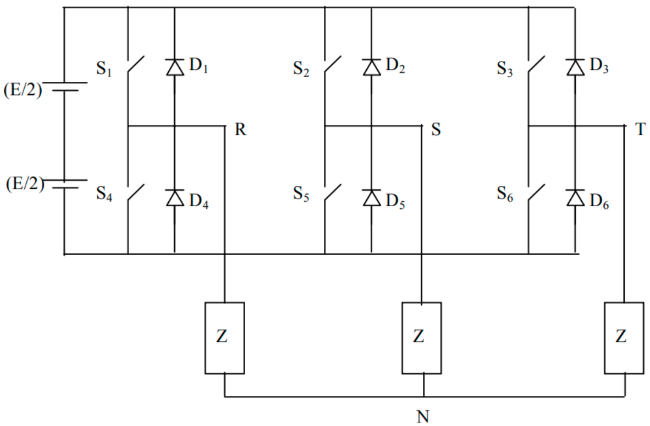

PWM seno X Triângulo. (a) Circuito equivalente (b) Sinais
A frequência do conversor é igual a da onda triangular, normalmente constante.


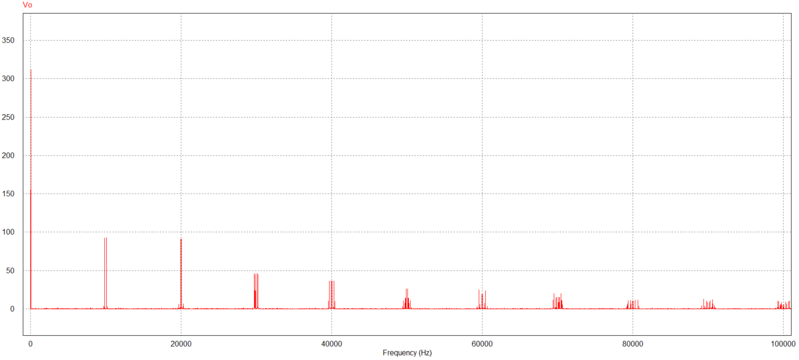
PWM seno X Triângulo. (a) Entrada portadora (b) $ V_{ao} $ no tempo. (c) $ V_{ao} $ na frequência.
Aplicar uma tensão com tal espectro de frequência é preocupante? sim.
Um dos problemas deste método é o baixo índice de modulação.
Definindo-se o índice de modulação como a razão entre a máxima tensão fundamental obtida com o método de modulação na região linear e a tensão fundamental do sinal seis steps.
$ \displaystyle \text{índice}_{max} = \frac{v_{ao,max}}{v_{an,max}} = \frac{350}{466,67} = 0,75 $
O índice pode ser aumentado adicionando uma componente homopolar em cada fase.
Comumente se adiciona um sinal com o triplo da frequência da fundamental.
Com isso obtém-se o índice de modulação máximo de $ 0,907 $.
O espectro de frequência do sinal de tensão se concentra em torno da portadora.
Métodos com frequência da portadora variável, mas com média constante, podem ser usados.
Tais métodos reduzem a distorção harmônica da tensão de saída do conversor, reduz o ruído audível e as vibrações da máquina.
Princípios do comando PWM
As técnicas de PWM digitais podem ser divididas em escalares e vetoriais.
Na abordagem escalar se opera com as tensões trifásicas por fase.
Na vetorial emprega-se o vetor tensão associado as tensões trifásicas.
Considere a figura contendo uma fonte CC, um VSI e uma máquina assíncrona.
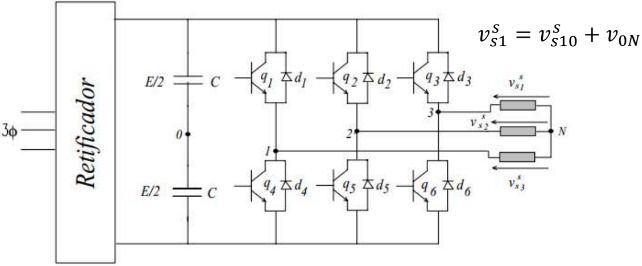
O ponto intermediário $ “0” $ é utilizado como referencia para as tensões.
O VSI possui $ 6 $ chaves e seus respectivos diodos de bloqueio.
As chaves $ q_1 $, $ q_2 $ e $ q_3 $ são complementares a $ q_4 $, $ q_5 $ e $ q_6 $.
Vamos considerar o estado da chave $ q_k = 1 $ como fechada e $ q_k = 0 $ como aberta. Logo,
$ \displaystyle \begin{cases}
q_4 = 1 – q_1 \\
q_5 = 1 – q_2 \\
q_6 = 1 – q_3
\end{cases} $
Dessa forma existem $ 2^3 = 8 $ combinações possíveis:
| Dec. | $ q_1 $ | $ q_2 $ | $ q_3 $ |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 |
| 4 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 |
| 6 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 |
Pela LKM as tensões de fase sobre a carga (máquina assíncrona) são
$ \displaystyle \begin{cases}
v_{s1}^s = v_{s10}^s + v_{0N} \\
v_{s2}^s = v_{s20}^s + v_{0N} \\
v_{s3}^s = v_{s30}^s + v_{0N}
\end{cases} $
Onde $ v_{0N} $ é a tensão entre o ponto intermediário e o neutro da carga.
$ \displaystyle \begin{cases}
v_{s10}^s = q_1 \frac{E}{2} – q_4 \frac{E}{2} = ( 2q_1 – 1 ) \frac{E}{2} \\
v_{s20}^s = q_2 \frac{E}{2} – q_5 \frac{E}{2} = ( 2q_2 – 1 ) \frac{E}{2} \\
v_{s30}^s = q_3 \frac{E}{2} – q_6 \frac{E}{2} = ( 2q_3 – 1 ) \frac{E}{2}
\end{cases} $
Logo, as tensões de fase na carga são
$ \displaystyle \begin{cases}
v_{s1}^s = ( 2q_1 – 1 ) \frac{E}{2} + v_{0N} \\
v_{s2}^s = ( 2q_2 – 1 ) \frac{E}{2} + v_{0N} \\
v_{s3}^s = ( 2q_3 – 1 ) \frac{E}{2} + v_{0N}
\end{cases} $
Modulação Vetorial (SVPWM)
As tensões estatóricas $ v_{sd}^s $ e $ v_{sq}^s $ no referencial estatórico $ ( \theta_s =0 \Rightarrow \alpha\beta ) $.
São obtidas em função das tensões $ v_{s1}^s $, $ v_{s2}^s $ e $ v_{s3}^s $ a partir da matriz de transformação.
$ \displaystyle \begin{bmatrix}
v_{s0}^s \\
v_{sd}^s \\
v_{sq}^s
\end{bmatrix}
=
\sqrt{\frac{2}{3}} \begin{bmatrix}
{\frac{1}{\sqrt{2}}} & {\frac{1}{\sqrt{2}}} & {\frac{1}{\sqrt{2}}} \\
1 & {-\frac{1}{2}} & {-\frac{1}{2}} \\
0 & {\frac{\sqrt{3}}{2}} & {-\frac{\sqrt{3}}{2}}
\end{bmatrix}
\begin{bmatrix}
v_{s1}^s \\
v_{s2}^s \\
v_{s3}^s
\end{bmatrix}$
$ \displaystyle \begin{bmatrix}
v_{sd}^s \\
v_{sq}^s
\end{bmatrix}
=
\begin{bmatrix}
\sqrt{\frac{2}{3}}\left( q_1-\frac{q_2}{2}-\frac{q_3}{2} \right)E \\
\frac{1}{\sqrt2}\left(q_2-q_3\right)E
\end{bmatrix}$
Tais tensões independem de $ v_{0N} $.
Dada a matriz, obtém-se $ 6 $ vetores não nulos e $ 2 $ vetores nulos, um para cada combinação de chaveamento:
$ \displaystyle V_{sk}^s = V_{sd}^s + jV_{sq}^s = V_{sk}\angle\delta_{sk} $
onde,
$ \qquad V_{sk}^s \rightarrow $ Modulo da tensão.
$ \qquad \delta_{sk} \rightarrow $ Ângulo em relação ao eixo $ s_1 $.
Portanto,
$ \displaystyle V_{sk}^s = \sqrt{\frac{2}{3}}\left( q_1-\frac{q_2}{2}-\frac{q_3}{2} \right)E + j\frac{1}{\sqrt2}\left(q_2-q_3\right)E $
e seus respectivos vetores são
| $ q_1 $ | $ q_2 $ | $ q_3 $ | Vetores |
| 1 | 0 | 0 | $ V_{s1}^s = \sqrt{\frac{2}{3}}E\angle0 \qquad $ |
| 1 | 1 | 0 | $ V_{s2}^s = \sqrt{\frac{2}{3}}E\angle\pi/3 \quad $ |
| 0 | 1 | 0 | $ V_{s3}^s = \sqrt{\frac{2}{3}}E\angle2\pi/3 $ |
| 0 | 1 | 1 | $ V_{s4}^s = \sqrt{\frac{2}{3}}E\angle\pi \qquad $ |
| 0 | 0 | 1 | $ V_{s5}^s = \sqrt{\frac{2}{3}}E\angle4\pi/3 $ |
| 1 | 0 | 1 | $ V_{s6}^s = \sqrt{\frac{2}{3}}E\angle5\pi/3 $ |
| 0 | 0 | 0 | $ V_{s7}^s = 0 \quad\qquad\qquad $ |
| 1 | 1 | 1 | $ V_{s8}^s = 0 \quad\qquad\qquad $ |
Os seis vetores não-nulos definem seis setores de $ 60^\circ $ identificados por $ I $, $ II $, $ III $, $ IV $, $ V $ e $ VI $.

Um vetor de referência no plano $ dq $ pode ser obtido em termos médios num período de amostragem $ \tau $ utilizando-se um mínimo de dois, dentre os seis vetores não nulos.
Para minimizar a frequência de operação do conversor utiliza-se os dois vetores adjacentes ao vetor de referência $ v_s^{s*} $.
Geometricamente, dado um vetor de referencia $ v_s^{s*} $, constante em período $ \tau $, e os dois vetores adjacentes $ V_{sk}^s $ e $ V_{sl}^s $, onde:
$ \displaystyle \begin{cases}
k = 1, \dotso, 6 \\
l = k+1, \quad \,\, se \quad k \leqslant 5 \\
l = 1, \quad \qquad se \quad k = 6
\end{cases} $
temos,
$ \displaystyle \frac{1}{\tau}\int_{0}^{\tau_k}v_{s}^{s*}dt = \frac{1}{\tau}\int_{0}^{\tau_k}V_{sk}^sdt+\frac{1}{\tau}\int_{0}^{\tau_l}V_{sl}^sdt $
Logo,
$ \displaystyle v_{s}^{s*} = \frac{\tau_k}{\tau}V_{sk}^s+\frac{\tau_l}{\tau}V_{sl}^s $
Onde $ \tau_k $ e $ \tau_l $ são os intervalos no tempo de aplicação dos vetores $ V_{sk}^s $ e $ V_{sl}^s $, respectivamente.
Explicitando-se a equação vetorial em termo dos componentes $ dq $, tem-se
$ \displaystyle v_{sd}^{s*} = \frac{\tau_k}{\tau}V_{sdk}^s+\frac{\tau_l}{\tau}V_{sdl}^s $
$ \displaystyle v_{sq}^{s*} = \frac{\tau_k}{\tau}V_{sqk}^s+\frac{\tau_l}{\tau}V_{sql}^s $
Dessa forma,
$ \displaystyle {\tau_k}={\frac{V_{sql}^s v_{sd}^{s}-V_{sdl}^s v_{sq}^{s}}{V_{sdk}^s V_{sql}^{s}-V_{sdl}^s V_{sqk}^{s*}}\tau} $
$ \displaystyle {\tau_l ={\frac{V_{sdl}^s v_{sq}^{s}-V_{sqk}^s v_{sd}^{s}}{V_{sdk}^s V_{sql}^{s}-V_{sdl}^s V_{sqk}^{s*}}\tau} $
Para que a frequência do conversor seja constante é necessário que a soma dos tempos dos vetores aplicados seja igual a $ \tau $.
Assim, aplica-se os vetores nulos, que não geram tensão media, de forma que a condição de frequência constante seja observada.
Note que os vetores não nulos são obtidos quando a máquina opera em curto-circuito (roda-livre).
$ \displaystyle \tau_0+\tau_k+\tau_l=\tau $
O $ \tau_0 $ pode ser dividido no começo em $ \tau_{0i} $ e no fim em $ \tau_{0f} $.
Com esse procedimento é possível minimizar a distorção harmônica da corrente da máquina distribuindo os vetores nulos no início $ (\tau_{0i}) $ ou no fim $ (\tau_{0f}) $.
$ \displaystyle \tau_0 = \tau_{0i} + \tau_{0f} = \tau-\tau_{k}-\tau_{l} $
Introduzindo o fator de distribuição da roda livre inicial
$ \displaystyle \mu=\frac{\tau_{0i}}{\tau_{0i}+\tau_{0f}} $
$ \displaystyle \tau_{0i}=\mu\tau_0 $
$ \displaystyle \tau_{0f}=(1-\mu)\tau_0 $
Adotemos como exemplo o acionamento de um inversor de tensão com $ V_{d} = 700V $ para que o mesmo possua em sua saída uma tensão de $ 220V $ RMS e frequência de amostragem a $ 10kHz $ para alimentar uma carga de $ 10 \Omega $ e $ 10mH $ utilizando PWM seno $ X $ triângulo e utilizando modulação vetorial.
Corrente esperada na fundamental
$ \displaystyle I = \frac{220}{10+j(2\pi)(60)(10\times10^{-3})} = 20,58\angle-20,65^{\circ} \, A $

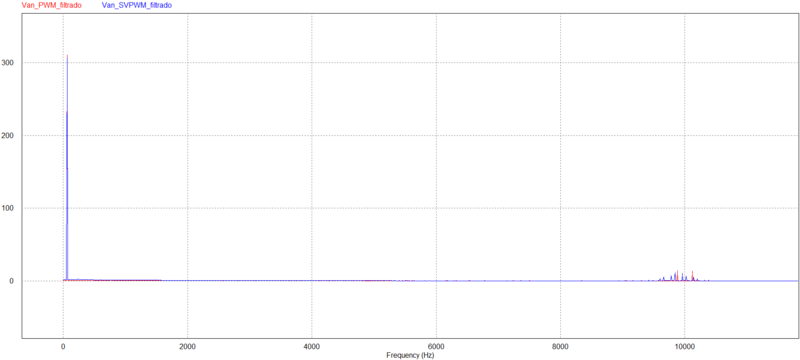

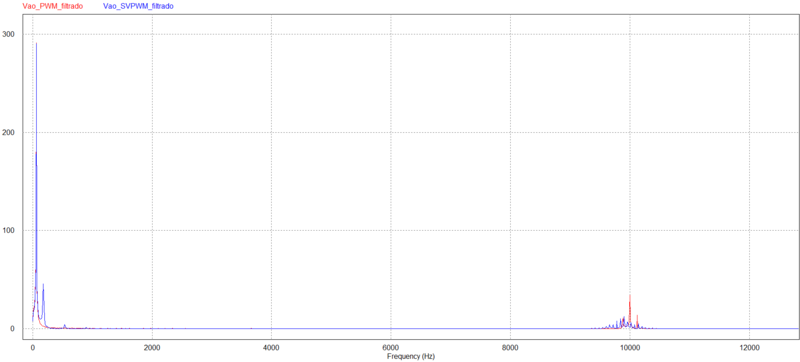
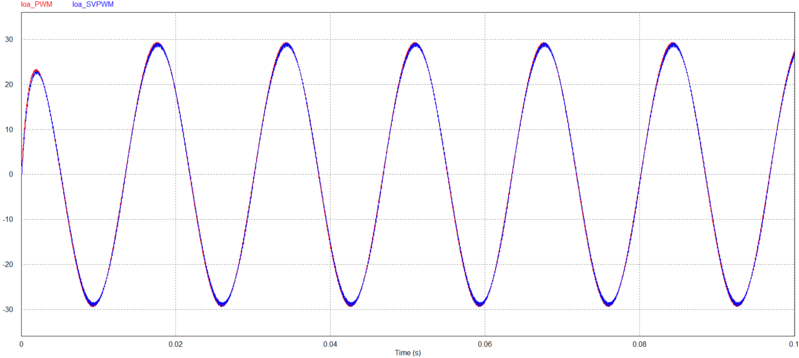

PWM seno X Triângulo x SVPWM $ 220V $ RMS. (a) $ V_{an} $ no tempo. (b) $ V_{an} $ na frequência. (c) $ V_{ao} $ no tempo. (d) $ V_{ao} $ na frequência (e) $ I_{ao} $ no tempo. (d) $ I_{ao} $ na frequência.
Agora adotemos como exemplo o acionamento de um inversor de tensão similar ao anterior, mas que desta vez possua em sua saída uma tensão de $ 282,84V $ RMS utilizando PWM seno $ X $ triângulo e utilizando modulação vetorial.
Corrente esperada na fundamental
$ \displaystyle I = \frac{282,84}{10+j(2\pi)(60)(10\times10^{-3})} = 26,46\angle-20,65^{\circ} \, A $
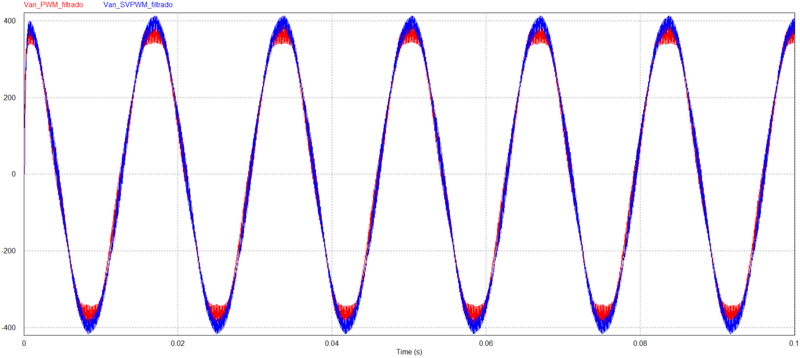

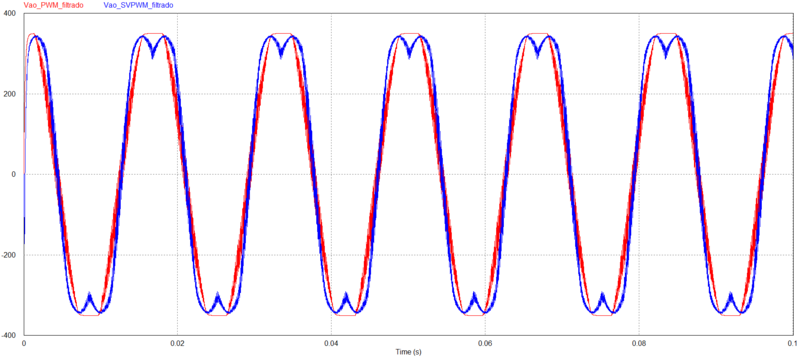



PWM seno X Triângulo x SVPWM $ 282,84V $ RMS. (a) $ V_{an} $ no tempo. (b) $ V_{an} $ na frequência. (c) $ V_{ao} $ no tempo. (d) $ V_{ao} $ na frequência (e) $ I_{ao} $ no tempo. (f) $ I_{ao} $ na frequência.
Modulação Vetorial com Pulso Espelhado
Em geral é interessante inverter a sequência de aplicação dos dois vetores não nulos no início de cada período $ \tau $ (espelhamento), reduzindo o número de chaveamento, mantendo o mesmo número de comutações.
Se os vetores $ V_{s1}^s $, $ V_{s2}^s $ e $ V_{s0}^s $ são aplicados no próximo período $ \tau $: $ V_{s0}^s $, $ V_{s2}^s $ e $ V_{s1}^s $.
$ \displaystyle \left[ \quad V_{s0}^s \{ t_{oi} \}, \quad V_{s1}^s \{ t_1 \}, \quad V_{s2}^s \{ t_2 \}, \quad V_{s7}^s \{ t_{of} \} \quad \right] \quad-\quad \left[ V_{s7}^s \{ t_{of}^{\prime} \}, \quad V_{s2}^s \{ t_2^{\prime} \}, \quad V_{s1}^s \{ t_1^{\prime} \}, \quad V_{s0}^s \{ t_{oi}^{\prime} \} \right] $


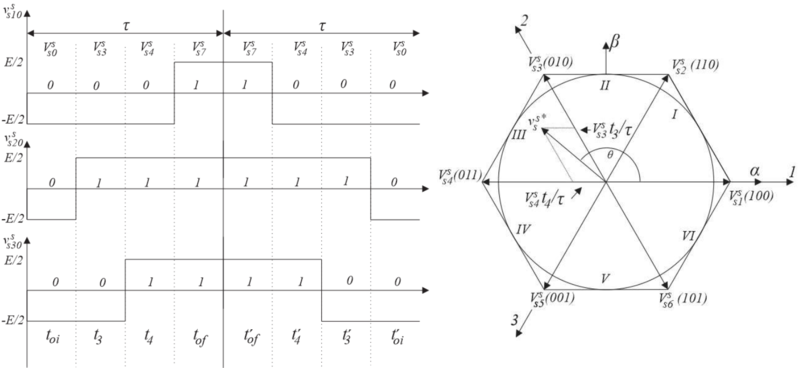

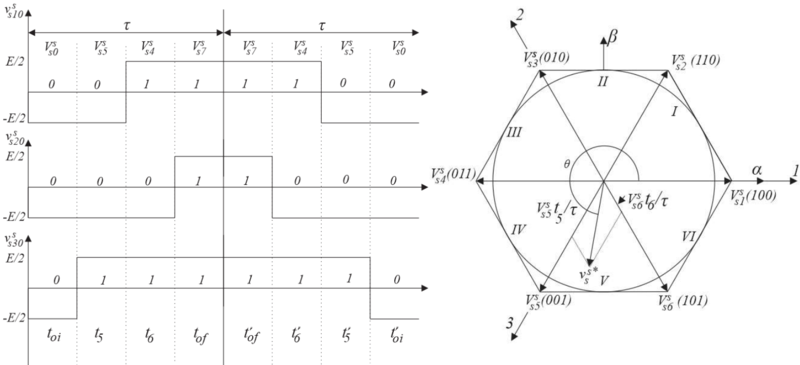
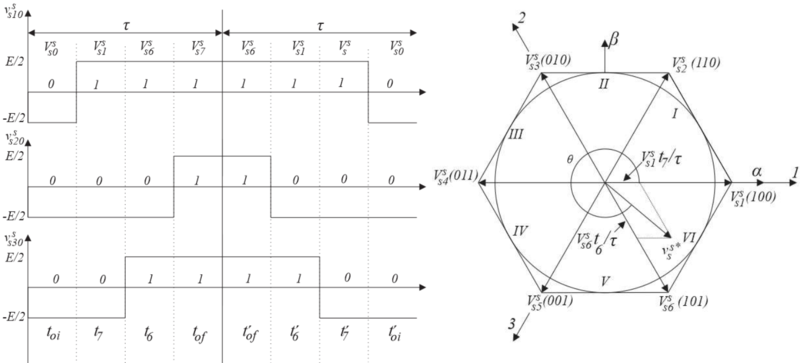
Modulação Vetorial com Pulso Espelhado. (a) Setor 1. (b) Setor 2. (c) Setor 3. (d) Setor 4. (e) Setor 5. (f) Setor 6.
Atentar a alteração das ocorrências dos períodos $ t_{k} $ e $ t_{l} $ nos setores pares.
Adotemos novamente como exemplo o acionamento de um inversor de tensão com $ V_{d} = 700V $ para que o mesmo possua em sua saída uma tensão de $ 220V $ RMS e frequência de amostragem a $ 10kHz $ para alimentar uma carga de $ 10 \Omega $ e $ 10mH $, desta vez utilizando modulação vetorial com pulso espelhado.
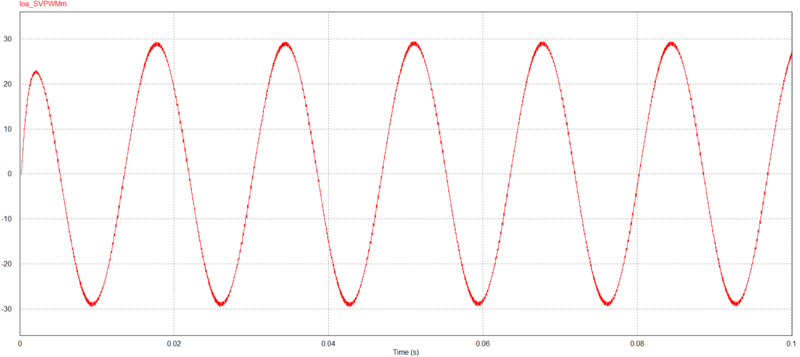


SVPWM espelhado $ 220V $ RMS e 10kHz. (a) $ I_{ao} $ no tempo. (b) $ I_{ao} $ na frequência. (c) Chaveamento do inversor.
Agora adotemos como exemplo o acionamento de um inversor de tensão similar ao anterior, em que, desta vez, se adote uma frequência de amostragem de $ 20kHz $.

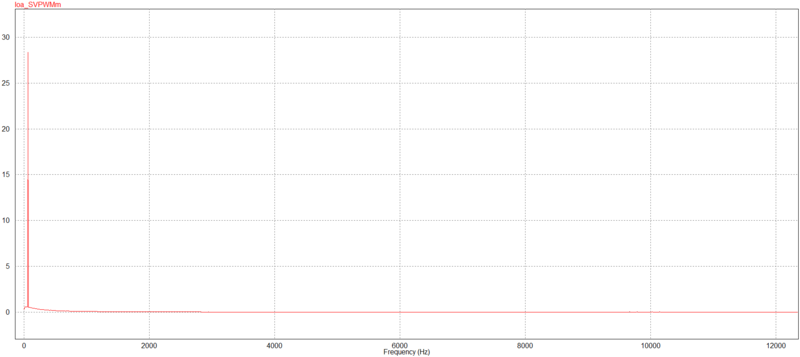

SVPWM espelhado $ 220V $ RMS e 20kHz. (a) $ I_{ao} $ no tempo. (b) $ I_{ao} $ na frequência. (c) Chaveamento do inversor.
Podemos observar que ao utilizar modulação vetorial espelhada reduzimos o número de chaveamento ao custo da redução da precisão na representação da corrente na saída do conversor. No entanto, podemos obter esta precisão dobrando a frequência de amostragem, o que reduz o período de mostragem pela metade na modulação vetorial.
Modulação Escalar
A partir das tensões de referência é possível obter os tempos de operação das chaves.
$ \displaystyle \begin{cases}
v_{s10}^{s*} = v_{s1}^{s*} + v_h \\
v_{s20}^{s*} = v_{s2}^{s*} + v_h \\
v_{s30}^{s*} = v_{s3}^{s*} + v_h
\end{cases} $
onde $ v_h $ é a componente homopolar. A tensão média por fase independe dela.
Considerando que as tensões $ v_{s1230}^{s*} $ são as tensões médias de referencia e que $ \bar{v}_{s1230}^{s} $ são os valores médios das tensões instantâneas aplicadas pelo VSI.
$ \displaystyle \begin{cases}
\frac{1}{\tau}\int_{0}^{\tau}v_{s10}^{s*}dt = v_{s10}^{s*} = \frac{1}{\tau}\int_{0}^{\tau}v_{s10}^sdt = \bar{v}_{s10}^s = [\frac{E}{2}\tau_1-\frac{E}{2}(\tau-\tau_1)]\frac{1}{\tau} \\
\frac{1}{\tau}\int_{0}^{\tau}v_{s20}^{s*}dt = v_{s20}^{s*} = \frac{1}{\tau}\int_{0}^{\tau}v_{s20}^sdt = \bar{v}_{s20}^s = [\frac{E}{2}\tau_2-\frac{E}{2}(\tau-\tau_2)]\frac{1}{\tau} \\
\frac{1}{\tau}\int_{0}^{\tau}v_{s30}^{s*}dt = v_{s30}^{s*} = \frac{1}{\tau}\int_{0}^{\tau}v_{s30}^sdt = \bar{v}_{s30}^s = [\frac{E}{2}\tau_3-\frac{E}{2}(\tau-\tau_3)]\frac{1}{\tau}
\end{cases} $
A partir das tensões de referencia é possível obter os tempos de operação das chaves.
$ \displaystyle \begin{cases}
\tau_{1} = (\frac{v_{s10}^{s*}}{E}+\frac{1}{2})\tau \\
\tau_{2} = (\frac{v_{s20}^{s*}}{E}+\frac{1}{2})\tau \\
\tau_{3} = (\frac{v_{s30}^{s*}}{E}+\frac{1}{2})\tau
\end{cases} $
As tensões de polos são iguais aos valores de $ v_{s123}^{s*} $.
$ \displaystyle \begin{cases}
\bar{v}_{s1}^s = \bar{v}_{s10}^s + \bar{v}_{0N} = v_{s1}^{s*} + v_h + \bar{v}_{0N} \\
\bar{v}_{s2}^s = \bar{v}_{s20}^s + \bar{v}_{0N} = v_{s2}^{s*} + v_h + \bar{v}_{0N} \\
\bar{v}_{s3}^s = \bar{v}_{s30}^s + \bar{v}_{0N} = v_{s3}^{s*} + v_h + \bar{v}_{0N}
\end{cases} $
$ \displaystyle \bar{v}_{s1}^{s} + \bar{v}_{s2}^{s} + \bar{v}_{s3}^{s} = v_{s1}^{s*} + v_{s2}^{s*} + v_{s3}^{s*} + 3(v_h + \bar{v}_{0N} ) $
Para uma máquina ligada em estrela e simétrica temos
$ \displaystyle \begin{cases}
\bar{v}_{s1}^{s} = v_{s1}^{s*} \\
\bar{v}_{s2}^{s} = v_{s2}^{s*} \\
\bar{v}_{s3}^{s} = v_{s3}^{s*} \\
v_h \,\, = -\bar{v}_ {0N} \end{cases} $
Utilizando o referencial estacionário obtemos
$ \displaystyle \begin{cases}
v_{s1}^{s*} = \sqrt{\frac{2}{3}}v_{sd}^{s*} \\
v_{s2}^{s*} = -\frac{1}{\sqrt{6}}(v_{sd}^{s*}-\sqrt{3}{v_{sq}^{s*}}) \\
v_{s3}^{s*} = -\frac{1}{\sqrt{6}}(v_{sd}^{s*}+\sqrt{3}{v_{sq}^{s*}}) \end{cases} $
e
$ \displaystyle \begin{cases}
\tau_{1} = (\sqrt{\frac{2}{3}}\frac{v_{sd}^{s*}}{E}+\frac{1}{2})\tau + \frac{v_h}{E}\tau \\
\tau_{2} = (-\frac{1}{\sqrt{6}}\frac{v_{sd}^{s*}-\sqrt{3}{v_{sq}^{s*}}}{E}+\frac{1}{2})\tau + \frac{v_h}{E}\tau \\
\tau_{3} = (-\frac{1}{\sqrt{6}}\frac{v_{sd}^{s*}+\sqrt{3}{v_{sq}^{s*}}}{E}+\frac{1}{2})\tau + \frac{v_h}{E}\tau
\end{cases} $
Expressando a componente homopolar em função do $ \mu $ temos
$ \displaystyle v_h = E(\frac{1}{2}-\mu)-(1-\mu)v_{sM}^{s*}-\mu v_{sm}^{s*} $
onde $ v_{sM}^{s*} $ e $ v_{sm}^{s*} $ são os valores máximos e mínimos das tensões de referência.
Pode-se fazer a inversão da aplicação dos tempos como na modulação vetorial.

Relação entre as modulações vetorial e escalar
Expressando a componente homopolar em função do $ \mu $

Para o primeiro setor $ k = 1 $ e $ l = 2 $.
$ \displaystyle \tau_1 = \frac{1}{\sqrt{2}}\frac{\tau}{E}(\sqrt{3}v_{sd}^{s*}-v_{sq}^{s*}) $
$ \displaystyle \tau_2 = \sqrt{2}\frac{\tau}{E}v_{sq}^{s*} \quad\qquad\qquad $
Para um ciclo completo da fundamental temos
$ \displaystyle \tau_k = \tau_M-\tau_i $ (setor impar)
$ \displaystyle \tau_k = \tau_i-\tau_m $ (setor par)
$ \displaystyle \tau_l = \tau_i-\tau_m $ (setor impar)
$ \displaystyle \tau_l = \tau_M-\tau_i $ (setor par)
onde,
$ \qquad \tau_M \rightarrow $ Tempo no valor máximo.
$ \qquad \tau_m \rightarrow $ Tempo no valor mínimo.
$ \qquad \tau_i \rightarrow $ Tempo no valor intermediário.
$ \tau_M $ e $ \tau_m $ se relacionam com $ v_{sM}^{s*} $ e $ v_{sm}^{s*} $.

Genericamente,
$ \displaystyle \tau_{oi} = \tau-\tau_M \qquad $ e $ \displaystyle \qquad \tau_{of} = \tau_m $
$ \displaystyle \tau_{0} = \tau_{oi}+\tau_{off} = \tau-\tau_M+\tau_m $
| Modulação |
| Vetorial | Escalar |
| Setor I – $ (V_1^s-V_2^s) $ | $ \tau_1 > \tau_2 > \tau_3 $ |
| Setor II – $ (V_2^s-V_3^s) $ | $ \tau_2 > \tau_1 > \tau_3 $ |
| Setor III – $ (V_3^s-V_4^s) $ | $ \tau_2 > \tau_3 > \tau_1 $ |
| Setor IV – $ (V_4^s-V_5^s) $ | $ \tau_3 > \tau_2 > \tau_1 $ |
| Setor V – $ (V_5^s-V_6^s) $ | $ \tau_3 > \tau_1 > \tau_2 $ |
| Setor VI – $ (V_6^s-V_1^s) $ | $ \tau_1 > \tau_3 > \tau_2 $ |
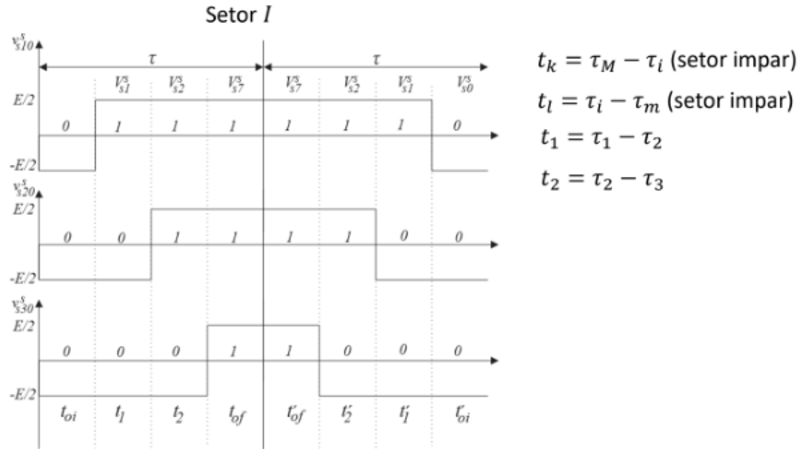

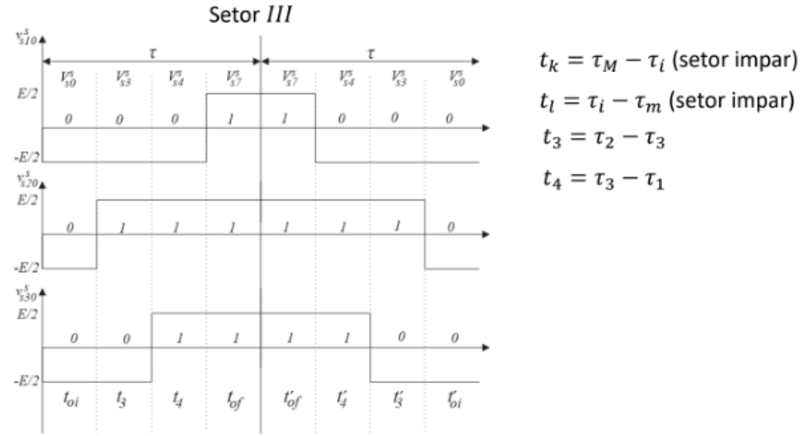

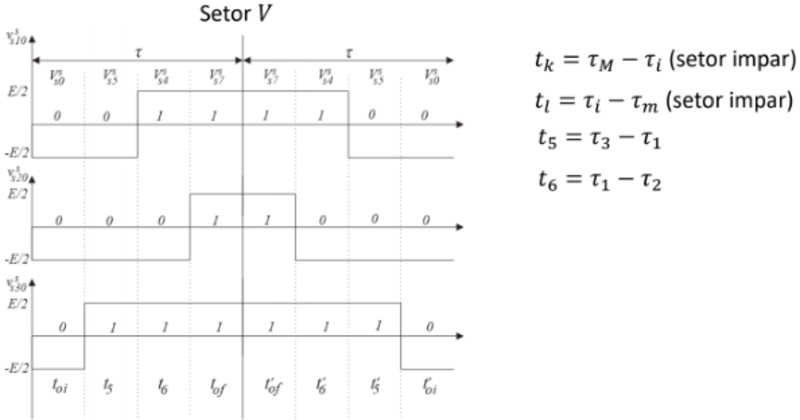
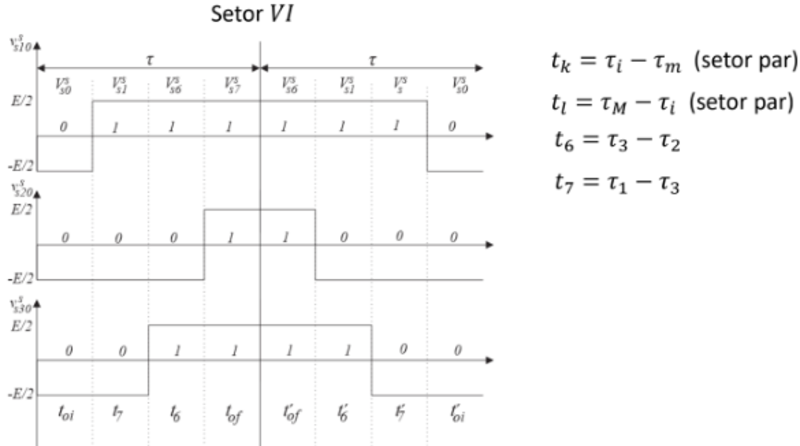
Modulação Vetorial com Pulso Espelhado x Modulação Escalar. (a) Setor 1. (b) Setor 2. (c) Setor 3. (d) Setor 4. (e) Setor 5. (f) Setor 6.
Referências
- Notas de aula do prof. dr. Caio Dorneles Cunha e prof. dr. Thiago de Oliveira Alves Rocha.
- Mohan, Undeland e Robbins, Power Electronics. Willey, 1989.
- W. Leonard, Control of Electrical Drives. Springer, 2001 2Ed.
- M. E. El-Hawary, Modeling and High Performance Control of Electric Machines. John Wiley & Sons, 2005.
- Chen-Mun Ong, Dynamic Simulation of Electric Machinery. Prentice-Hall, 1997.
- R. Krishnan, Eletric Motor Drives, Modeling, Analysis, and Control. Prentice-Hall, 2001.
- Ned Mohan, Máquinas Elétricas e Acionamentos. LTC, 2015.
- Ivo Barbi, Teoria Fundamental do Motor de Indução. Editora da UFSC/ELETROBRÁS, 1985.
