Um fasor se constitui em um vetor girante utilizado para representar uma grandeza escalar que varia em relação à variável independente (tempo, posição ou alguma outra variável de interesse) de acordo com uma função harmônica (seno, cosseno). Portanto um fasor é uma representação geométrica prática, interessante, operacional de descrever uma grandeza escalar. Portanto nem todo vetor é um fasor
Um vetor de fase ou fasor é uma representação de uma função senoidal cuja amplitude $ (A) $, frequência angular $ (\omega) $ e fase $ (\theta) $ são invariantes no tempo.
$ \displaystyle x(t) = A.sin(\omega t \pm \theta) $
O diagrama fasorial é utilizado na análise de circuitos de corrente alternada (CA) por permitir analisar a tensão e a corrente de forma facilitada, possibilitando, por exemplo, a análise da defasagem. A tensão elétrica em um circuito CA monofásico pode ser representada por
$ \displaystyle v(t) = V_m.sin(\omega t \pm \theta_v) $

(a) Diagrama fasorial. (b) Onda senoidal resultante.
Na representação fasorial, a soma de vários fasores de mesma frequência angular $ (\omega) $ produz outro fasor.

(a) Diagramas fasoriais. (b) Ondas resultantes.
Nestes casos, a frequência angular $ (\omega) $ pode ser omitida do equacionamento para o cálculo dos valores representativos de cada fasor, uma vez que estes podem ser observados do mesmo ponto referencial $ (t=0) $.
Logo, as características resistivas e reativas de um circuito CA monofásico e trifásico podem ser representadas por meio de diagramas fasoriais.
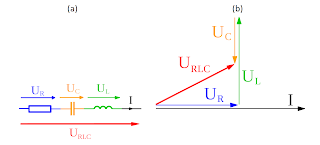
(a) Circuito RLC série. (b) Diagramas fasoriais.
Sistemas trifásicos são sistemas que possuem três tensões de fases de mesmo valor eficaz defasados de $ 120^\circ $ entre si. Devemos prestar atenção especial à representação trigonométrica, pois ela exige que o valor da tensão ou corrente que multiplica a senoide seja a tensão ou corrente de valor máximo. Assim, se estivermos trabalhando com tensão eficaz $ (V_{ef}) $ ou corrente eficaz $ (I_{ef}) $, devemos multiplicar o valor eficaz por $ 2 $ para calcularmos o valor máximo da tensão $ (V_m) $ ou corrente $ (I_m) $.
$ \displaystyle {\dot{V}_S}={{\sqrt{2}}{V_{ef}}{\left[ cos(\theta) \pm j.sin(\theta) \right]}}={V_m\angle (\theta)} \qquad\qquad\qquad\qquad\quad\,\, $
$ \displaystyle {\dot{V}_T}= {{\sqrt{2}}{V_{ef}}{\left[ cos(\theta-120^\circ) \pm j.sin(\theta-120^\circ) \right]}= V_m\angle (\theta-120^\circ)} $
$ \displaystyle {\dot{V}_R}= {{\sqrt{2}}{V_{ef}}\left[ cos(\theta+120^\circ) \pm j.sin(\theta+120^\circ) \right] = V_m\angle (\theta+120^\circ)} $

(a) Diagramas fasoriais. (b) Ondas resultantes.
Exemplo
No circuito abaixo, considerando que a fonte de tensão é $ V_S (t) = 7,28.\cos(2.t+47^\circ) \, [V] $ e a tensão no resistor é $ V_R(t) = 1,59.cos(2.t+125^\circ) \, [V] $.
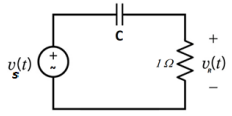
Podemos observar que,
$ \displaystyle \omega_s = \omega_R = 2 \,[rad/s] $
Logo, podemos omitir a velocidade angular $\omega$ da representação dos fasores. Desta forma,
$ \displaystyle V_S = 7,28.\cos(47^\circ) = 4,97 \, [V] \qquad\qquad\,\, $
$ \displaystyle V_R = 1,59.cos(125^\circ) = -9,12\times10^{-1} \, [V] $
Pela 1ª e 2ª Lei de Kirchhoff, calculamos, receptivamente
$ \displaystyle V_C = V_S-V_R=5,882 \, [V] $
$ \displaystyle I_S=I_C=I_R=I=\frac{V_R}{R}=1,25 \, [A] $
Portanto, a capacitância C do capacitor é, aproximadamente,
$ \displaystyle C=\frac{I}{\omega V_C}=0,106 \,[mF] $
Referências
- BURIAN JUNIOR, Yaro; LYRA, Ana Cristina Cavalcanti. Circuitos elétricos. São Paulo: Pearson Prentice Hall, c2006. xvi, 302 p. ISBN: 8576050722, 97885760507283.
- MARIOTTO, Paulo Antonio. Análise de circuitos elétricos. São Paulo: Prentice Hall, 2003. 378 p. ISBN: 8587918060.
- IRWIN, J. David. Análise de circuitos em engenharia. 4. ed. São Paulo: Makron Books, c2000. xvi, 848 p. ISBN: 8534606935.
- JOHNSON, David E., HILBURN, John L., JOHNSON, Johnny. R. Fundamentos de análise de circuitos elétricos. 4. ed. Rio de Janeiro: Prentice-Hall do Brasil, 1994. 539 p.
- DESOER, Charles A; KUH, Ernest S. Basic circuit theory. Tokyo: McGraw-Hill Kogakusha, 1969. xix, 876 p.
- HAYT, William Hart; KEMMERLY, Jack E. Jack Ellsworth. Análise de circuitos em engenharia. 7. ed. São Paulo: McGraw-Hill, c2008. 858 p. ISBN: 9788577260218.
